530. 二叉搜索树的最小绝对差

530. 二叉搜索树的最小绝对差

题目链接：530. 二叉搜索树的最小绝对差(简单)

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

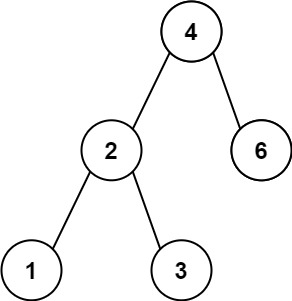
输入：root = [4,2,6,1,3]
输出：1

示例 2：

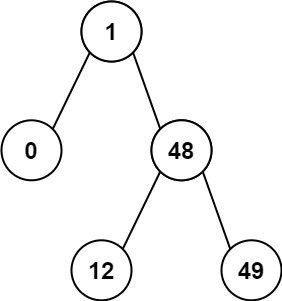
输入：root = [1,0,48,null,null,12,49]
输出：1

提示：

• 树中节点的数目范围是 [2, 104]

• 0 <= Node.val <= 105

解题思路

利用二叉搜索树的性质：二叉搜索树是有序的。

方法一：递归(借助一个数组)

将二叉树中序遍历的结果存放在一个数组中，再在这个数组上求两个相邻数的最小差值。

代码

C++

//递归，借助数组
class Solution {
public:
    vector<int> nodeVal;
    //中序遍历
    void traversal(TreeNode* root) {
        if (root == nullptr) return;
        traversal(root->left);
        nodeVal.push_back(root->val);
        traversal(root->right);
    }
    int getMinimumDifference(TreeNode* root) {
        nodeVal.clear();
        traversal(root);
        if (nodeVal.size() < 2) return 0;
        int subVal = nodeVal[nodeVal.size() - 1];
        for (int i = 1; i < nodeVal.size(); i++) {
            int sub = nodeVal[i] - nodeVal[i - 1];
            subVal = sub < subVal ? sub : subVal;
        }
        return subVal;
    }
};

JavaScript

//递归，数组辅助
var getMinimumDifference = function(root) {
    let nodeVal = [];
    const traversal = (cur) => {
        if (cur === null) return;
        traversal(cur.left);
        nodeVal.push(cur.val);
        traversal(cur.right);
    }
    traversal(root);
    let subVal = nodeVal[nodeVal.length - 1];
    for (let i = 1; i < nodeVal.length; i++) {
        var sub = nodeVal[i] - nodeVal[i - 1];
        subVal = sub < subVal ? sub : subVal;
    }
    return subVal;
};

方法二：递归

可以在对二叉搜索树中序遍历的过程中直接计算。用一个 pre 节点保存当前节点的上一个节点。

代码

C++

//递归，记录前一个节点
class Solution {
public:
    int subVal = INT_MAX;
    TreeNode* pre = nullptr; //记录前一个节点
    void traversal(TreeNode* root) {
        if (root == nullptr) return;
        traversal(root->left);
        if (pre != nullptr) {
            int sub = abs(root->val - pre->val);
            subVal = sub < subVal ? sub : subVal;
        }
        pre = root;
        traversal(root->right);
    }
    int getMinimumDifference(TreeNode* root) {
        traversal(root);
        return subVal;
    }
};

JavaScript

//直接递归
var getMinimumDifference = function(root) {
    let subVal = Infinity;
    let pre = null;
    const traversal = (cur) => {
        if (cur === null) return;
        traversal(cur.left);
        if (pre != null) {
            var sub = cur.val - pre.val;
            subVal = sub < subVal ? sub : subVal;
        }
        pre = cur;
        traversal(cur.right);
    }
    traversal(root);
    return subVal;
};

方法三：迭代

借助“栈”进行中序遍历的迭代，类似于二叉树的迭代遍历 和二叉树的统一迭代遍历 中的中序遍历。

代码

C++

//迭代(中序遍历)
class Solution {
public:
    int getMinimumDifference(TreeNode* root) {
       stack<TreeNode*> nodeSta;
       TreeNode* pre = nullptr; //记录前一个节点
       TreeNode* cur = root;
       int subVal = INT_MAX;
       while (cur != nullptr || !nodeSta.empty()) {
            if (cur != nullptr) {
                nodeSta.push(cur);
                cur = cur->left;
            } else {
                cur = nodeSta.top();
                nodeSta.pop();
                if (pre != nullptr) {
                    int sub = abs(cur->val - pre->val);
                    subVal = sub < subVal ? sub : subVal;
                }
                pre = cur;
                cur = cur->right;
            }
       }
       return subVal;
    }
};

JavaScript

//统一迭代
var getMinimumDifference = function(root) {
    let nodeVal = [];
    if (root != null) nodeVal.push(root);
    let subVal = Infinity;
    let pre = null;
    while (nodeVal.length != 0) {
        let node = nodeVal.pop();
        if (node != null) {
            if (node.right) nodeVal.push(node.right); //右
            nodeVal.push(node); //中
            nodeVal.push(null); //null
            if (node.left) nodeVal.push(node.left); //左
        } else {
            let cur = nodeVal.pop();
            if (pre != null) {
                var sub = cur.val - pre.val;
                subVal = sub < subVal ? sub : subVal;
            }
            pre = cur;
        }
    }
    return subVal;
};