98. 验证二叉搜索树
题目链接:
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
-
节点的左子树只包含 小于 当前节点的数。
-
节点的右子树只包含 大于 当前节点的数。
-
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
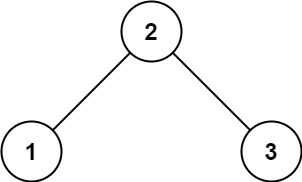
输入:root = [2,1,3]
输出:true
示例 2:
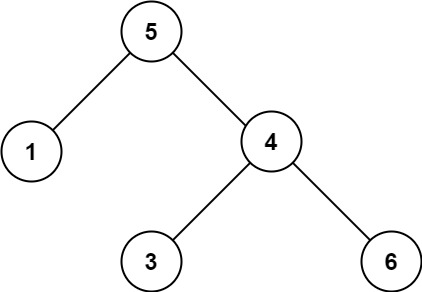
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
解题思路
易错点
一上来看到题目就开始写代码,这很简单嘛!殊不知掉进陷阱了~
//递归,但是有问题,这只能说明 根节点 大于 左子节点,小于 右子节点, //不能说明 根节点 大于 左子树的所有节点,小于 右子树的所有节点 class Solution1 { public: bool isValidBST(TreeNode* root) { if (root == nullptr) return true; if (root->left != nullptr && root->val <= root->left->val) return false; if (root->right!= nullptr && root->val >= root->right->val) return false; bool result1 = isValidBST(root->left); bool result2 = isValidBST(root->right); return result1 && result2; } };
上面的写法不能判断 根节点 大于 其左子树所有的节点,只能说明 根节点 大于 其左节点。同理也不能判断 根节点 小于 其右子树所有的节点,只能说明 根节点 小于 其右节点。
方法一:递归(借助一个数组)
二叉搜索树的特点是:将二叉搜索树进行中序遍历,并将遍历的结果存在数组中,那该数组一定是有序的(一般是递增的)。
所以可以按照叉搜索树的这一特征判断二叉树是否是二叉搜索树。
首先需要借助一个数组,然后对二叉树进行中序遍历并将遍历结果存入数组中,最后对数组进行判断。
代码
C++
//在中序遍历下,输出的二叉搜索树节点的数值是有序序列 class Solution { public: vector<int> valVec; //将二叉搜索树根据中序遍历转为数组 void traversal(TreeNode* root) { if (root == nullptr) return; traversal(root->left); //左 valVec.push_back(root->val); //中 traversal(root->right); //右 } bool isValidBST(TreeNode* root) { valVec.clear(); traversal(root); int value = valVec[0]; // 如果数组是单调递增的,则为二叉搜索树,否则不是 for (int i = 1; i < valVec.size(); i++) { if (value < valVec[i]) value = valVec[i]; else return false; } return true; } };
JavaScript
//辅助数组 let nums = []; function traversal(root) { if (root === null) return; traversal(root.left); nums.push(root.val); traversal(root.right); } var isValidBST = function(root) { nums = []; traversal(root); var value = nums[0]; for (var i = 1; i < nums.length; i++) { if (value >= nums[i]) return false; value = nums[i]; } return true; };
方法二:递归
不转变成数组,直接在递归遍历的过程中判断二叉树是否有序。
代码
C++
//在递归中直接判断二叉树是否是二叉搜索树(中序遍历) class Solution3 { public: TreeNode* pre = nullptr; //定义一个节点来保存先前节点 bool isValidBST(TreeNode* root) { if (root == nullptr) return true; bool leftResult = isValidBST(root->left); if (pre != nullptr && pre->val >= root->val) return false; pre = root; bool rightResult = isValidBST(root->right); return leftResult && rightResult; } };
JavaScript
/*****************该方法有问题****************************/ //记录前一个节点 let pre = null; var isValidBST = function(root) { if (root === null) return true; let leftResult = isValidBST(root.left); if (pre != null && pre.val >= root.val) return false; pre = root; // 记录前一个节点 let rightResult = isValidBST(root.right); return leftResult && rightResult; };
方法三:迭代
借助“栈”进行中序遍历的迭代,类似于
代码
C++
//统一迭代法(栈,中序遍历) class Solution4 { public: bool isValidBST(TreeNode* root) { stack<TreeNode*> nodeSta; if (root != nullptr) nodeSta.push(root); TreeNode* pre = nullptr; //记录前一个节点 while (!nodeSta.empty()) { TreeNode* node = nodeSta.top(); if (node != nullptr) { nodeSta.pop(); if (node->right) nodeSta.push(node->right); //右 nodeSta.push(node); //中 nodeSta.push(nullptr); //null if (node->left) nodeSta.push(node->left); //左 } else { nodeSta.pop(); if (pre != nullptr && pre->val >= nodeSta.top()->val) return false; pre = nodeSta.top(); nodeSta.pop(); } } return true; } }; //迭代法(栈,中序遍历) class Solution5 { public: bool isValidBST(TreeNode* root) { stack<TreeNode*> nodeSta; TreeNode* cur = root; TreeNode* pre = nullptr; //记录前一个节点 while (cur != nullptr || !nodeSta.empty()) { if (cur != nullptr) { nodeSta.push(cur); cur = cur->left; } else { cur = nodeSta.top(); nodeSta.pop(); if (pre != nullptr && pre->val >= cur->val) return false; pre = cur; cur = cur->right; } } return true; } };
JavaScript
//迭代法 var isValidBST = function(root) { let nodeSta = []; let cur = root; let pre = null; while(cur != null || nodeSta.length != 0) { if (cur != null) { nodeSta.push(cur); cur = cur.left; } else { cur = nodeSta.pop(); if (pre != null && pre.val >= cur.val) return false; pre = cur; cur = cur.right; } } return true; };



