654. 最大二叉树

654. 最大二叉树

题目链接：654. 最大二叉树(中等)

给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下：

1. 二叉树的根是数组 nums 中的最大元素。

2. 左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。

3. 右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。

返回有给定数组 nums 构建的 最大二叉树 。

示例 1：

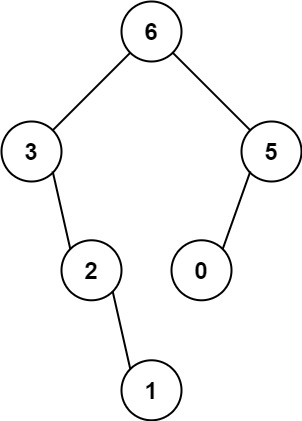
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

解题思路

与106. 从中序与后序遍历序列构造二叉树 类似，只是根节点是数组中的最大值。

代码

C++

class Solution {
public:
    unordered_map<int, int> numsMap;
    vector<int> Nums;
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        for (int i = 0; i < nums.size(); i++) {
            //将数组中的值和索引放入哈希表中
            numsMap[nums[i]] = i;
        }
        Nums = nums;
        return getTree(0, nums.size() - 1);
    }
​
    TreeNode* getTree(int s, int e) {
        if (s > e) return nullptr;
        //找出最大值
        int maxVal = Nums[s];
        for (int i = s; i <= e ; i++) {
            maxVal = Nums[i] > maxVal ? Nums[i] : maxVal;
        }
        int ri = numsMap[maxVal];
        TreeNode* node = new TreeNode(maxVal);
        node->left = getTree(s, ri - 1);
        node->right = getTree(ri + 1, e);
        return node;
    }
};

JavaScript

let numsMap = new Map();
let Nums = new Array();
​
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
var constructMaximumBinaryTree = function(nums) {
    for (var i = 0; i < nums.length; i++) {
        numsMap[nums[i]] = i;
    }
    Nums = nums;
    return getTree(0, nums.length - 1);
};
​
function getTree(s, e) {
    if (s > e) return null;
    var maxVal = Nums[s];
    for (var i = s; i <= e; i++) {
        maxVal = maxVal < Nums[i] ? Nums[i] : maxVal;
    }
    var ri = numsMap[maxVal];
    var node = new TreeNode(maxVal);
    node.left = getTree(s, ri - 1);
    node.right = getTree(ri + 1, e);
    return node;
}