572. 另一棵树的子树

572. 另一棵树的子树

题目链接：572. 另一棵树的子树(简单)

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

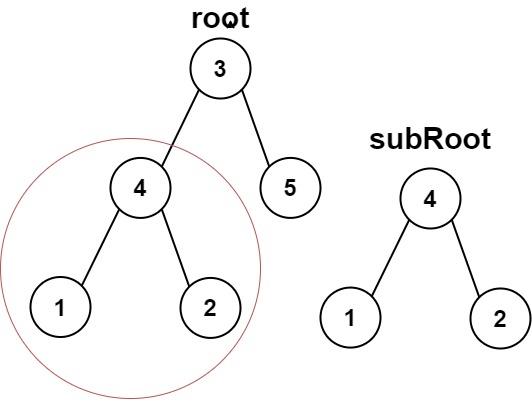
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

示例 2：

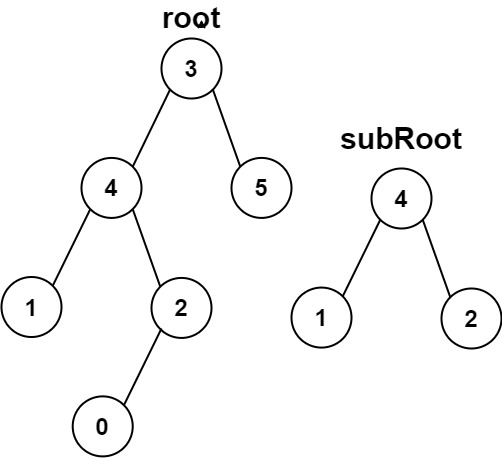
输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

题解

思路：该题与100. 相同的树 类似，即这道题就是在 root 的每个子节点上，判断由该子节点构成的子树是否和 subRoot 这颗树相等。判断两颗树相等需要同时满足三个条件：当前两颗树的根节点值相等；两颗树的左子树相等；两棵树的右子树相等。而判断 一棵树 是否为 另一颗树 的子树只需满足以下条件中的一个：当前两棵树相等；或 一棵树 是 另一颗树 的左子树；或 一棵树 是 另一棵树 的右子树。此题采用递归法求解。

代码(C++)：

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) { //判断两棵树是否相等
        if (p != nullptr && q == nullptr) return false;
        else if (p == nullptr && q != nullptr) return false;
        else if (p == nullptr && q == nullptr) return true;
        else if (p->val != q->val) return false;
        bool left = isSameTree(p->left, q->left); // 1号树：左、 2号树：左
        bool right = isSameTree(p->right, q->right); // 1号树：右、 2号树：右
        return left && right; // 1号树：中、 2号树：中 （逻辑处理）
    }
​
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if (subRoot == nullptr) return true;
        if (root == nullptr) return false;
        //判断 一棵树 是否为 另一棵树 的子树
        bool result1 = isSameTree(root, subRoot);
        bool result2 = isSubtree(root->left, subRoot);
        bool result3 = isSubtree(root->right, subRoot);
        return result1 || result2 || result3;
    }
};

代码(JavaScript)：

//递归法
var isSameTree = function(p, q) {
    if (p === null && q === null) return true;
    else if (p === null || q === null) return false;
    else if (p.val != q.val) return false;
​
    var result1 = isSameTree(p.left, q.left);
    var result2 = isSameTree(p.right, q.right);
    return result1 && result2;
​
};
var isSubtree = function(root, subRoot) {
    if (root === null && subRoot === null) return true;
    else if (root === null && subRoot != null) return false;
    var result1 = isSameTree(root, subRoot);
    var result2 = isSubtree(root.left, subRoot);
    var result3 = isSubtree(root.right, subRoot);
    return result1 || result2 || result3;
};