110. 平衡二叉树

110. 平衡二叉树

题目链接：110. 平衡二叉树(简单)

题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

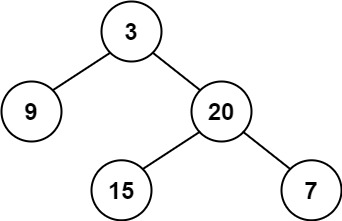
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

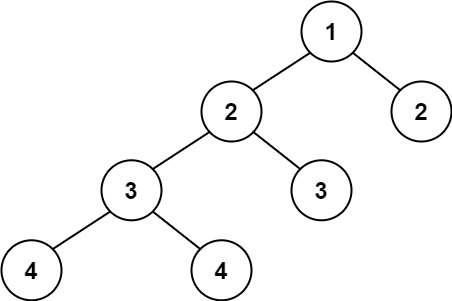
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

• 树中的节点数在范围 [0, 5000] 内

• -104 <= Node.val <= 104

题解

思路：首先弄清楚树中某一节点的高度和深度。此题中的高度和深度是按节点的个数来算的。

• 二叉树中节点的深度：指从根节点到该节点的最长简单路径边的条数(或节点的个数)。

• 二叉树中节点的高度：指从该节点到叶子节点的最长简单路径边的条数(或节点的个数)。

由此可见，求深度是从上到下的，所以使用前序遍历较合适。相反，求高度是从下到上的，所以使用后序遍历较合适。但是，对于二叉树中的根节点来说，根节点的高度就是二叉树的最大深度。

方法一：递归(后序遍历)

此题要求的是高度，所以采取后序遍历。

代码(C++)：

//递归：后序遍历
class Solution {
public:
    //1.递归函数的参数和返回值。参数：当前传入节点；返回值：以当前传入节点为根节点的树的高度
    int getHight(TreeNode* node){
        //2. 终止条件
        if (node == nullptr) return 0;
        // 不平衡的情况有3种：左树不平衡、右树不平衡、左树和右树差的绝对值大于1，这里用-1来标记此时已经不是一棵平衡二叉树了，就没必要往下继续走了。
        int leftHight = getHight(node->left);
        if (leftHight == -1) return -1;
        int rightHight = getHight(node->right);
        if (rightHight == -1) return -1;
        if(abs(leftHight - rightHight) > 1) return -1;
        else { // 如果都不是上述情况，说明平衡了，以当前传入节点为根节点的树的高度
            return max(leftHight, rightHight) + 1;
        }
    }
​
    bool isBalanced(TreeNode* root) {
        return getHight(root) == -1 ? false : true;
    }
};

代码(JavaScript)：

//递归(后序遍历)
function getHight(node) {
    if (node === null) return 0;
    var leftHight = getHight(node.left);
    if (leftHight === -1) return -1;
    var rightHight = getHight(node.right);
    if (rightHight === -1) return -1;
    if (Math.abs(leftHight - rightHight) > 1) return -1;
    else return Math.max(leftHight, rightHight) + 1;
}
var isBalanced = function(root) {
    return getHight(root) === -1 ? false : true;
};

方法二：迭代

虽然本题求的是高度，需要用后序遍历。但我们可以将当前传入节点看作是子树的根节点，那该子树的根节点的高度(最远叶子到根)就是该子树的最大深度(根到最远叶子)。那就可以用104. 二叉树的最大深度(层次遍历—使用队列迭代) 或104. 二叉树的最大深度(递归法) 来求出子树的高度。

但是迭代法会存在很多重复的计算，所以时间复杂度比较高。

代码(C++)：

//迭代：前序遍历+层次遍历
class Solution {
public:
    //将当前传入节点看作是子树的根节点，那该子树的根节点的高度(最远叶子到根)就是该子树的最大深度(根到最远叶子)
    //用层次遍历求最大深度
    int getDepth(TreeNode* node){
        queue<TreeNode*> que;
        if (node != nullptr) que.push(node);
        int maxlevel = 0;
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            maxlevel++;
        }
        return maxlevel;
    }
    //用栈来模拟前序遍历
    bool isBalanced(TreeNode* root) {
        stack<TreeNode*> sta;
        if(root != nullptr) sta.push(root);
        while (!sta.empty()) {
            TreeNode* node = sta.top();
            sta.pop();
            if (abs(getDepth(node->left) - getDepth(node->right)) > 1) return false;
            if(node->right) sta.push(node->right);
            if(node->left) sta.push(node->left);
        }
        return true;
    }
};

代码(JavaScript)：

//迭代(前序遍历+层次遍历)
function getDepth(node) {
    var que = new Array(); //队列
    if (node != null) que.push(node);
    var depth = 0;
    while (que.length != 0) {
        var size = que.length;
        for (var i = 0; i < size; i++) {
            var node1 = que.shift();
            if (node1.left) que.push(node1.left);
            if (node1.right) que.push(node1.right);
        }
        depth++;
    }
    return depth;
}
var isBalanced = function(root) {
    var sta = new Array(); //栈
    if (root != null) sta.push(root);
    while (sta.length != 0) {
        var node = sta.pop();
        if (Math.abs(getDepth(node.left) - getDepth(node.right)) > 1) return false;
        if (node.right) sta.push(node.right);
        if (node.left) sta.push(node.left);
    }
    return true;
};