222. 完全二叉树的节点个数

222. 完全二叉树的节点个数

题目链接：222. 完全二叉树的节点个数(中等)

题目描述

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

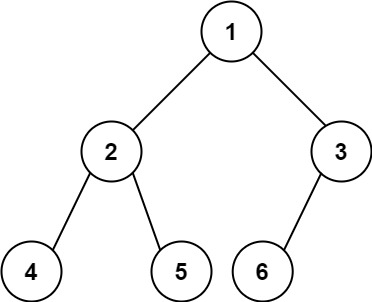
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1 

提示：

• 树中节点的数目范围是[0, 5 * 104]

• 0 <= Node.val <= 5 * 104

• 题目数据保证输入的树是 完全二叉树

进阶：遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

题解

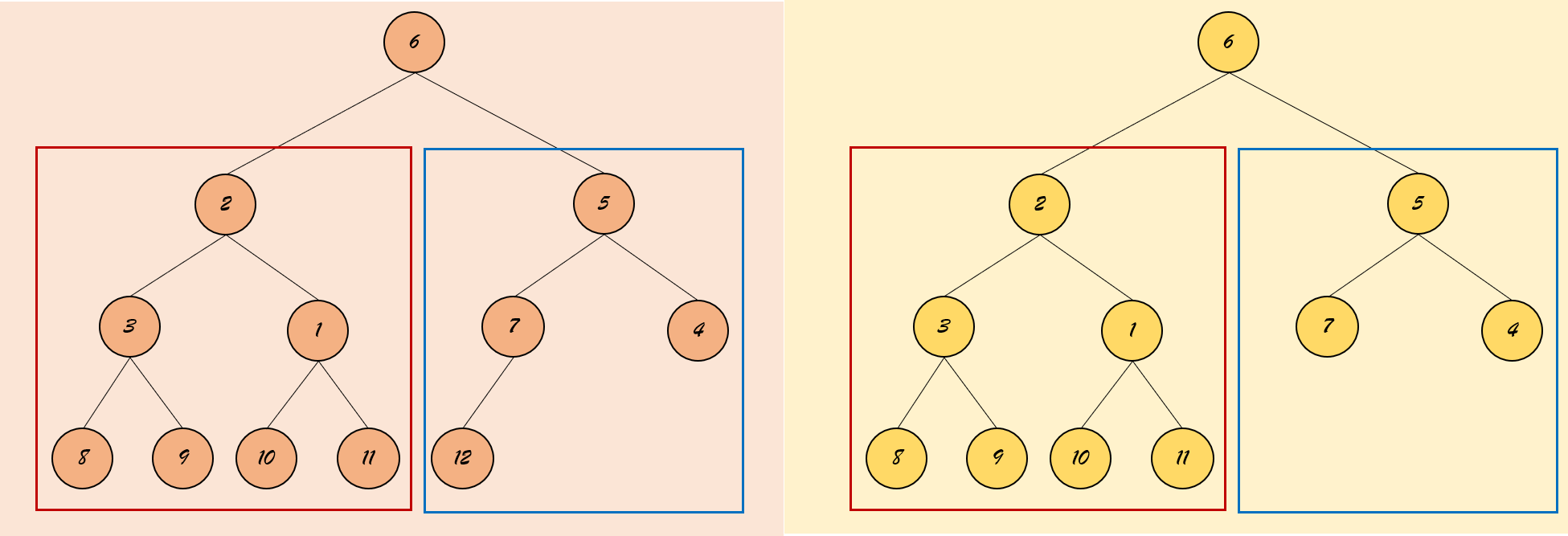
思路：不考虑”进阶“，完全二叉树就是一棵二叉树，求节点的个数和遍历节点类似。但由于完全二叉树的特殊性。由下图我们可以发现：如果左子树的深度等于右子树的深度，则左子树为满二叉树；如果左子树的深度大于右子树的深度，则右子树为满二叉树。

代码(C++)：

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int value) : val(value), left(nullptr), right(nullptr) {}
};
​
​
class Solution1 {
public:
    //按照一般的二叉树来求，有递归法和迭代法
    //方法一：后序遍历(递归法)
    int countNodes(TreeNode* root) {
        if (root == nullptr) return 0;
        int leftNums = countNodes(root->left);
        int rightNums = countNodes(root->right);
        int nums =leftNums + rightNums + 1;
        return nums;
    }
};
​
class Solution2 {
public:
    //按照一般的二叉树来求，有递归法和迭代法
    //方法二：层次遍历(迭代法)
    int countNodes(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != nullptr) que.push(root);
        int nums = 0;
        while (!que.empty()) {
           TreeNode* node = que.front();
           que.pop();
           nums++;
           if (node->left) que.push(node->left);
           if (node->right) que.push(node->right);
        }
        return nums;
    }
};
​
class Solution3 {
public:
    //完全二叉树是特殊的二叉树
    //方法三：
    int getDepth (TreeNode* node) {
        int depth = 0;
        while (node) {
            depth++;
            node = node->left;
        }
        return depth;
    }
    int countNodes(TreeNode* root) {
        if (root == nullptr) return 0;
        // 以根节点分成左子树和右子树，分别求他们的深度
        int leftDepth = getDepth(root->left);
        int rightDepth = getDepth(root->right);
​
        if (leftDepth == rightDepth) {
            return countNodes(root->right) + (pow(2,leftDepth) - 1) + 1;
        } else {
            return (pow(2,rightDepth) - 1 ) + countNodes(root->left) + 1;
        }
    }
};

代码(JavaScript)：

//构造函数
function TreeNode(val, left, right) {
    this.val = (val === undefined ? 0 : val);
    this.left = (left === undefined ? null : left);
    this.right = (right == undefined ? null : right);
}
​
var root = new TreeNode();
​
//方法一：递归法(后序遍历)
var countNodes = function(root) {
    if (root === null) return 0;
    var leftNums = countNodes(root.left);
    var rightNums = countNodes(root.right);
    return rightNums + leftNums + 1;
};
​
//方法二：迭代法(层次遍历)
var countNodes1 = function(root) {
    var que = new Array();
    if (root != null) que.push(root);
    var Nums = 0;
    while (que.length != 0) {
        var node = que.shift();
        Nums++;
        if (node.left) que.push(node.left);
        if (node.right) que.push(node.right);
    }
    return Nums;
};
​
​
//方法三：利用二叉树的性质
function getDepth(node) {
    var depth = 0;
    while (node) {
        depth++;
        node = node.left;
    }
    return depth;
}
​
var countNodes2 = function(root) {
    if (root === null) return 0;
    var leftDepth = getDepth(root.left);
    var rightDepth = getDepth(root.right);
    if (leftDepth === rightDepth) {
        return countNodes(root.right) + (Math.pow(2, leftDepth) - 1) + 1;
    } else {
        return (Math.pow(2, rightDepth) - 1) + countNodes(root.left) + 1;
    }
};

分析：

普通二叉树的方法(方法一，方法二)

• 时间复杂度：O(N)，N是树的节点个数

• 空间复杂度：方法一(O(logN))，递归中栈的开销；方法二(O(N))，迭代中队列的开销；

满二叉树(方法三)

• 时间复杂度：O(logN * logN)

• 空间复杂度：O(logN )