239. 滑动窗口最大值
题目链接：
题目描述
给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
示例 1：
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2：
输入：nums = [1], k = 1
输出：[1]
示例 3：
输入：nums = [1,-1], k = 1
输出：[1,-1]
示例 4：
输入：nums = [9,11], k = 2
输出：[11]
示例 5：
输入：nums = [4,-2], k = 2
输出：[4]
提示：
-
1 <= nums.length <= 105
-
-104 <= nums[i] <= 104
-
1 <= k <= nums.length
题解
思路：实现滑动窗口并不难，难就难在如何得到滑动窗口里面的最大值。如何使用暴力的方案，比较每个窗口里面的所有元素，则时间复杂度将是O(N*K)。所以我们采用单调队列，其中的元素保证是单调递减的，这样队头元素就是我们要找的最大值了。但需要保证队列里面的元素是当前的窗口值。下图展示了两个不同的案例。
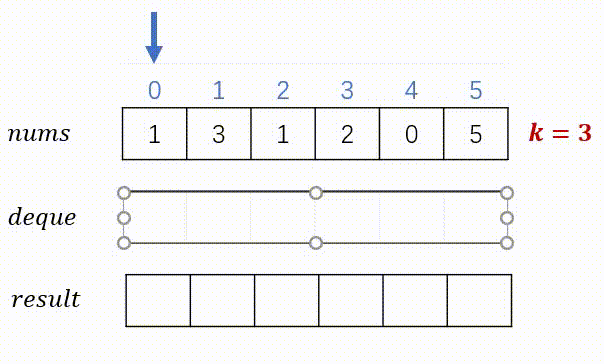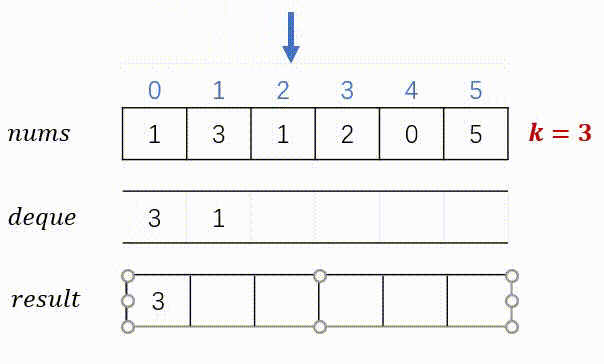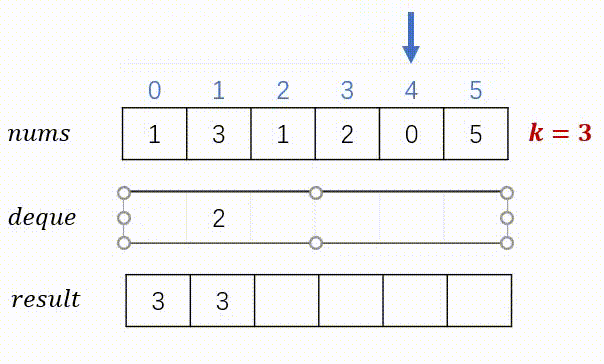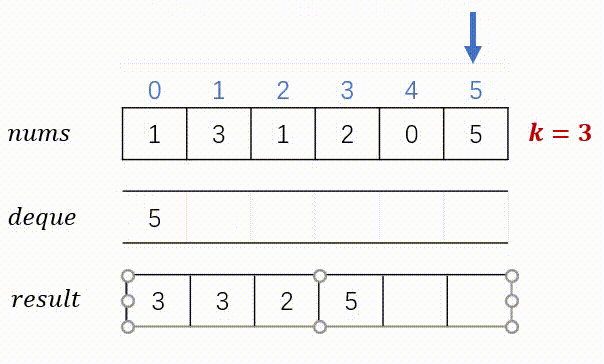
代码(C++)
vector<int> maxSlidingWindow(vector<int>& nums, int k) { deque<int> que;//从大到小的单调队列 vector<int> result; //先将前面 k 个元素放入队列中，注意要保持单调队列的特性（从大到小） for (int i = 0; i < k; i++) { //弹出队列中小于 nums[i] 的元素 while (!que.empty() && nums[i] > que.back()) { que.pop_back(); } //将 nums[i] 放到队列中的合适位置 que.push_back(nums[i]); } //将一开始的 k 个元素的最大值存入 result result.push_back(que.front()); //滑动窗口，每次滑动一个位置 for (int i = k; i < nums.size(); i++) { //如果队列中的第一个元素并不属于当前的滑动窗口，需弹出 if (nums[i - k] == que.front()) { que.pop_front(); } //如果队列不为空，则需要移除队列当中比nums[i]小的元素 while (!que.empty() && nums[i] > que.back()) { que.pop_back(); } //将 nums[i] 放到队列中的合适位置 que.push_back(nums[i]); //此时队列中的第一个元素即为最大值，存入 result result.push_back(que.front()); } return result; }
分析：
-
时间复杂度：O(N)， N 是数组nums 的长度。因为数组中的每个元素恰好被放入队列一次，并且最多被弹出队列一次。
-
空间复杂度：O(K)。我们使用的数据结构是双向队列，”不断从队首弹出元素“保证了队列中最多不会有超过 k+1个元素。
简化代码：
vector<int> maxSlidingWindow(vector<int>& nums, int k) { deque<int> que;//从大到小的单调队列 vector<int> result; for (int i = 0; i < nums.size(); i++) { while (!que.empty() && nums[i] > que.back()) { que.pop_back(); } que.push_back(nums[i]); if (i >= k && nums[i - k] == que.front()) { que.pop_front(); } if (i >= k - 1) { result.push_back(que.front()); } } return result; }
参考链接
