209. 长度最小的子数组

题目：https://leetcode-cn.com/problems/minimum-size-subarray-sum/

自己写的代码：

C++版本：
int minSubArrayLen(int target, vector<int>& nums) {
    if(nums.size() == 0) return 0;
    int len = INT_MAX;
    int tmplen = 0;
    for(int i = 0; i < nums.size(); i++){
        int j = i;
        int tmp = 0;
        while (tmp < target && j < nums.size()){
            tmp += nums[j];
            tmplen = j - i;
            j++;
        }
        if (tmp >= target && tmplen < len){
            len = tmplen + 1;
        }
    }
    return len == INT_MAX ? 0 : len; //len等于INT_MAX就输出0，len不等于INT_MAX就输出len。
}

知识点：

1、INT_MAX和INT_MIN： https://blog.csdn.net/weixin_40539125/article/details/86032914

大多数时候，在竞争性编程中，需要分配数据类型可以容纳的变量，最大值或最小值，但是记住如此大而精确的数字是一项困难的工作。因此，C ++有一些宏来表示这些数字，因此可以直接将这些宏分配给变量，而无需实际输入整数。

INT_MAX是一个宏，指定整数变量不能存储超出此限制的任何值。
INT_MIN指定整数变量不能存储低于此限制的任何值。

INT_MAX和INT_MIN的值可能不同，
从编译器到编译器。以下是编译器中整数的典型值，
使用32位存储。

INT_MAX的值为+2147483647。
INT_MIN的值为-2147483648。

JAVA版本：    
  public static int minSubArrayLen(int target, int[] nums) {
        if(nums.length == 0) return 0;
        int len = Integer.MAX_VALUE;;
        int tmplen = 0;
        for(int i = 0; i < nums.length; i++){
            int j = i;
            int tmp = 0;
            while (tmp < target && j < nums.length){
                tmp += nums[j];
                tmplen = j - i;
                j++;
            }
            if (tmp >= target && tmplen < len){
                len = tmplen + 1;
            }
        }
        return len == Integer.MAX_VALUE ? 0 : len;
   }

 

代码随想录：https://programmercarl.com/0209.%E9%95%BF%E5%BA%A6%E6%9C%80%E5%B0%8F%E7%9A%84%E5%AD%90%E6%95%B0%E7%BB%84.html#_209-%E9%95%BF%E5%BA%A6%E6%9C%80%E5%B0%8F%E7%9A%84%E5%AD%90%E6%95%B0%E7%BB%84

暴力解法（我的方法也属于暴力破解）

这道题目暴力解法当然是 两个for循环，然后不断的寻找符合条件的子序列，时间复杂度很明显是O(n^2) 。

C++版本：
class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX; // 最终的结果
        int sum = 0; // 子序列的数值之和
        int subLength = 0; // 子序列的长度
        for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
            sum = 0;
            for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
                sum += nums[j];
                if (sum >= s) { // 一旦发现子序列和超过了s，更新result
                    subLength = j - i + 1; // 取子序列的长度
                    result = result < subLength ? result : subLength;
                    break; // 因为我们是找符合条件最短的子序列，所以一旦符合条件就break
                }
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

时间复杂度：$O(n^2)$ 空间复杂度：$O(1) 

滑动窗口

接下来就开始介绍数组操作中另一个重要的方法：滑动窗口。

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

这里还是以题目中的示例来举例，s=7， 数组是 2，3，1，2，4，3，来看一下查找的过程：

 

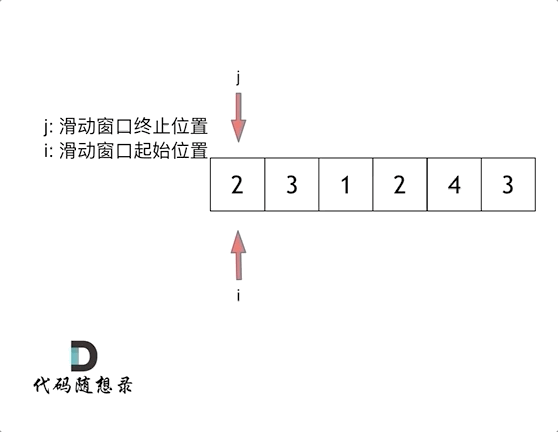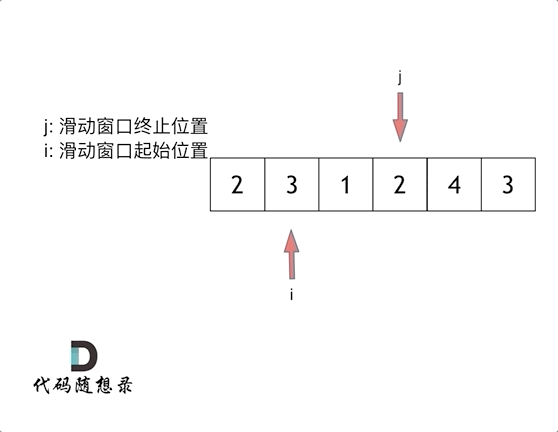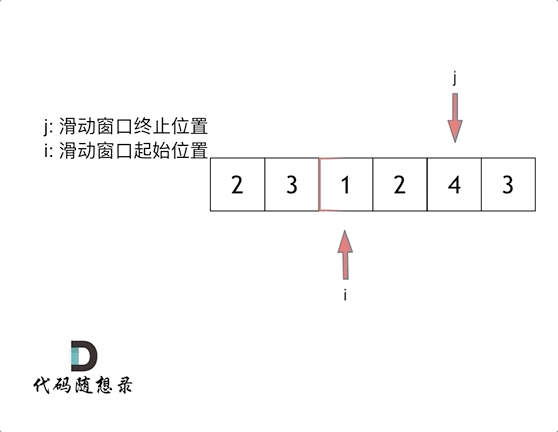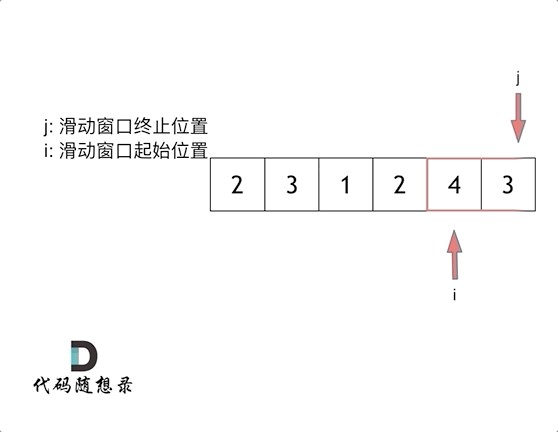
最后找到 4，3 是最短距离。

其实从动画中可以发现滑动窗口也可以理解为双指针法的一种！只不过这种解法更像是一个窗口的移动，所以叫做滑动窗口更适合一些。

在本题中实现滑动窗口，主要确定如下三点：

• 窗口内是什么？
• 如何移动窗口的起始位置？
• 如何移动窗口的结束位置？

窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。

窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。

窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，窗口的起始位置设置为数组的起始位置就可以了。

解题的关键在于 窗口的起始位置如何移动，如图所示：

 

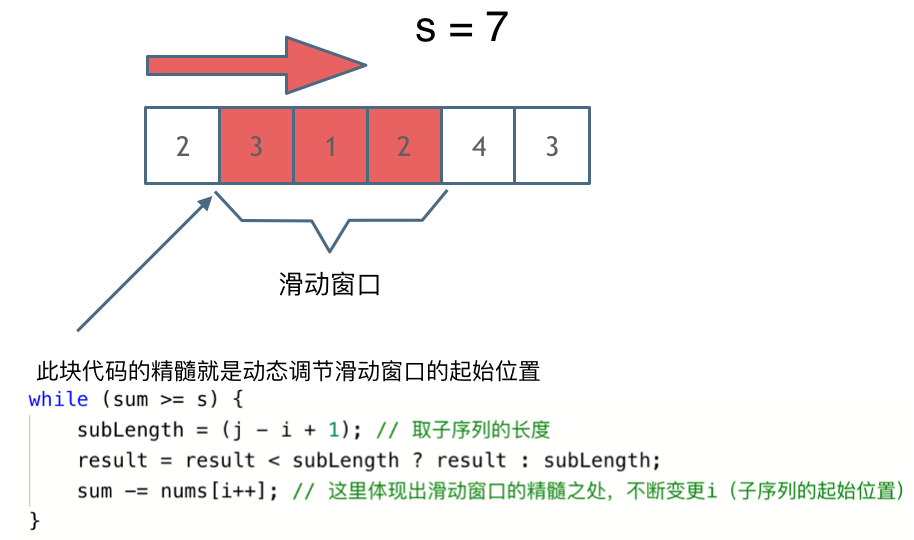
可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。

C++版本：
class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX;
        int sum = 0; // 滑动窗口数值之和
        int i = 0; // 滑动窗口起始位置
        int subLength = 0; // 滑动窗口的长度
        for (int j = 0; j < nums.size(); j++) {
            sum += nums[j];
            // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
            while (sum >= s) {
                subLength = (j - i + 1); // 取子序列的长度
                result = result < subLength ? result : subLength;
                sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

时间复杂度：$O(n)$
空间复杂度：$O(1)$

一些录友会疑惑为什么时间复杂度是O(n)。不要以为for里放一个while就以为是$O(n^2)$啊， 主要是看每一个元素被操作的次数，每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被被操作两次，所以时间复杂度是2 * n 也就是$O(n)$。

JAVA版本：
class Solution {
    // 滑动窗口
    public int minSubArrayLen(int s, int[] nums) {
        int left = 0;
        int sum = 0;
        int result = Integer.MAX_VALUE;
        for (int right = 0; right < nums.length; right++) {
            sum += nums[right];
            while (sum >= s) {
                result = Math.min(result, right - left + 1);
                sum -= nums[left++];
            }
        }
        return result == Integer.MAX_VALUE ? 0 : result;
    }
}

 

官网：https://leetcode-cn.com/problems/minimum-size-subarray-sum/solution/chang-du-zui-xiao-de-zi-shu-zu-by-leetcode-solutio/

方法一：暴力法

暴力法是最直观的方法。初始化子数组的最小长度为无穷大，枚举数组nums 中的每个下标作为子数组的开始下标，对于每个开始下标 i，需要找到大于或等于 i 的最小下标 j，使得从 nums[i] 到 nums[j] 的元素和大于或等于 s，并更新子数组的最小长度（此时子数组的长度是 j−i+1）。

 C++版本：
   int minSubArrayLen(int s, vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int ans = INT_MAX;
        for (int i = 0; i < n; i++) {
            int sum = 0;
            for (int j = i; j < n; j++) {
                sum += nums[j];
                if (sum >= s) {
                    ans = min(ans, j - i + 1);
                    break;
                }
            }
        }
        return ans == INT_MAX ? 0 : ans;
    }

JAVA版本：
public int minSubArrayLen(int s, int[] nums) {
        int n = nums.length;
        if (n == 0) {
            return 0;
        }
        int ans = Integer.MAX_VALUE;
        for (int i = 0; i < n; i++) {
            int sum = 0;
            for (int j = i; j < n; j++) {
                sum += nums[j];
                if (sum >= s) {
                    ans = Math.min(ans, j - i + 1);
                    break;
                }
            }
        }
        return ans == Integer.MAX_VALUE ? 0 : ans;
    }

复杂度分析

时间复杂度：O(n^2)，其中 n 是数组的长度。需要遍历每个下标作为子数组的开始下标，对于每个开始下标，需要遍历其后面的下标得到长度最小的子数组。

空间复杂度：O(1)。

方法二：前缀和 + 二分查找

方法一的时间复杂度是O(n^2)，因为在确定每个子数组的开始下标后，找到长度最小的子数组需要 O(n) 的时间。如果使用二分查找，则可以将时间优化到 O(logn)。

为了使用二分查找，需要额外创建一个数组 sums 用于存储数组nums 的前缀和，其中 sums[i] 表示从 nums[0] 到 nums[i−1] 的元素和。得到前缀和之后，对于每个开始下标 i，可通过二分查找得到大于或等于 i 的最小下标 bound，使得 sums[bound]−sums[i−1]≥s，并更新子数组的最小长度（此时子数组的长度是bound−(i−1)）。

因为这道题保证了数组中每个元素都为正，所以前缀和一定是递增的，这一点保证了二分的正确性。如果题目没有说明数组中每个元素都为正，这里就不能使用二分来查找这个位置了。

在很多语言中，都有现成的库和函数来为我们实现这里二分查找大于等于某个数的第一个位置的功能，比如 C++ 的 lower_bound，Java 中的 Arrays.binarySearch，C# 中的 Array.BinarySearch，Python 中的 bisect.bisect_left。但是有时面试官可能会让我们自己实现一个这样的二分查找函数，这里给出一个 C# 的版本，供读者参考：

C#版本：
private int LowerBound(int[] a, int l, int r, int target) 
{
    int mid = -1, originL = l, originR = r;
    while (l < r) 
    {
        mid = (l + r) >> 1;
        if (a[mid] < target) l = mid + 1;
        else r = mid;
    } 

    return (a[l] >= target) ? l : -1;
}

下面是这道题的代码。

C++版本：
int minSubArrayLen(int s, vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int ans = INT_MAX;
        vector<int> sums(n + 1, 0); 
        // 为了方便计算，令 size = n + 1 
        // sums[0] = 0 意味着前 0 个元素的前缀和为 0
        // sums[1] = A[0] 前 1 个元素的前缀和为 A[0]
        // 以此类推
        for (int i = 1; i <= n; i++) {
            sums[i] = sums[i - 1] + nums[i - 1];
        }
        for (int i = 1; i <= n; i++) {
            int target = s + sums[i - 1];
            auto bound = lower_bound(sums.begin(), sums.end(), target);
            if (bound != sums.end()) {
                ans = min(ans, static_cast<int>((bound - sums.begin()) - (i - 1)));
            }
        }
        return ans == INT_MAX ? 0 : ans;
    }

JAVA版本：
public int minSubArrayLen(int s, int[] nums) {
        int n = nums.length;
        if (n == 0) {
            return 0;
        }
        int ans = Integer.MAX_VALUE;
        int[] sums = new int[n + 1]; 
        // 为了方便计算，令 size = n + 1 
        // sums[0] = 0 意味着前 0 个元素的前缀和为 0
        // sums[1] = A[0] 前 1 个元素的前缀和为 A[0]
        // 以此类推
        for (int i = 1; i <= n; i++) {
            sums[i] = sums[i - 1] + nums[i - 1];
        }
        for (int i = 1; i <= n; i++) {
            int target = s + sums[i - 1];
            int bound = Arrays.binarySearch(sums, target);
            if (bound < 0) {
                bound = -bound - 1;
            }
            if (bound <= n) {
                ans = Math.min(ans, bound - (i - 1));
            }
        }
        return ans == Integer.MAX_VALUE ? 0 : ans;
    }

复杂度分析

时间复杂度：O(nlogn)，其中 n 是数组的长度。需要遍历每个下标作为子数组的开始下标，遍历的时间复杂度是O(n)，对于每个开始下标，需要通过二分查找得到长度最小的子数组，二分查找得时间复杂度是 O(logn)，因此总时间复杂度是 O(nlogn)。

空间复杂度：O(n)，其中 n 是数组的长度。额外创建数组 sums 存储前缀和。

方法三：滑动窗口
在方法一和方法二中，都是每次确定子数组的开始下标，然后得到长度最小的子数组，因此时间复杂度较高。为了降低时间复杂度，可以使用滑动窗口的方法。

定义两个指针start 和 end 分别表示子数组（滑动窗口窗口）的开始位置和结束位置，维护变量 sum 存储子数组中的元素和（即从nums[start] 到 nums[end] 的元素和）。

初始状态下，start 和 end 都指向下标 0，sum 的值为 0。

每一轮迭代，将 nums[end] 加到 sum，如果 sum≥s，则更新子数组的最小长度（此时子数组的长度是 end−start+1），然后将 nums[start] 从sum 中减去并将 start 右移，直到 sum<s，在此过程中同样更新子数组的最小长度。在每一轮迭代的最后，将 end 右移。

C++版本：
    int minSubArrayLen(int s, vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int ans = INT_MAX;
        int start = 0, end = 0;
        int sum = 0;
        while (end < n) {
            sum += nums[end];
            while (sum >= s) {
                ans = min(ans, end - start + 1);
                sum -= nums[start];
                start++;
            }
            end++;
        }
        return ans == INT_MAX ? 0 : ans;
    }

JAVA版本：
    public int minSubArrayLen(int s, int[] nums) {
        int n = nums.length;
        if (n == 0) {
            return 0;
        }
        int ans = Integer.MAX_VALUE;
        int start = 0, end = 0;
        int sum = 0;
        while (end < n) {
            sum += nums[end];
            while (sum >= s) {
                ans = Math.min(ans, end - start + 1);
                sum -= nums[start];
                start++;
            }
            end++;
        }
        return ans == Integer.MAX_VALUE ? 0 : ans;
    }

复杂度分析

时间复杂度：O(n)，其中 n 是数组的长度。指针 start 和 end 最多各移动 n 次。

空间复杂度：O(1)。

 

精选解法：https://leetcode-cn.com/problems/minimum-size-subarray-sum/solution/javade-jie-fa-ji-bai-liao-9985de-yong-hu-by-sdwwld/

2.使用队列相加（实际上我们也可以把它称作是滑动窗口，这里的队列其实就相当于一个窗口）
我们把数组中的元素不停的入队，直到总和大于等于 s 为止，接着记录下队列中元素的个数，然后再不停的出队，直到队列中元素的和小于 s 为止（如果不小于 s，也要记录下队列中元素的个数，这个个数其实就是不小于 s 的连续子数组长度，我们要记录最小的即可）。接着再把数组中的元素添加到队列中……重复上面的操作，直到数组中的元素全部使用完为止。
这里以 [2,3,1,2,4,3] 举例画个图来看下

 

 

 

 

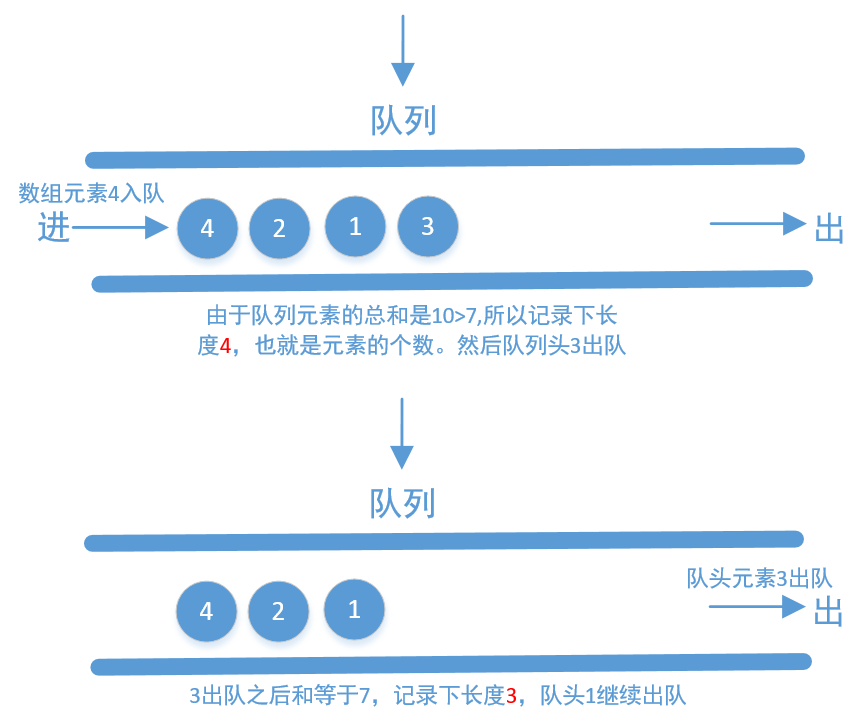
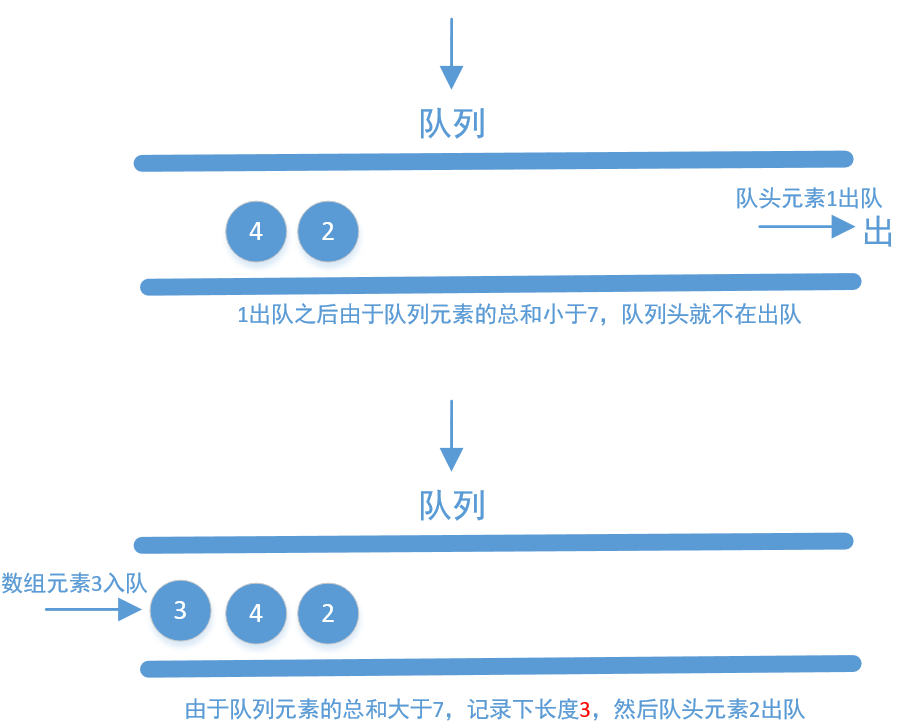
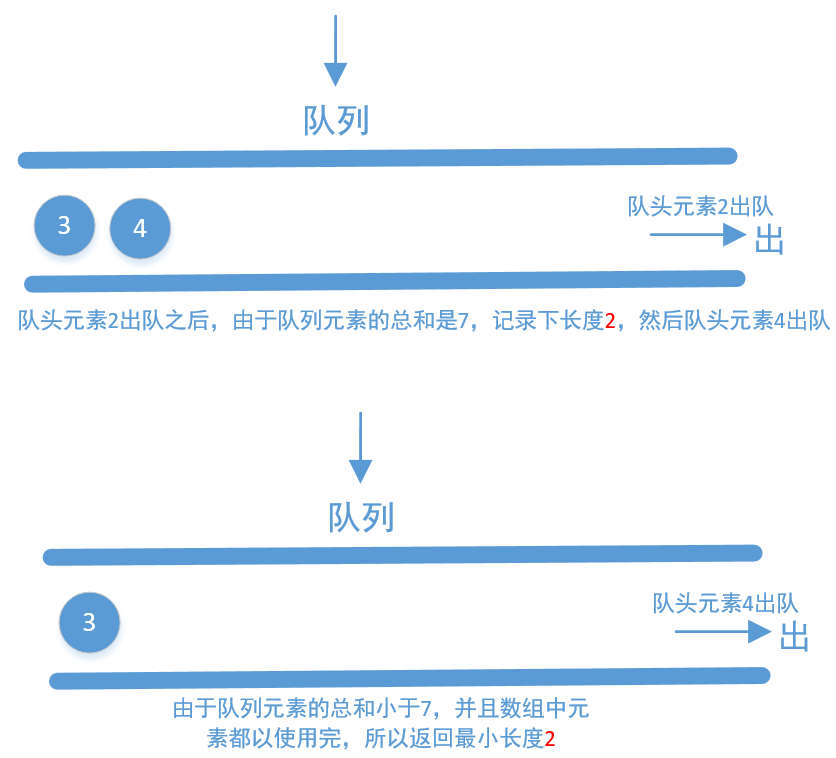
上面画的是使用队列，但在代码中我们不直接使用队列，我们使用两个指针，一个指向队头一个指向队尾，我们来看下代码

JAVA版本：    
    public int minSubArrayLen(int s, int[] nums) {
        int lo = 0, hi = 0, sum = 0, min = Integer.MAX_VALUE;
        while (hi < nums.length) {
            sum += nums[hi++];
            while (sum >= s) {
                min = Math.min(min, hi - lo);
                sum -= nums[lo++];
            }
        }
        return min == Integer.MAX_VALUE ? 0 : min;
    }

3.使用队列相减

第一种是使用相加的方式，这里我们改为相减的方式，基本原理都差不多，

JAVA版本：
 public int minSubArrayLen(int s, int[] nums) {
        int lo = 0, hi = 0, min = Integer.MAX_VALUE;
        while (hi < nums.length) {
            s -= nums[hi++];
            while (s <= 0) {
                min = Math.min(min, hi - lo);
                s += nums[lo++];
            }
        }
        return min == Integer.MAX_VALUE ? 0 : min;
    }

4.二分法查找
我们申请一个临时数组 sums，其中 sums[i] 表示的是原数组 nums 前 i 个元素的和，题中说了 “给定一个含有 n 个 正整数 的数组”，既然是正整数，那么相加的和会越来越大，也就是sums数组中的元素是递增的。我们只需要找到 sums[k]-sums[j]>=s，那么 k-j 就是满足的连续子数组，但不一定是最小的，所以我们要继续找，直到找到最小的为止。怎么找呢，我们可以使用两个 for 循环来枚举，但这又和第一种暴力求解一样了，所以我们可以换种思路，求 sums[k]-sums[j]>=s 我们可以求 sums[j]+s<=sums[k]，那这样就好办了，因为数组sums中的元素是递增的，也就是排序的，我们只需要求出 sum[j]+s 的值，然后使用二分法查找即可找到这个 k。

JAVA版本：
    public int minSubArrayLen(int s, int[] nums) {
        int length = nums.length;
        int min = Integer.MAX_VALUE;
        int[] sums = new int[length + 1];
        for (int i = 1; i <= length; i++) {
            sums[i] = sums[i - 1] + nums[i - 1];
        }
        for (int i = 0; i <= length; i++) {
            int target = s + sums[i];
            int index = Arrays.binarySearch(sums, target);
            if (index < 0)
                index = ~index;
            if (index <= length) {
                min = Math.min(min, index - i);
            }
        }
        return min == Integer.MAX_VALUE ? 0 : min;
    }

注意这里的函数 int index = Arrays.binarySearch(sums, target);如果找到就会返回值的下标，如果没找到就会返回一个负数，这个负数取反之后就是查找的值应该在数组中的位置
举个例子，比如排序数组 [2，5，7，10，15，18，20] 如果我们查找 18，因为有这个数会返回 18 的下标 5，如果我们查找 9，因为没这个数会返回 -4（至于这个是怎么得到的，大家可以看下源码，这里不再过多展开讨论），我们对他取反之后就是3，也就是说如果我们在数组中添加一个 9，他在数组的下标是 3，也就是第 4 个位置（也可以这么理解，只要取反之后不是数组的长度，那么他就是原数组中第一个比他大的值的下标）

5.直接使用窗口
上面第 2 种解法我们使用的是使用两个指针，我们也可以把它看做是一个窗口，每次往窗口中添加元素来判断是否满足。其实我们可以逆向思维，先固定一个窗口大小比如 leng，然后遍历数组，查看在数组中 leng 个元素长度的和是否有满足的，如果没有满足的我们就扩大窗口的大小继续查找，如果有满足的我们就记录下窗口的大小 leng，因为这个 leng 不一定是最小的，我们要缩小窗口的大小再继续找……

JAVA版本：
    public int minSubArrayLen(int s, int[] nums) {
        int lo = 1, hi = nums.length, min = 0;
        while (lo <= hi) {
            int mid = (lo + hi) >> 1;
            if (windowExist(mid, nums, s)) {
                hi = mid - 1;//找到就缩小窗口的大小
                min = mid;//如果找到就记录下来
            } else
                lo = mid + 1;//没找到就扩大窗口的大小
        }
        return min;
    }

    //size窗口的大小
    private boolean windowExist(int size, int[] nums, int s) {
        int sum = 0;
        for (int i = 0; i < nums.length; i++) {
            if (i >= size)
                sum -= nums[i - size];
            sum += nums[i];
            if (sum >= s)
                return true;
        }
        return false;
    }