28. 实现 strStr()

题目：https://leetcode-cn.com/problems/implement-strstr/

自己的解答：

    public int strStr(String haystack, String needle) {
        int p=-1;
        String b="";
        if(needle.equals("")){
            return 0;
        }else{
            b=needle.substring(0,1);
        }
        for(int i=0;i<haystack.length();i++){
            String a=haystack.substring(i,i+1);
            if(a.equals(b) && (haystack.length()-i)>=needle.length()){
                String s=haystack.substring(i,(i+needle.length()));
                if(s.equals(needle)){
                    return i;
                }
            }
        }
        return p;
    }

注意：在字符串进行比较时一定要用 ".equals()" 

 

官方解答：https://leetcode-cn.com/problems/implement-strstr/solution/shi-xian-strstr-by-leetcode-solution-ds6y/

本题是经典的字符串单模匹配的模型，因此可以使用字符串匹配算法解决，常见的字符串匹配算法包括暴力匹配、Knuth-Morris-Pratt 算法、Boyer-Moore 算法、Sunday 算法等，本文将讲解 Knuth-Morris-Pratt 算法。因为哈希方法可能出现哈希值相等但是字符串不相等的情况，而 strStr 函数要求匹配结果必定正确，因此本文不介绍哈希方法，有兴趣的读者可以自行了解滚动哈希的实现（如 Rabin-Karp 算法）。

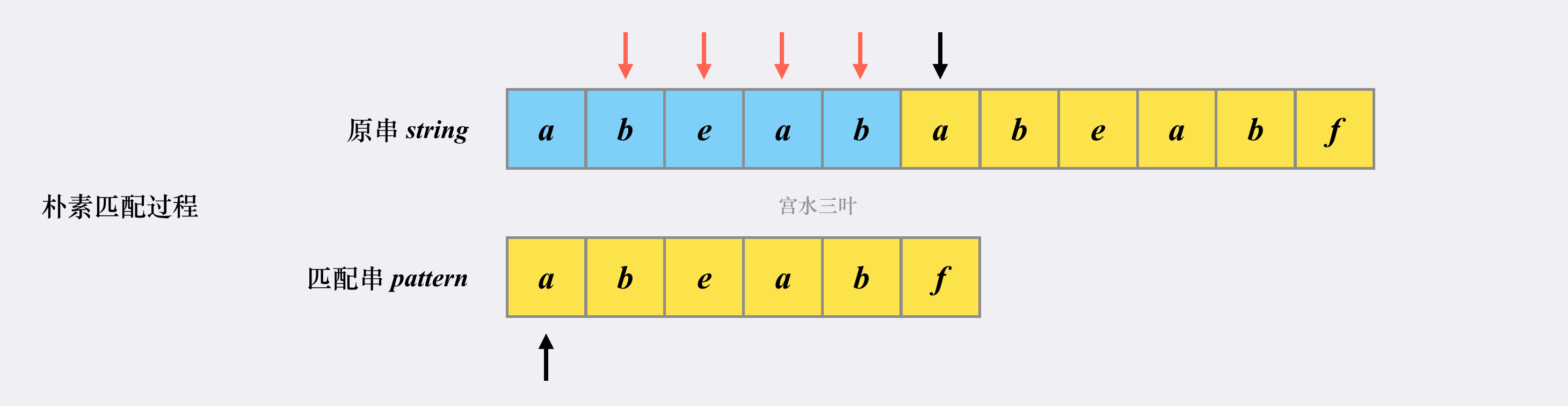
方法1：暴力匹配。

思路及算法：我们可以让字符串 needle 与字符串 haystack 的所有长度为 m 的子串均匹配一次。为了减少不必要的匹配，我们每次匹配失败即立刻停止当前子串的匹配，对下一个子串继续匹配。如果当前子串匹配成功，我们返回当前子串的开始位置即可。如果所有子串都匹配失败，则返回 −1。

public int strStr(String haystack, String needle) {
        int n = haystack.length(), m = needle.length();
        for (int i = 0; i + m <= n; i++) {
            boolean flag = true;
            for (int j = 0; j < m; j++) {
                if (haystack.charAt(i + j) != needle.charAt(j)) {
                    flag = false;
                    break;
                }
            }
            if (flag) {
                return i;
            }
        }
        return -1;
    }

知识点：

1、java中break和continue的用法

• break用于switch语句中，终止switch语句
• break用于循环时，跳出循环
• break用于其他位置，毫无意义
• continue用在循环中，跳出本次循环，继续执行下一次循环
• continue用在其他地方毫无意义

2、public char charAt(int index)：用于返回指定索引处的字符。索引范围为从 0 到 length() - 1。

 

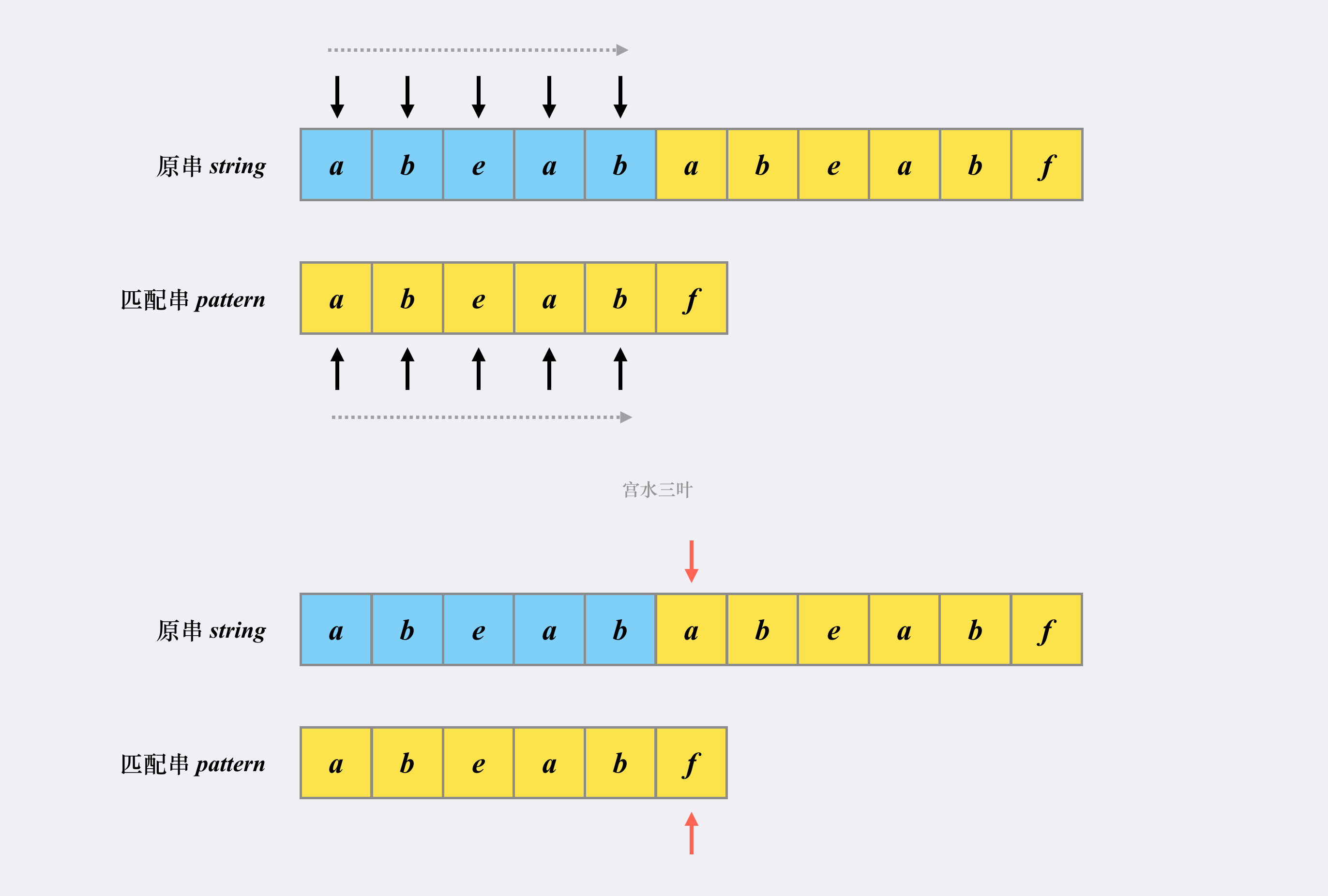
方法2：Knuth-Morris-Pratt 算法（宫水三叶：https://leetcode-cn.com/problems/implement-strstr/solution/shua-chuan-lc-shuang-bai-po-su-jie-fa-km-tb86/）

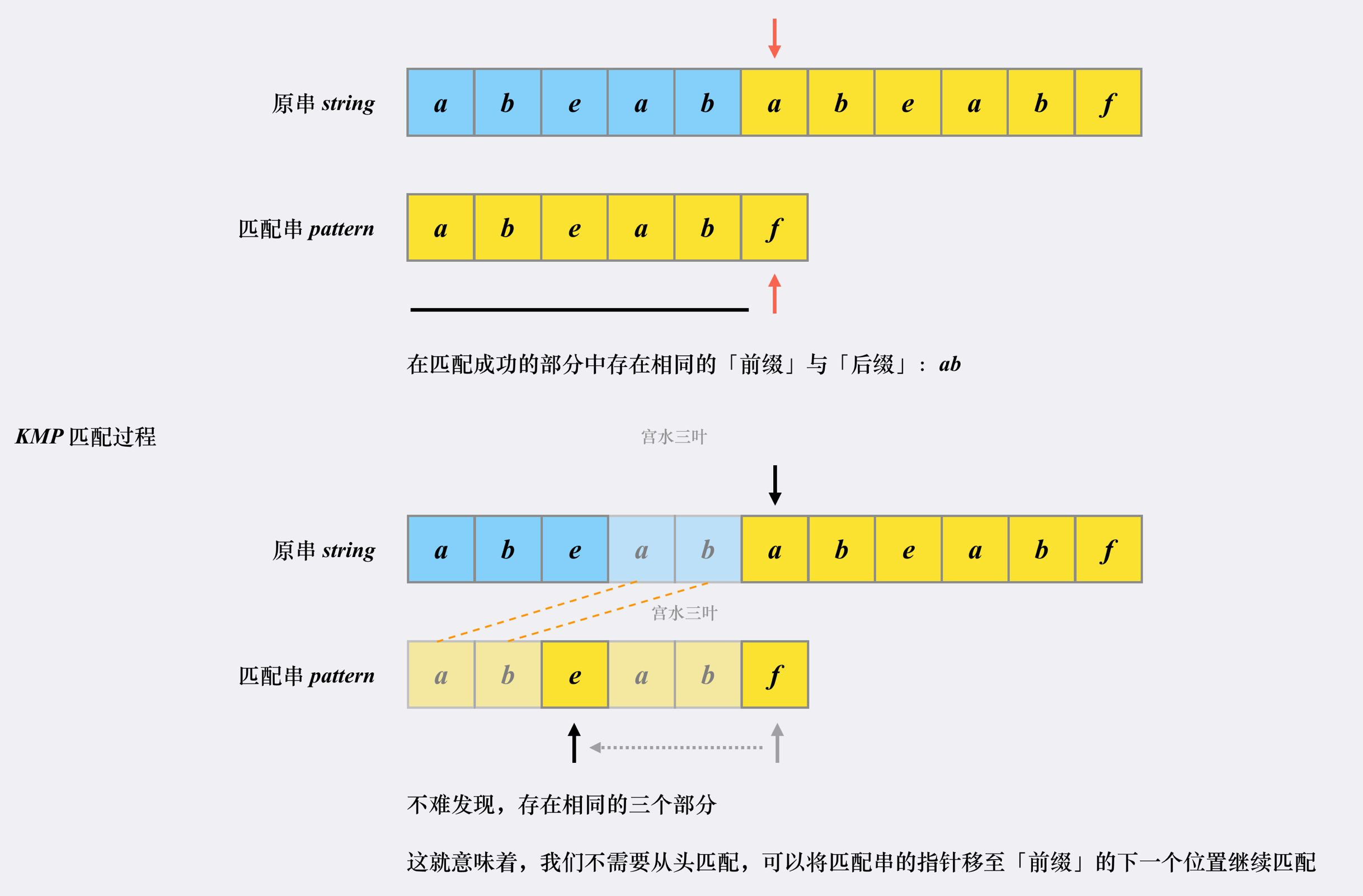
KMP 算法是一个快速查找匹配串的算法，它的作用其实就是本题问题：如何快速在「原字符串」中找到「匹配字符串」。

KMP 之所以能够在O(m+n) 复杂度内完成查找，是因为其能在「非完全匹配」的过程中提取到有效信息进行复用，以减少「重复匹配」的消耗。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

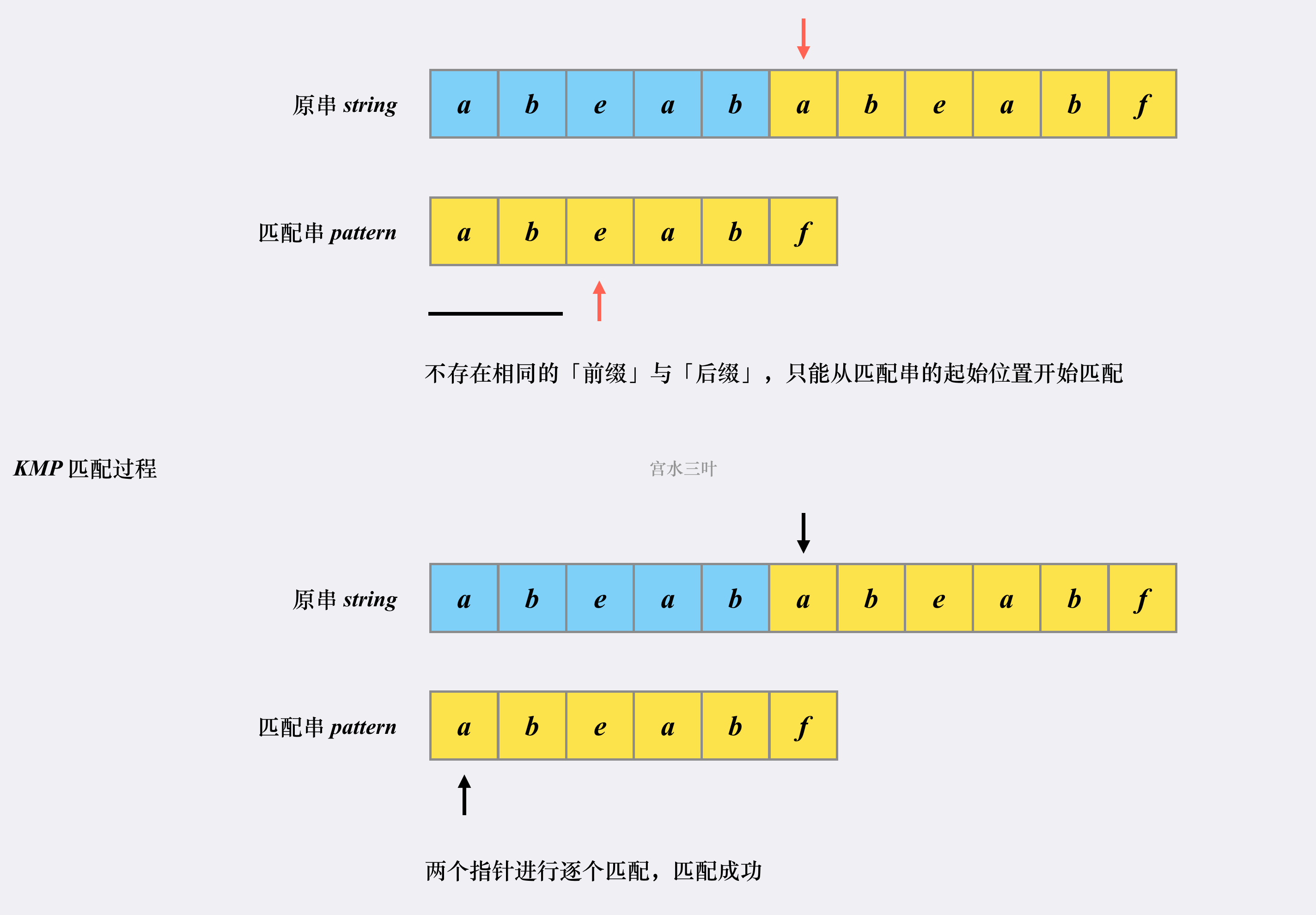
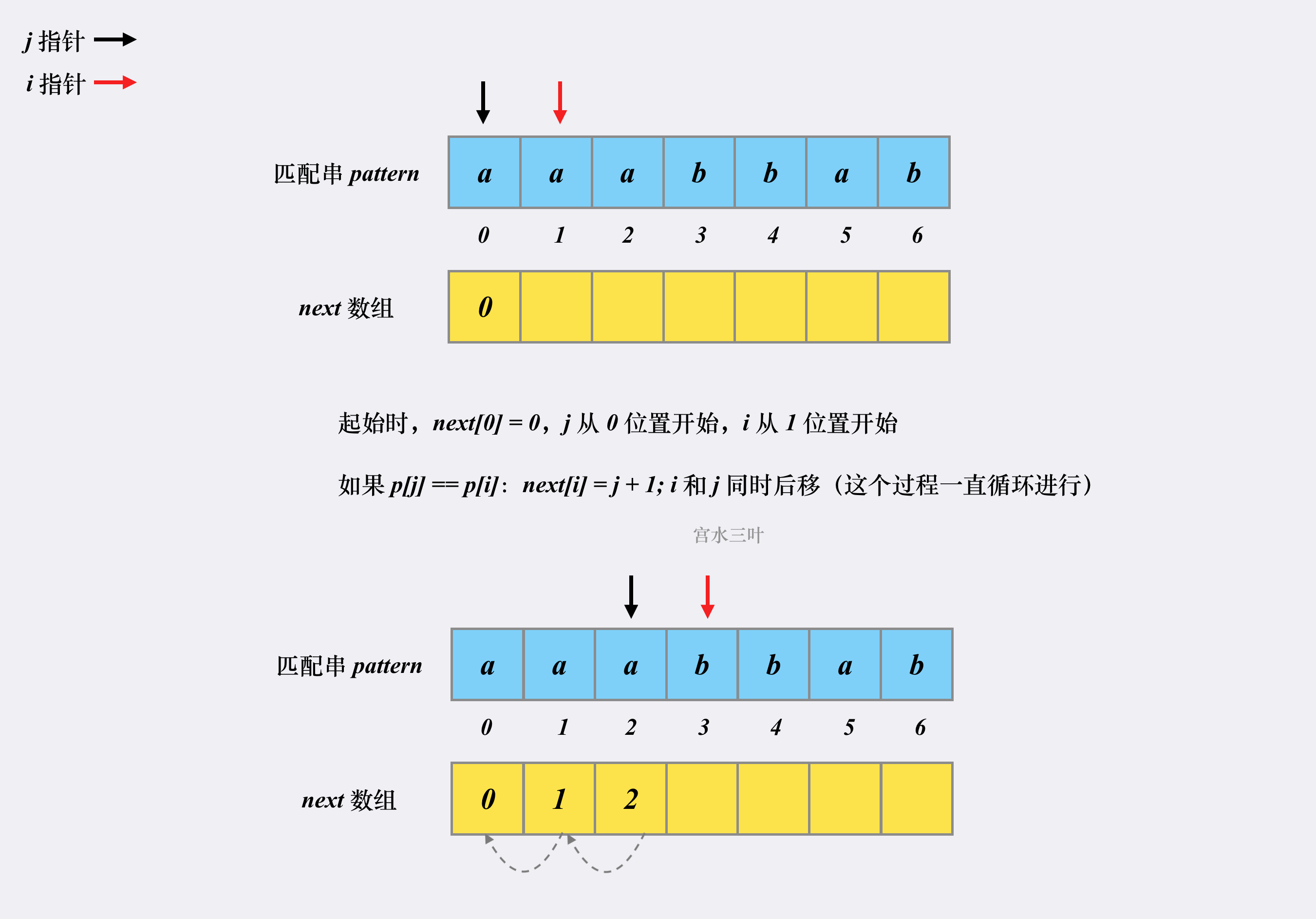
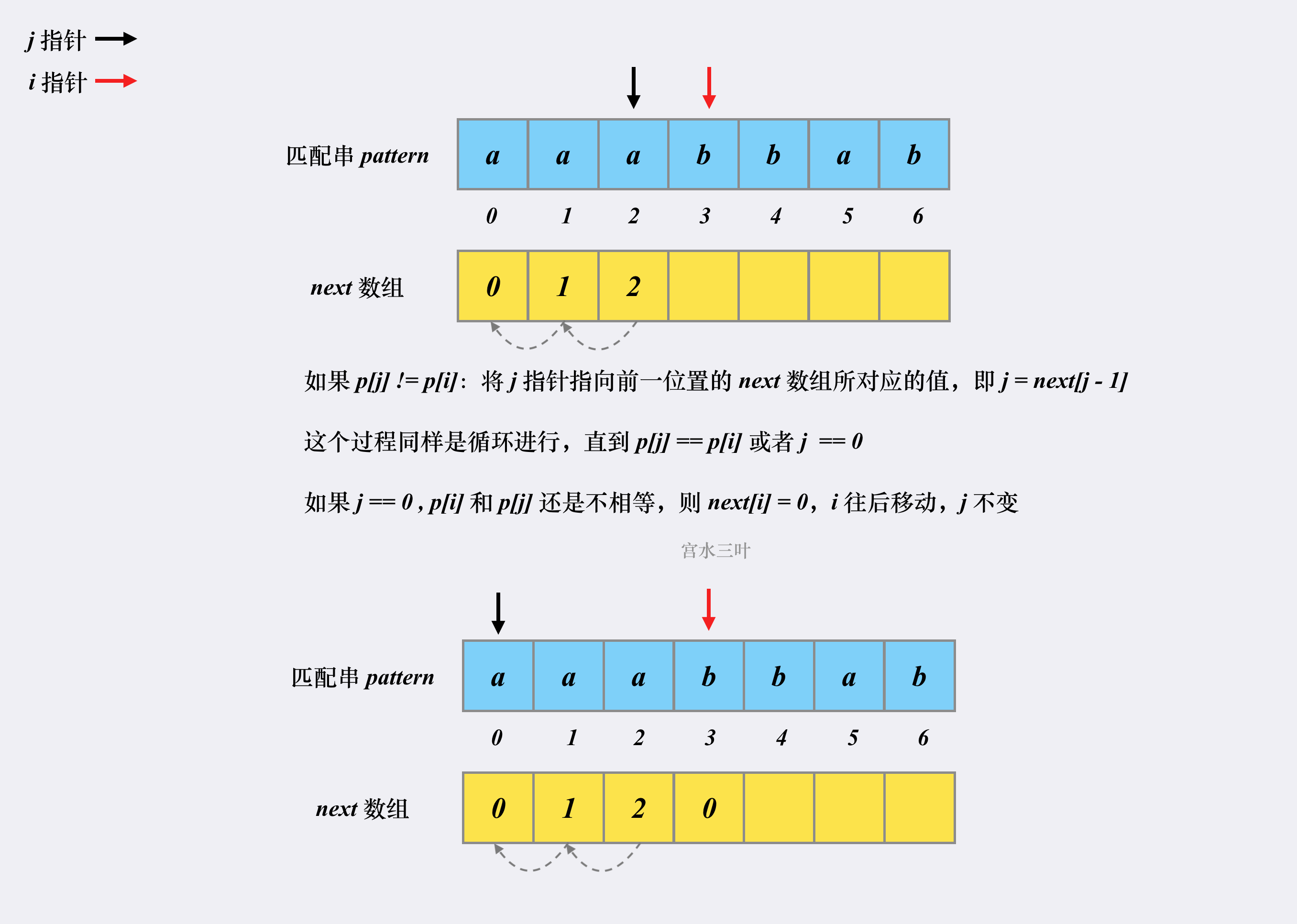
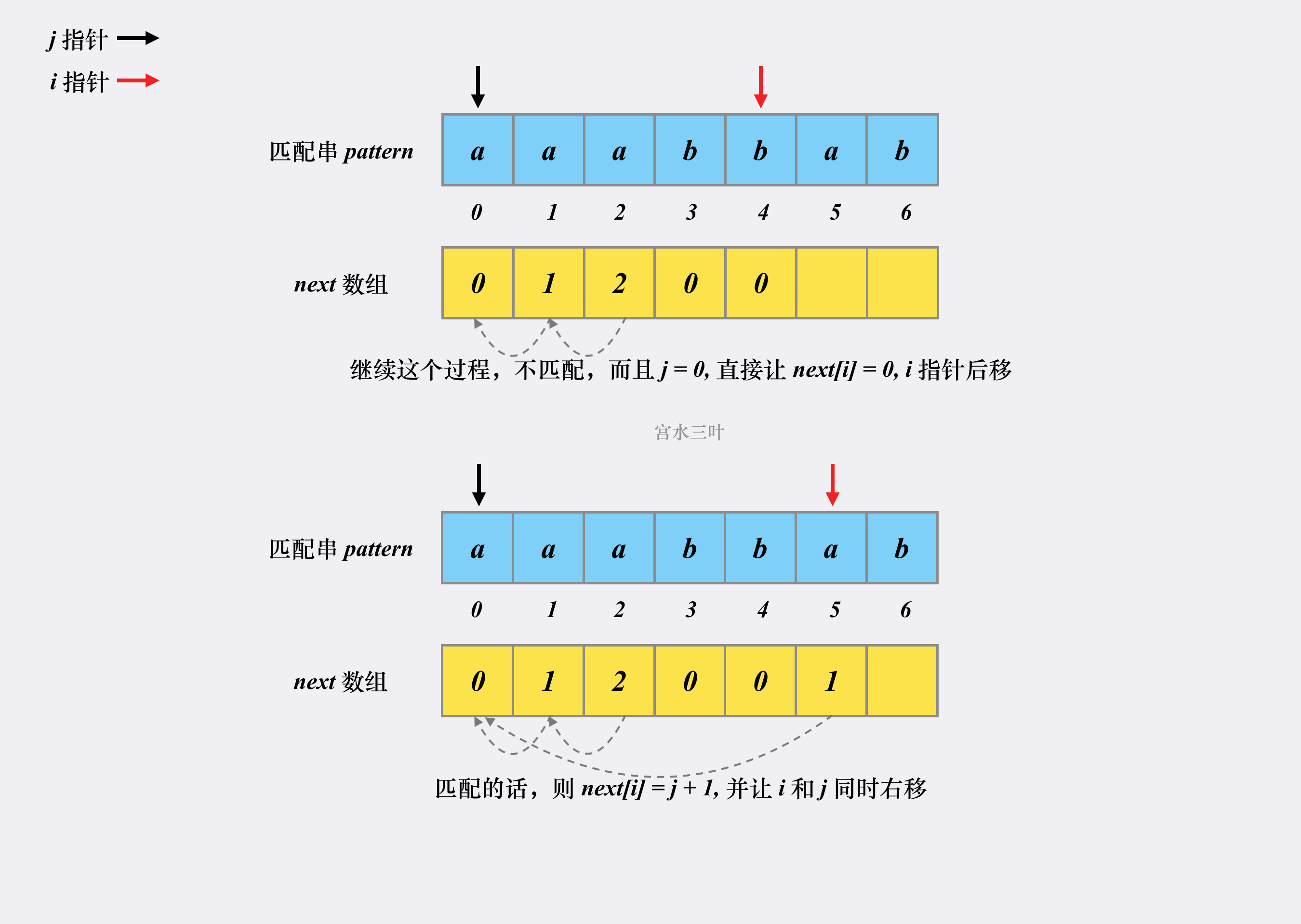
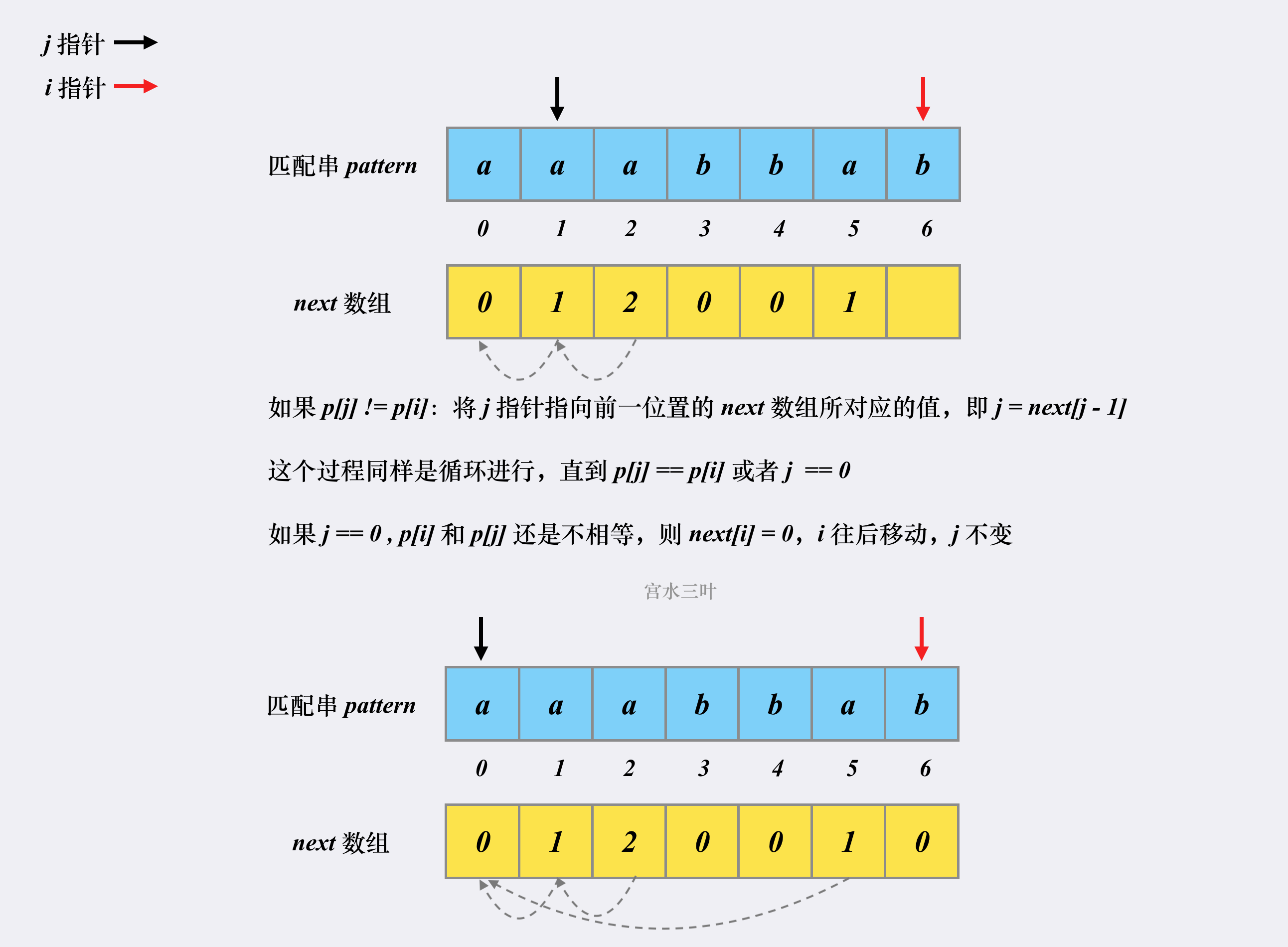
class Solution {
    // KMP 算法
    // ss: 原串(string)  pp: 匹配串(pattern)
    public int strStr(String ss, String pp) {
        if (pp.isEmpty()) return 0;
        
        // 分别读取原串和匹配串的长度
        int n = ss.length(), m = pp.length();
        // 原串和匹配串前面都加空格，使其下标从 1 开始
        ss = " " + ss;
        pp = " " + pp;

        char[] s = ss.toCharArray();
        char[] p = pp.toCharArray();

        // 构建 next 数组，数组长度为匹配串的长度（next 数组是和匹配串相关的）
        int[] next = new int[m + 1];
        // 构造过程 i = 2，j = 0 开始，i 小于等于匹配串长度 【构造 i 从 2 开始】
        for (int i = 2, j = 0; i <= m; i++) {
            // 匹配不成功的话，j = next(j)
            while (j > 0 && p[i] != p[j + 1]) j = next[j];
            // 匹配成功的话，先让 j++
            if (p[i] == p[j + 1]) j++;
            // 更新 next[i]，结束本次循环，i++
            next[i] = j;
        }

        // 匹配过程，i = 1，j = 0 开始，i 小于等于原串长度 【匹配 i 从 1 开始】
        for (int i = 1, j = 0; i <= n; i++) {
            // 匹配不成功 j = next(j)
            while (j > 0 && s[i] != p[j + 1]) j = next[j];
            // 匹配成功的话，先让 j++，结束本次循环后 i++
            if (s[i] == p[j + 1]) j++;
            // 整一段匹配成功，直接返回下标
            if (j == m) return i - m;
        }

        return -1;
    }
}