Redis Zset类型跳跃表算法实现(JAVA)
Redis 有序集合类型(zset) 底层核心实现的机制就是跳跃表
最近公司搞了技术分享的活动,正好快到我了,最近在研究Redis就说说redis实现的原理吧. 发现还是晚上脑子比较好使,建议看代码时候边看边画图 推荐画图工具 http://draw.io/
首先定义一个双向链表的类
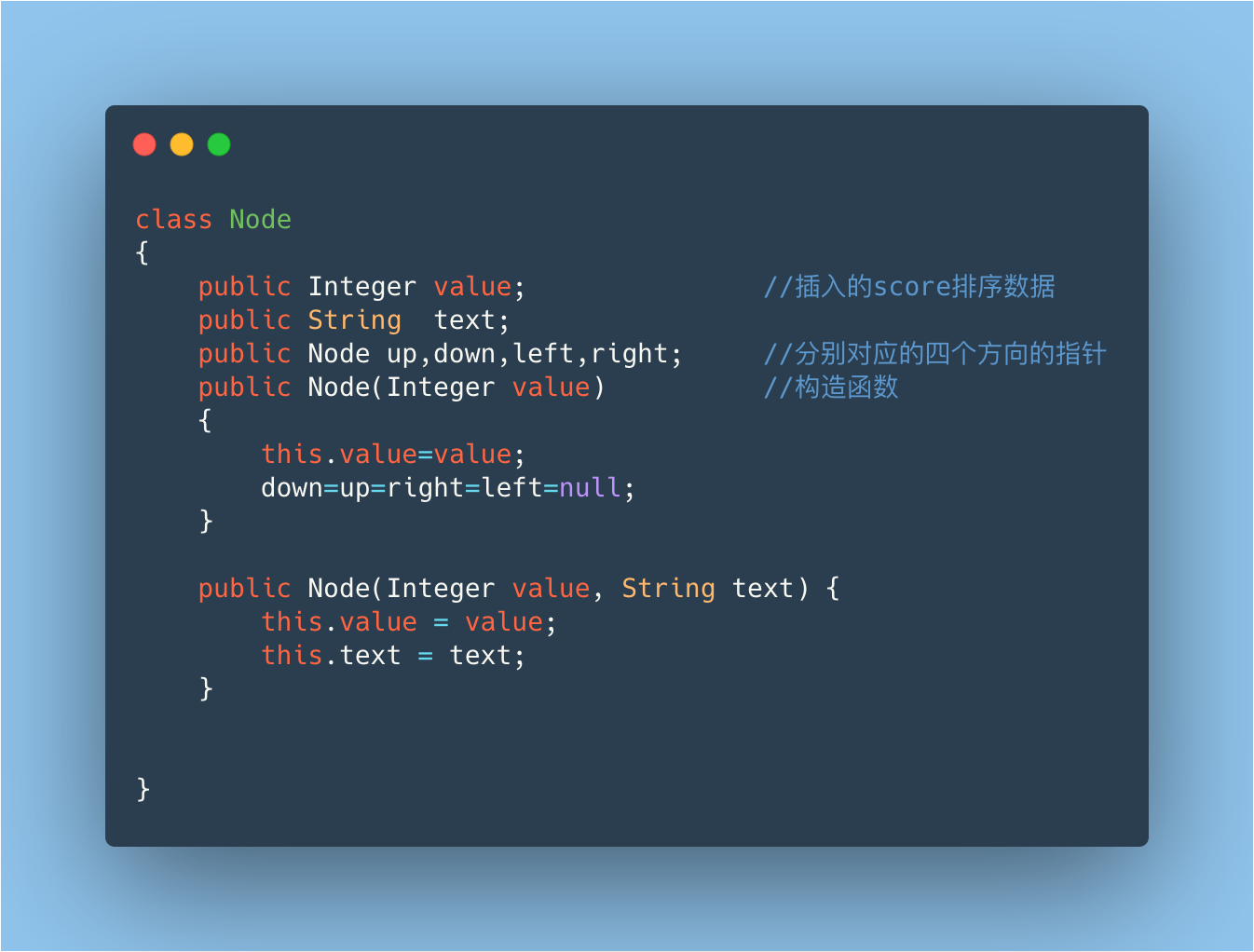
双向链表的流程图
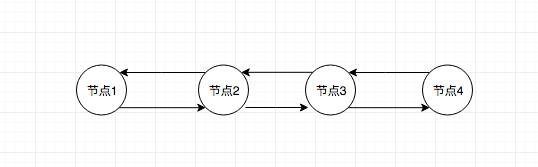
跳跃表的结构图
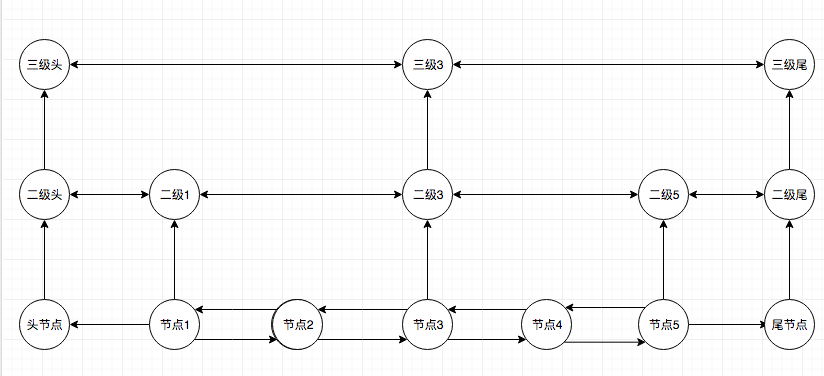

跳跃表查找的过程
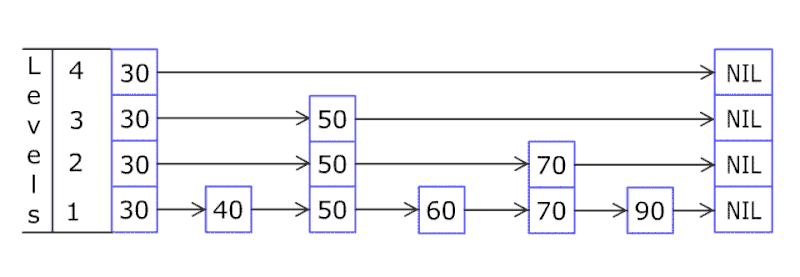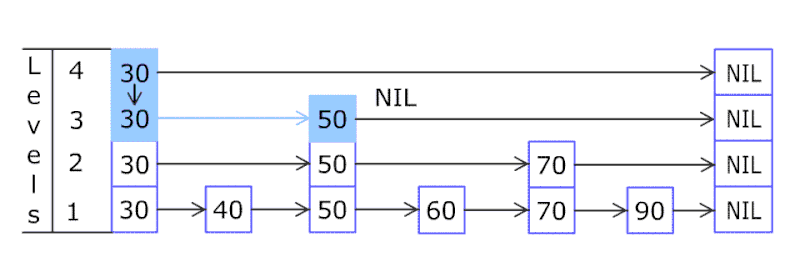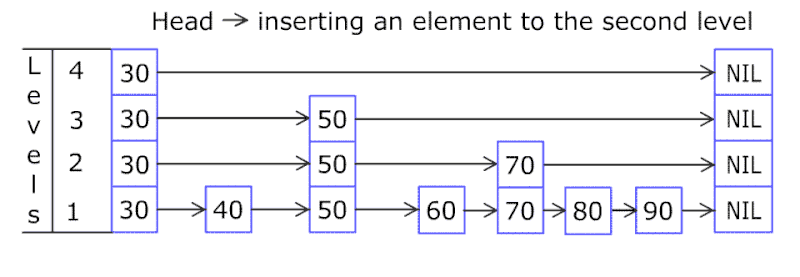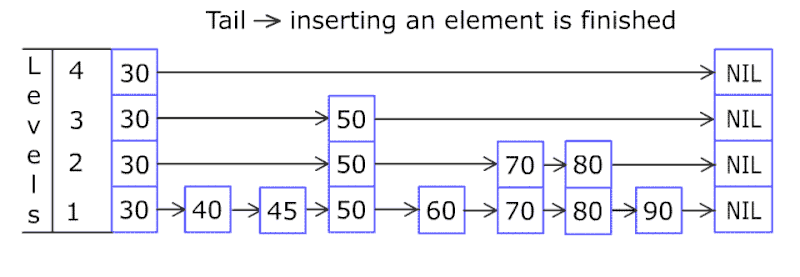
跳跃表结构

具体代码
import wl.redis.Message; import java.util.*; class Node { public Integer value; //插入的score排序数据 public String text; public Node up,down,left,right; //分别对应的四个方向的指针 public Node(Integer value) //构造函数 { this.value=value; down=up=right=left=null; } public Node(Integer value, String text) { this.value = value; this.text = text; } } public class SkipList { private Node head; //最上面一侧的头结点,这里使用的是双链表 private Node tail; //最上面一层的尾节点,这里的头尾节点是不存储数据的,数据域全是null private int level; //表中的最高的层数,就是总共的层数 private int size; //插入节点的个数,头尾节点除外 private Random random; //用来判断是否需要增加高度的随机函数 public SkipList() { level = 0; //level默认是0层,就是只有最下面的一层 head = new Node(null); tail = new Node(null); head.right = tail; //这里初始化成一个只有一层的双链表 tail.left = head; size = 0; //size初始化为0 random = new Random(); } //这个函数的作用是找到插入节点的前面一个节点,这里默认的是将表升序存储 public Node findFirst(Integer value) { Node p = head; while (true) { //判断要插入的位置,当没有查到尾节点并且要插入的数据还是比前面的大的话,就将节点右移,知道找到合适的位置 //这里需要注意的是这里的head代表不一定是最底层的,因此这里的查找都是从最高层进行查找的,如果满足条件就要向下移动 //直到最底层 while (p.right.value != null && p.right.value <= value) { p = p.right; } //向下移动,直到到达最后一层 if (p.down != null) { p = p.down; } else { //到达最底层跳出即可 break; } } return p; //此时这里的p就是要插入节点的前面一个节点 } //这是插入函数,这里先执行插入,然后判断是否需要增加高度 public void insert(int value,String text) { Node curr = findFirst(value); //先找到插入位置的前面一个节点 Node q = new Node(value,text); //新建一个插入的节点 //redis 中不允许score相同和值也相同的出现 if (curr.value!=null && curr.value == q.value && curr.text!=null && String.valueOf(curr.text).equals(String.valueOf(q.text))){ System.out.println("插入的值已经存在"); return; } //下面执行插入步骤,这个和双链表是一样的步骤 q.right = curr.right; q.left = curr; curr.right.left = q; curr.right = q; int i = 0; //表示当前节点所在的层数,开始插入的是在下面插入的,所以开始的时候是在0层 //这里判断是否需要增加高度,每一层相对域下面来说都有二分之一的概率,也就是说每一层增加的概率是(1/2)^n //通俗的说就是每一层的节点是将会保证是下面一层的1/2 while (random.nextDouble() < 0.5) { if (i >= level) { //如果当前插入的节点所处的层数大于等于最大的层数,那么就需要增加高度了,因为这里要保证头尾节点的高度是最高的 //下面的代码就是在头尾节点的上插入新的节点,以此来增加高度 Node p1 = new Node(null); Node p2 = new Node(null); p1.right = p2; p1.down = head; p2.left = p1; p2.down = tail; head.up = p1; //将头尾节点上移,成为最顶层的节点,这就是为什么每次插入和查询的时候都是最上面开始查询的,因为这里的head默认的就是从最上面开始的 tail.up = p2; head = p1; tail = p2; level++; //最高层数加一 } while (curr.up == null) { //当然增加高度就是在插入节点上面新插入一个节点,然后将之与插入的节点相连 //既然这里新插入节点增高了,那么就需要找到与新插入节点上面的那个节点相连接,这里我们将新插入节点的前面的同等高度的节点与之相连 curr = curr.left; } curr = curr.up; //通过前面的一个节点找到与之相连的节点 //下面就是创建一个节点插入到插入节点的头上以此来增加高度,并且这个节点与前面一样高的节点相连 Node e = new Node(value); e.left = curr; //设置的顺序按照新节点先设置,老节点后设置的顺序来 e.right = curr.right; curr.right.left = e; //此时的curr就是与之同等高度的节点 curr.right = e; e.down = q; q.up = e; q = e; //将新插入的节点上移到最上面,因为后面可能还要在这里增加高度,就是在最上面插入新的一模一样的节点 i++; //增加当前所处的高度,这里一定能要记得写上,如果还要继续增加的话,需要判读是否需要增加头尾节的高度 } size++; //节点加一 } //下面是打印每一层节点的情况 //head 最后都会停留在最高一层,一层一层往下跳 public void display() { while (level >= 0) { Node p = head; while (p != null) { System.out.print(p.value + "-------->"); p = p.right; } System.out.println(); System.out.println("*****************************"); level--; //开始跳 head = head.down; //head 指向下层的链表 } } /*在链表中查找某个值是否存在,如果存在找到的节点,当然先从最高层开始查找,如果找到了在比这个值小的最后一个值,那么就顺着这个值的下面开始寻找,按照上面的步骤 再次寻找,如过这个值正好等于要找的值,就返回true,形象的来说就是形成一个梯度的感觉。注意这里返回的节点一定是最底层的节点,利于下面的删除操作 * */ public Node search(int value) { Node p = head; while (true) { /*这里一定要写成p.right.value!=null,如果写成p.right!=null运行可能有错误, 因为这里的尾节点的值为null,但是它的节点不是空的,如果成这样的话,那么节点可能会找到尾节点都没有找到,此时在判断value的值就出现错误 相当与判断tail.right.value<=value,这个肯定是不行的,因为这个节点不存在,是空的更别说值了 */ //从最高层开始判断找到比这个小的最后一个值,就是找到一个节点的前面比value小的,后面的节点的值比value大的 while (p.right.value != null && p.right.value <= value) { p = p.right; //如果没有找到就后移直到找到这个节点 } //如果找到的这个节点不是最底层的话,就向下移动一层,然后循环再次寻找,总之就是从最高层开始,一层一层的寻找 if (p.down != null) { //这个表示上面的循环没有找到的相等的,那么就向下移动一层,而且不管是在最高层就搜到了这个,我还是要跳到最底层 p = p.down; } else { //如果到了最底层了,这里的值仍然没有找到这个值,那么就表示不存在这个值 if (p.value == value) { //判断是否存在value相等的值 return p; //返回节点 } return null; //仍然没有找到返回null } } } //打印最底层的元素 public void dumpAll(){ Node newNode= head; while (newNode.down!=null){ //跳到最底层去 newNode=newNode.down; //指针偏移 } while (newNode.right.value!=null){ System.out.println(newNode.right.value+" ---> "+newNode.right.text); newNode=newNode.right; //指针偏移 } } //打印最底层的元素 public void dumpAllDesc(){ Node newNode= tail; while (newNode.down!=null){ //跳到最底层去 newNode=newNode.down; //指针偏移 } while (newNode.left.value!=null){ System.out.println(newNode.left.value+" ---> "+newNode.left.text); newNode=newNode.left; //指针偏移 } } /* 这里是利用上面的查找函数,找到当前需要删除的节点,当然这个节点是最底层的节点,然后循环从最底层开始删除所有的节点 * */ public void delete(int value) { Node temp = search(value); //这里返回的必须是最底层的节点,因为要从最下面的往上面全部删除所有层的节点,否则的话可能在某一层上仍然存在这个节点 while (temp != null) { temp.left.right = temp.right; temp.right.left = temp.left; temp = temp.up; //节点上移,继续删除上一层的节点 } } public static void main(String args[]) { SkipList skipList = new SkipList(); Random random = new Random(); skipList.insert(33,"小明"); skipList.insert(33,"小明"); skipList.insert(44,"小亮"); skipList.insert(44,"小亮"); skipList.insert(11,"小贾"); for (int i = 0; i < 500; i++) { int value = (int) (random.nextDouble() * 1000); skipList.insert(value, UUID.randomUUID().toString()); System.out.println(value); } Node p = skipList.search(22); // skipList.delete(44); if (p != null) { System.out.println(p.value); } else System.out.println("没有找到"); skipList.display(); } }
~~~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号