gaussian算子

https://www.cnblogs.com/wangguchangqing/p/6407717.html

https://blog.csdn.net/godadream/article/details/81568844

　　数值图像处理中，高斯滤波主要可以使用两种方法实现。一种是离散化窗口滑窗卷积，另一种方法是通过傅里叶变化。最常见的就是滑窗实现，只有当离散化的窗口非常大，用滑窗计算量非常大的情况下，可能会考虑基于傅里叶变化的实现方法。所以本文将主要介绍滑窗实现的卷积。

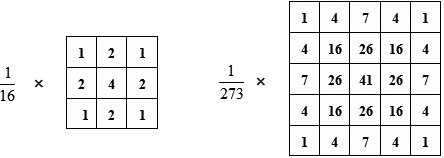
　　离散化窗口划船卷积时主要利用的是高斯核，高斯核的大小为奇数，因为高斯卷积会在其覆盖区域的中心输出结果。常用的高斯模板有如下几种形式：

1、二维高斯函数

　　

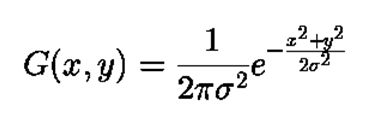
2、取样模板

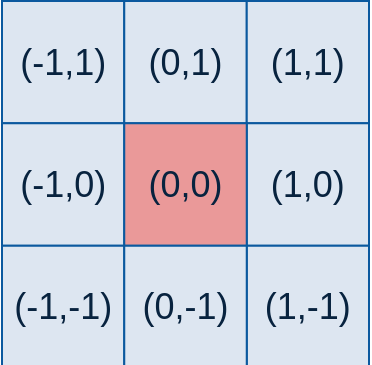
3、获取模板

　　将模板各个位置坐标代入高斯函数G中，就得到该位置的模板值；并将9个位置的值求和sum，理想情况sum=1，这里会将各个模板值除以sum；

4、模板形式

（1）小数模板：直接由高斯函数和位置模板计算得到；(高斯核为3X3，sigma=0.8)

0.057118	0.12476	0.057118
0.12476	0.2725	0.12476
0.057118	0.12476	0.057118

（2）整数模板：对小数模板获得的模板进行归一化处理，即将小数模板的每个值除以模板左上角的值；(高斯核为3X3，sigma=0.8)

1	2.1842	1
2.1842	4.7707	2.1842
1	2.1842	1

　　经过四舍五入和添加系数为：