排序算法

https://www.cnblogs.com/zhaoshuai1215/p/3448154.html

1、插入排序

      遍历数组，遍历到i时，a₀,a₁...a_i-1是已经排好序的，取出a_i，从a_i-1开始向前和每个比较大小；如果ai小于ai-1，则将a_i-1移动到a_i位置（从小到大排序），继续将a_i与前面的比较，如果a_i还是小于前面a_x，则将a_x元素向后移动；如果不小于，则放到正在比较的元素之后，此位置的元素已经移动到后面去了。可见相等元素比较是，原来靠后的还是拍在后边，所以插入排序是稳定的。

      当待排序的数据基本有序时，插入排序的效率比较高，只需要进行很少的数据移动。

void insertion_sort(int a[], int n){
int i, j, v;
for (i = 1; i < n; i++){
for (v = a[i], j = i - 1; j >= 0&&v<a[j]; j--){
a[j+1]=a[j];
}
a[j+1] = v;
}
}

 2、冒泡排序

      冒泡排序

      冒泡排序的名字很形象，实际实现是相邻两节点进行比较，大的向后移一个，经过第一轮两两比较和移动，最大的元素移动到了最后，第二轮次大的位于倒数第二个，依次进行。这是最基本的冒泡排序，还可以进行一些优化。

      优化一：如果某一轮两两比较中没有任何元素交换，这说明已经都排好序了，算法结束，可以使用一个Flag做标记，默认为false，如果发生交互则置为true，每轮结束时检测Flag，如果为true则继续，如果为false则返回。

      优化二：某一轮结束位置为j，但是这一轮的最后一次交换发生在lastSwap的位置，则lastSwap到j之间是排好序的，下一轮的结束点就不必是j--了，而直接到lastSwap即可，代码如下：

void bubble_sort(int a[], int n){
    int i, j, lastswap, tmp;
    for (j = n-1; j>0; j=lastswap){
        lastswap = 0;
        for (i = 0; i < j; i++){
            if (a[i]>a[i + 1]){
                tmp = a[i];
                a[i] = a[i + 1];
                a[i + 1] = tmp;
                lastswap = i;
            }
        }
    }
}

 3、希尔排序

 希尔排序是对插入排序的优化，基于以下两个认识：1. 数据量较小时插入排序速度较快，因为n和n²差距很小；2. 数据基本有序时插入排序效率很高，因为比较和移动的数据量少。

      因此，希尔排序的基本思想是将需要排序的序列划分成为若干个较小的子序列，对子序列进行插入排序，通过则插入排序能够使得原来序列成为基本有序。这样通过对较小的序列进行插入排序，然后对基本有序的数列进行插入排序，能够提高插入排序算法的效率。

      希尔排序的划分子序列不是像归并排序那种的二分，而是采用的叫做增量的技术，例如有十个元素的数组进行希尔排序，首先选择增量为10/2=5，此时第1个元素和第（1+5）个元素配对成子序列使用插入排序进行排序，第2和（2+5）个元素组成子序列，完成后增量继续减半为2，此时第1个元素、第（1+2）、第（1+4）、第（1+6）、第（1+8）个元素组成子序列进行插入排序。这种增量选择方法的好处是可以使数组整体均匀有序，尽可能的减少比较和移动的次数，二分法中即使前一半数据有序，后一半中如果有比较小的数据，还是会造成大量的比较和移动，因此这种增量的方法和插入排序的配合更佳。

      希尔排序的时间复杂度和增量的选择策略有关，上述增量方法造成希尔排序的不稳定性。

 

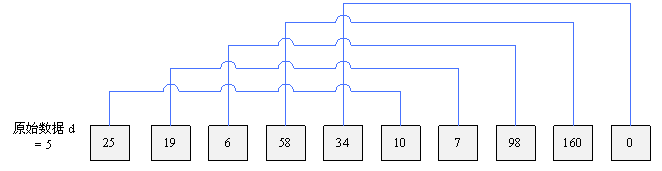
void shell_sort(int a[], int n){
    int d, i, j, tmp;
    for (d = n / 2; d >= 1; d = d / 2){
        for (i = d; i < n; i++){
            tmp = a[i];
            for (j = i - d; j >= 0 && a[j]>tmp; j = j - d)
                a[j + d] = a[j];
            a[j + d] = tmp;

        }
    }
}