字典树（前缀树）（转）

原文地址：https://zhuanlan.zhihu.com/p/28891541

下面介绍前缀树

Trie树，即字典树，又称单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：最大限度地减少无谓的字符串比较。

Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

前缀树的3个基本性质：

根节点不包含字符，除根节点外每一个节点都只包含一个字符。
从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
每个节点的所有子节点包含的字符都不相同。

前缀树查询和哈希查询的比较（示相对情况而定）：

通常字典树的查询时间复杂度是O(logL)，L是字符串的长度。所以效率还是比较高的。

网上的一部分文章说的都是字典树的效率比hash表高。我觉得还是相对来看比较好，各有个的特点吧。

hash表，通过hash函数把所有的单词分别hash成key值，查询的时候直接通过hash函数即可，都知道hash表的效率是非常高的为O(1)，直接说字典树的查询效率比hash高，难道有比O(1)还快的- -。

hash：

当然对于单词查询，如果我们hash函数选取的好，计算量少，且冲突少，那单词查询速度肯定是非常快的。那如果hash函数的计算量相对大呢，且冲突律高呢？

这些都是要考虑的因素。且hash表不支持动态查询，什么叫动态查询，当我们要查询单词apple时，hash表必须等待用户把单词apple输入完毕才能hash查询。

当你输入到appl时肯定不可能hash吧。

字典树（tries树）：

对于单词查询这种，还是用字典树比较好，但也是有前提的，空间大小允许，字典树的空间相比较hash还是比较浪费的，毕竟hash可以用bit数组。

那么在空间要求不那么严格的情况下，字典树的效率不一定比hash若，它支持动态查询，比如apple，当用户输入到appl时，字典树此刻的查询位置可以就到达l这个位置，那么我在输入e时光查询e就可以了（更何况如果我们直接用字母的ASCII作下标肯定会更快）！字典树它并不用等待你完全输入完毕后才查询。

所以效率来讲我认为是相对的。

---------------------------------------------------------------------------------------------------------------------------

接下来通过案例来介绍前缀树的具体操作。

题目：给你100000个长度不超过10的单词。对于每一个单词，我们要判断他出没出现过，如果出现了，求第一次出现在第几个位置。

如果我们使用一般的方法，没查询一个单词都去遍历一遍，那么时间复杂度将为O(n^2),这对于100000这么大的数据是不能够接受的。假如我们要查找单词student。那我们通过前缀树只需要查找s开头的即可，然后接下来查询t开头的即可，对于大量的数据可以省去不小的时间。

树结构：

其中count表示以当前单词结尾的单词数量。

prefix表示以该处节点之前的字符串为前缀的单词数量。

public class TrieNode {
    int count;
    int prefix;
    TrieNode[] nextNode=new TrieNode[26];
    public TrieNode(){
        count=0;
        prefix=0;
    }
}
 

1.前缀树的创建

好比假设有b，abc，abd，bcd，abcd，efg，hii 这6个单词,那我们创建trie树就得到

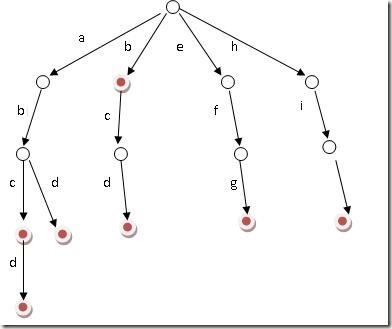
//插入一个新单词
    public static void insert(TrieNode root,String str){
        if(root==null||str.length()==0){
            return;
        }
        char[] c=str.toCharArray();
        for(int i=0;i<str.length();i++){
            //如果该分支不存在，创建一个新节点
            if(root.nextNode[c[i]-'a']==null){
                root.nextNode[c[i]-'a']=new TrieNode();
            }
            root=root.nextNode[c[i]-'a'];
            root.prefix++;//注意，应该加在后面
            }
        
        //以该节点结尾的单词数+1
        root.count++;
    }

2.查询以str开头的单词数量，查询单词str的数量

 //查找该单词是否存在，如果存在返回数量，不存在返回-1
    public static int search(TrieNode root,String str){
        if(root==null||str.length()==0){
            return -1;
        }
        char[] c=str.toCharArray();
        for(int i=0;i<str.length();i++){
            //如果该分支不存在，表名该单词不存在
            if(root.nextNode[c[i]-'a']==null){
                return -1;
            }
            //如果存在，则继续向下遍历
            root=root.nextNode[c[i]-'a'];    
        }
        
        //如果count==0,也说明该单词不存在
        if(root.count==0){
            return -1;
        }
        return root.count;
    }
    
    //查询以str为前缀的单词数量
    public static int searchPrefix(TrieNode root,String str){
        if(root==null||str.length()==0){
            return -1;
        }
        char[] c=str.toCharArray();
        for(int i=0;i<str.length();i++){
            //如果该分支不存在，表名该单词不存在
            if(root.nextNode[c[i]-'a']==null){
                return -1;
            }
            //如果存在，则继续向下遍历
            root=root.nextNode[c[i]-'a'];    
        }
        return root.prefix;
    }

3.在主函数中测试

    public static void main(String[] args){
        TrieNode newNode=new TrieNode();
        insert(newNode,"hello");
        insert(newNode,"hello");
        insert(newNode,"hello");
        insert(newNode,"helloworld");
        System.out.println(search(newNode,"hello"));
        System.out.println(searchPrefix(newNode,"he"));
    }

/**
输出：3   4
**/

posted @ 2020-08-07 16:47 Valentino 阅读(286) 评论(0) 编辑收藏举报

刷新页面返回顶部

Valentino的博客

字典树（前缀树）（转）

公告