ODT 珂朵莉树 详解
人们都说珂教兴国,无奈珂学家里数我最菜,只会背一背ODT板子
珂朵莉镇楼
名字来源
ODT全称Old Driver Tree,中文名 珂朵莉树
有人为了CF896C发明了这个算法,这道题又和珂朵莉有关,所以这个算法叫做珂朵莉树
另外,由于发明者(lxl)的原因,也珂叫ODT(Old Driver Tree).
Warning!
ODT可以解决一些线段树不能解决的问题,如区间次幂求和
但要求数据随机,随机下跑得很快,开了O2更快
数据不随机就是个假算法,开了O2也没用
前置芝士:set
这个大佬讲的很详细
据说set是用红黑树实现的,O2下效率很高
set是自带排序+去重的
set自带一些函数
迭代器类似于指针
begin() 返回set容器的第一个元素
end() 返回set容器的最后一个元素的后一个
clear() 删除set容器中的所有的元素
empty() 判断set容器是否为空
size() 返回当前set容器中的元素个数
lower_bound() 返回指向大于或等于某值的第一个元素的迭代器
upper_bound() 返回大于某个值元素的迭代器
find() 返回一个指向被查找到元素的迭代器,如果没找到则返回end()。
count() 返回查找set中某个某个键值出现的次数,结果只会是0/1
erase(iterator) 删除定位器iterator指向的值
erase(key_value) 删除键值key_value的值
insert(key_value) 将key_value插入到set中,返回值是 pair< set
最后一个看不懂没关系,只要知道insert().first返回的是一个迭代器就行
另外,set的储存元素是结构体时,需要重载"<"
像这样
friend bool operator <(const node &a,const node &b){return a.l<b.l;} `
下面是我的结构体写法
struct node
{
int l,r;
mutable long long val;
node(int L=0,int R=-1,int V=0):l(L),r(R),val(V){}
friend bool operator <(const node &a,const node &b){return a.l<b.l;}
};
算法流程
想看视频讲解的点这里
ODT主要是依靠set来实现的,用来维护一个序列
set里装的是结构体元素,每个元素有3个基本属性:L,R,val
就相当于把序列分为若干个"块",每一个块里的元素在序列上相连且权值相等
L和R是块的左右端点,val是权值
借大佬的图一用
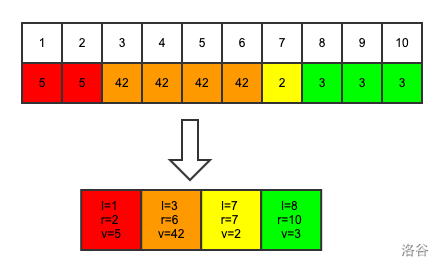
``
关键操作
一般写ODT时都有define IT set
split
将含有pos的区间[l,r]拆分为[l,pos-1)和[pos,r]
同时返回一个指向[pos,r]的迭代器
IT split(int pos)
{
IT it=s.lower_bound(node(pos));
if(it!=s.end()&&it->l==pos)return it;
--it;
int ll=it->l,lr=it->r;
char lv=it->v;
s.erase(it);
s.insert(node(ll,pos-1,lv));
return s.insert(node(pos,lr,lv)).first;
}
Assign/tuiping
极其暴力的一个操作
把原先的删了,再重新加一个新的
注意split时,要先split(r+1),再 split(l),否则会RE,原因有点复杂,想知道的看这个
void tuiping(int l,int r,char v)
{
IT it2=split(r+1),it1=split(l);
s.erase(it1,it2);
s.insert(node(l,r,v));
}
其他操作
以CF896C为例,下面为了美观自动省去了long long和取模操作
这些真的是一个比一个暴力
区间求x次幂和
线段树无法完成此操作
用ODT的话暴力加起来就行
int sum(int l,int r,int x,int mod)
{
IT it2=split(r+1),it1=split(l);
long long res=0;
for(;it1!=it2;++it1)res=res+(it1->r-it1->l+1)*ksm(it1->val,x,mod);
return res;
}
区间加
暴力加就行
void add(int l,int r,int v)
{
IT it2=split(r+1),it1=split(l);
for(;it1!=it2;++it1)it1->val+=v;
}
区间赋值
Assign原封不动
区间k小
暴力取出来排个序就行
int my_rank(int l, int r, int k)
{
vector<pair<int, int> > vp;
IT itr = split(r+1),itl = split(l);
vp.clear();
for (; itl != itr; ++itl)
vp.push_back(pair<int,int>(itl->val, itl->r - itl->l + 1));
sort(vp.begin(), vp.end());
for (vector<pair<int,int> >::iterator it=vp.begin();it!=vp.end();++it)
{
k -= it->second;
if (k <= 0) return it->first;
}
}
然后这道题就解决啦
后记:
1.要想用ODT一定要看看数据是不是随机的,有的时候出题人会给一部分随机数据的部分分
2.写ODT的时候要小心,写错很容易RE
题单:
下面的好多题都卡了ODT(但还有部分分),可以用来练练手
CF896C Willem, Chtholly and Seniorious这个用ODT可以过
CF915E Physical Education Lessons这个用ODT可以过
P2824 [HEOI2016/TJOI2016]排序 题解 这个用ODT也可以过,还挺快(开O2),没有被卡主要还是因为没有人想得到这题还能用ODT...



 浙公网安备 33010602011771号
浙公网安备 33010602011771号