博客作业06--图
1.学习总结
1.1图的思维导图

1.2 图结构学习体会
-
深度遍历算法:好比一棵树,先访问初始顶点的一个孩子,再从该孩子出发去访问它的其中一个孩子,到叶子节点再逐层返回,直至所有孩子都被访问过为止,建议使用递归
-
广度遍历算法:也好比一棵树,访问初始顶点的所有没有被访问过的孩子,再从访问的孩子里访问它的所有没有被访问过的孩子,直至所有孩子都被访问过为止,建议使用队列
-
Prim和Kruscal算法:两者都是求全图最短路径,但是Prim算法是从已有集合顶点中选取最短路径,再将最短路径终点的顶点加入集合,依次重复.Kruscal算法是将权值从小到大排序然后再依次选出
-
Dijkstra算法:找出最便宜的节点,即可在最短时间内前往的节点。对于该节点的所有邻居,检查是否有前往它们的更短路径,如果有,就更新其开销。处理过的节点,进行标记,以后将不再处理。重复以上过程,直到对图中的每个节点都这样做了。计算出最终路径。
-
拓扑排序算法:很简单,其实就是删去找入度为0的顶点,同时将其出度对应的顶点的入度减1,直至不存在入度为0的顶点
2.PTA实验作业
2.11题目1:7-1 图着色问题
2.12 设计思路(伪代码或流程图)
#include <iostream>
#include <cstring>
#include <set>
using namespace std;
int g[501][501]={0};
int color[501] = { 0 };
int search(int v)
{
遍历邻接矩阵
如果两点(i,j)已连接,且颜色相同color[i]==color[j],返回false
否则返回true
}
int main
{
g[501][501]邻接矩阵输入连接图
color[501]输入并保存颜色
col集合判断颜色数量
如果颜色数量正确和search函数返回true,则输出yes
否则输入no
}
2.13 代码截图
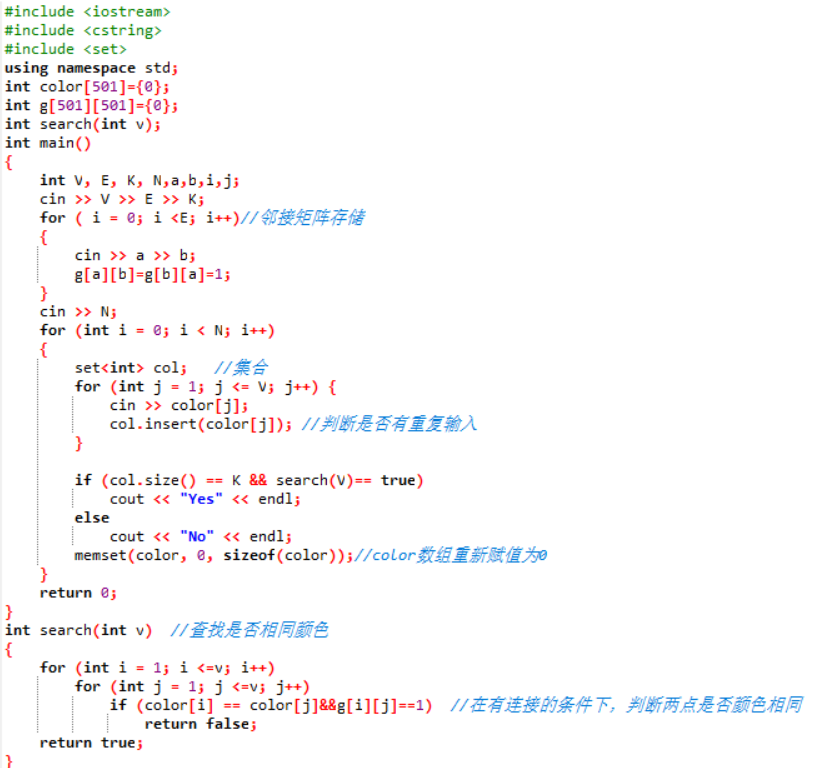
2.14 PTA提交列表说明。

这道题虽然是一遍过,但是是在借鉴别人的代码下才写出来的,有一些自己不是很熟悉的东西,这里要在提及一下,set col创建了一个col集合,是一种包含已排序对象的关联容器,col.insert(color[j])中把元素color[j]存放进col集合中,有重复部分不会再被存储,memset(color, 0, sizeof(color)),将color所指向的某一块内存中的后个sizeof(color)字节的内容全部设置为ch指定的ASCII值,它是对较大的结构体或数组进行清零操作的一种最快方法.
2.21题目2:7-2 排座位
2.22 设计思路(伪代码或流程图)
#include <iostream>
using namespace std;
int g[101][101]={0};
int Find(int a,int b,int v)
{
在已知a,b是敌人的前提下,查找是否有共同朋友
遍历宾客,同一个人对a,b进行判断,如果有共同朋友,返回true
否则,返回false
}
int main
{
输入邻接矩阵,也就是宾客间的关系
循环查询关系:如果宾客间关系为1,说明是朋友,输出No problem
如果宾客间关系为0,说明不是朋友也不是敌人,输出OK
如果宾客间关系为-1且Find函数返回true,说明是敌人但有共同朋友,输出OK but...
以上条件都不满足,说明是敌人并且没有共同朋友 ,输出No way
}
2.23 代码截图

2.14 PTA提交列表说明

这题虽然是一遍过,但是调试过程中也出现些小瑕疵,希望记录在次,当时在写Find函数时,是让i=0开始遍历宾客到v-1结束,如图1,但其实输入的时候并没0这个宾客,而有v这个宾客,测试数据虽然正确,但是如果碰到只有v是共同朋友的数据,那么答案就是错误的,后来改为从i=1到i=v结束,如图2

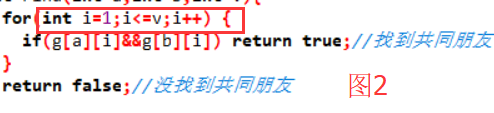
2.31题目3:7-4 公路村村通
2.32 设计思路(伪代码或流程图)
#include<iostream>
#define MAX 1005
#define INF 32767
using namespace std;
void CreateMGraph(int v,int n )
{
邻接矩阵赋初值
如果为对角线上的元素,g[i][j]=0
否则g[i][j]=INF=32767
输入连接图
}
int Prim(int v,int n)
{
prim算法,其中如果当min=INF时输出-1,安全退出函数
否则令 count=count+min
函数最后返回count;
}
int g[1005][1005];
int main()
{
创建邻接矩阵
m=Prim(1,v)从顶点1开始执行prim算法
输出m
}
2.33 代码截图

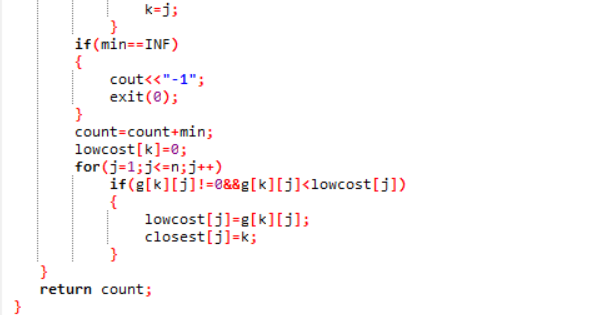
2.34 PTA提交列表说明
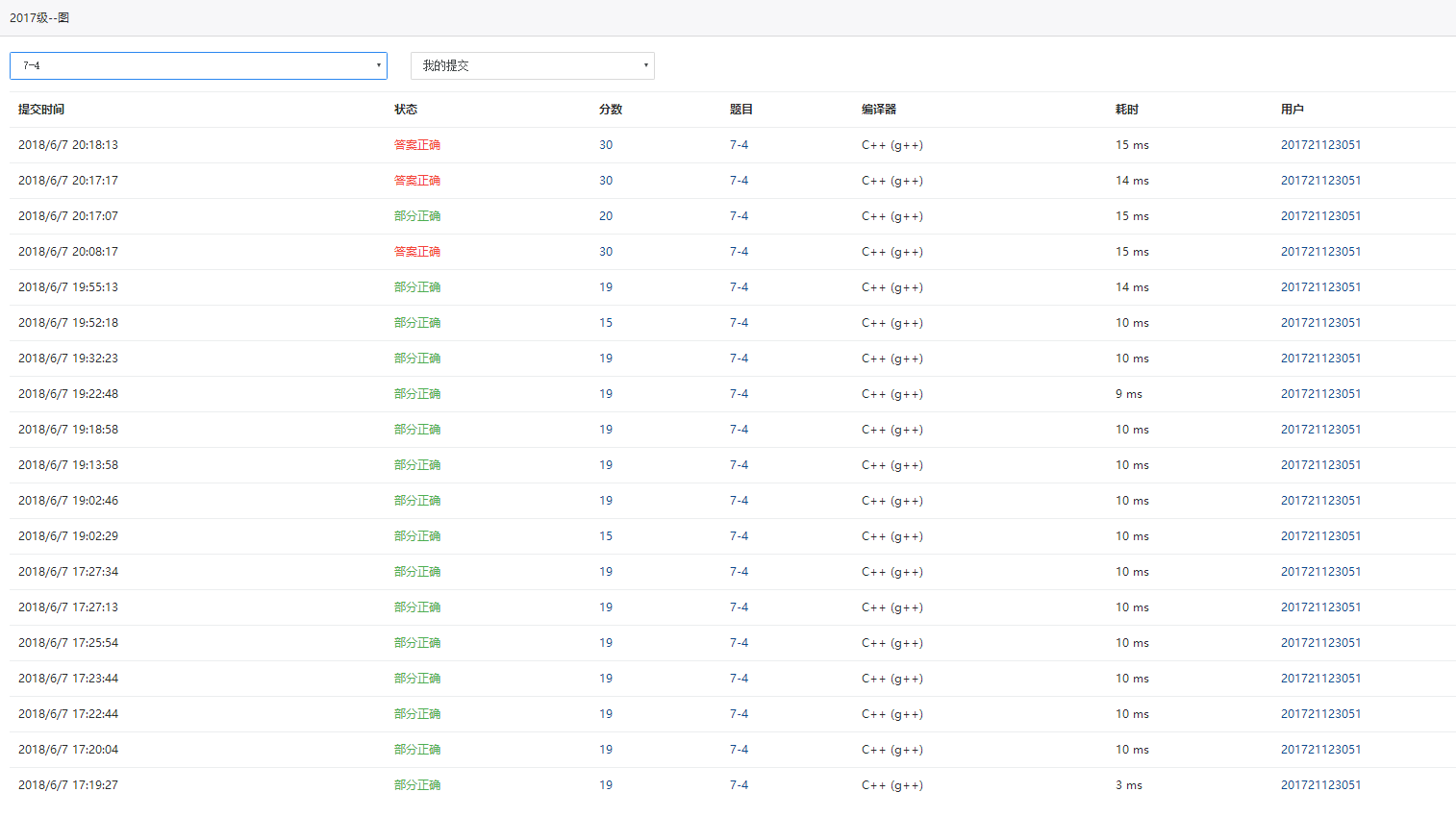
部分正确的原因:答案虽然正确但是老是出现段错误,后来发现同上题一样,遍历邻接矩阵时让i=0开始,导致段错误,改为i=1开始答案正确

这题中输入数据不足以保证畅通,输出−1的情况下,我原本是利用深度遍历,因为如果不畅通说明存在至少存在两个连通图,深度遍历一个顶点,它输不出所有的顶点,而在连通的情况下,随便一个顶点深度遍历都是可以输出全部顶点的,此函数用了20多行的代码,但是经过炳辉同学的指导,他用了3行代码就实现了我20多行代码的功能,确实妙!原因是当不畅通时,miin会等于INF,依据这个特点,在prim算法中加入这个条件,很轻松就能实现,也能说明我对prim算法还是没掌握到.

3.截图本周题目集的PTA最后排名
3.1 PTA排名(截图带自己名字的排名)

3.2 我的总分:250
4. 阅读代码
int Maxdist(ALGraph *G, int v)
{
ArcNode *p;
int Qu[MAXV];//环形队列
int front=0,rear=0;
int visited[MAXV];
int i,j,k;
for(i=0;i<G->n;i++) visited[i]=0;//初始化访问标志数组
rear++Qu[rear]=v;
visited[v]=1;
while(rear!=front)
{ front=(front+1)%MAXV;
k=Qu[front];
p=G->adjlist[k].firstarc;
while(p!=NULL)
{ j=p->adjvex;
if(visited[j]==0)
{ visited[j]==1;
rear=(rear+1)%MAXV;Qu[rear]=j;//进队
}
p=p->nextarc;//找下一个邻接点
}
}
return k;//返回距离v最远的顶点
}



