博客作业04--树

1.学习总结

1.1树结构思维导图

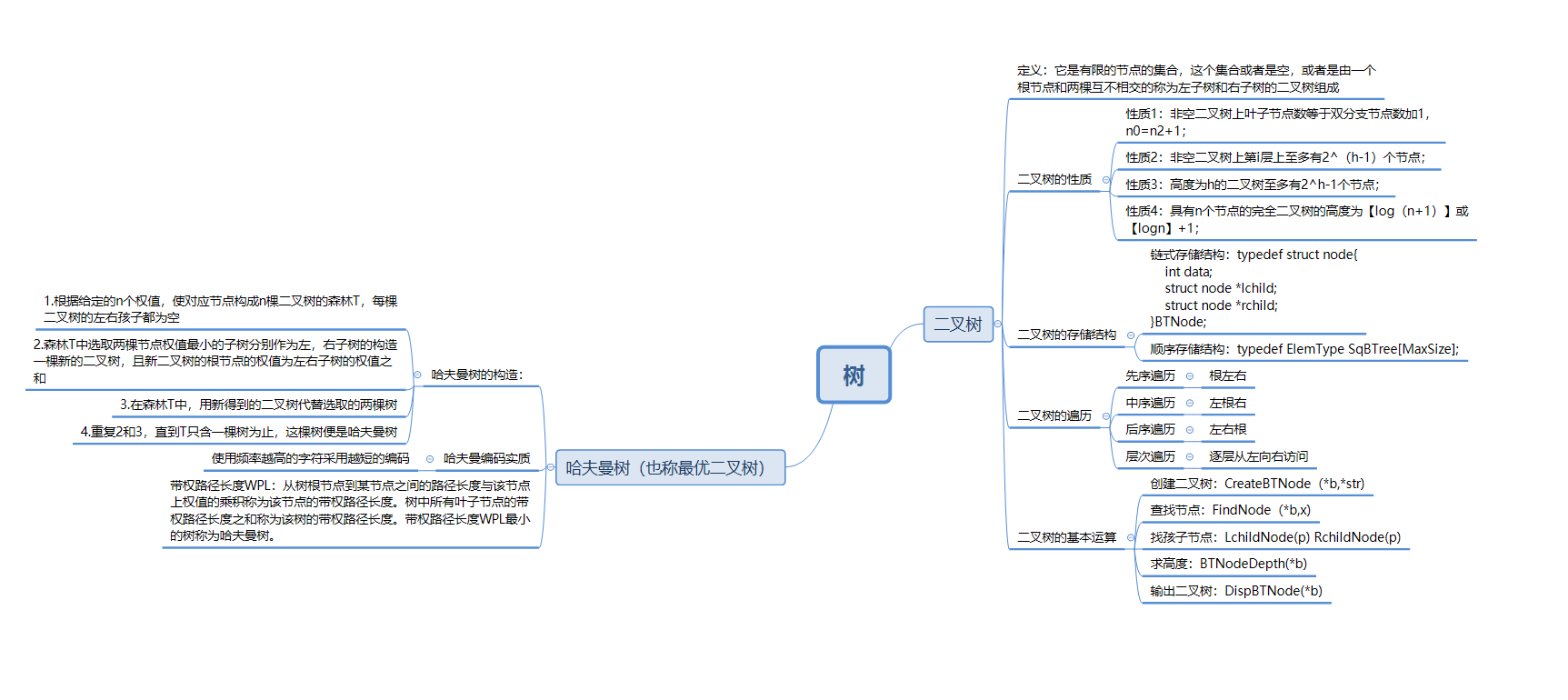
1.2 树结构学习体会

学习树最痛苦的事情就是递归，最开始的先序,中序，后序的递归算法，看了好久才能大致的明白程序的思路，还有就是表达式树的建立，跟栈的中缀转后缀表达式有点类似，但是一用到递归就没那么好理解了，其实重点还是要多花时间去研究书上的代码，学习树的知识，如果对书本的内容不是很熟悉，很难对树有很好的理解，做起题目来也是非常累人的，因为根本不明白程序下一步要怎么走。

2.PTA实验作业

2.11题目： jmu-ds-表达式树

2.12设计思路（伪代码或流程图）

void InitExpTree(BTree &T,string str)
建op栈，op.push('#')
初始化根节点栈：stacktree栈
while(表达式未结束)
{
    if(str[i]==数字字符) 生成一个只有根节点的子树T。stacktree.push(T)
    if(str[i]==运算符) 
    {
        while(str[i]<op栈顶运算符)栈顶优先级别高
        {    创建一个树结点T，数据为op.top()
             stacktree弹出2个根节点T1,T2
             T->lchild=T1;T->rchild=T2;
             stacktree.push(T);
        }
    if(str[i]>op栈顶元素运算符) op.push(str[i])
    if(str[i]==op栈顶运算符) op.pop().
}
double EvaluateExTree(BTree T)
{
         if(T==NULL) return 0;
         if(T->data为数字字符) return T->data-'0'
        else{
                    switch(T->data){
                                             +：return EvaluateExTree(T->lchild) + EvaluateExTree(T->rchild); break；//递归结束标志
                                             -：return EvaluateExTree(T->lchild) - EvaluateExTree(T->rchild); break;  //递归结束标志
                                             *：return EvaluateExTree(T->lchild) * EvaluateExTree(T->rchild); break;  //递归结束标志
                                             /：if((EvaluateExTree(T->rchild)==0)) 输出divide 0 error  exit(0) break;
                                                  else return EvaluateExTree(T->lchild) / EvaluateExTree(T->rchild); break;  //递归结束标志
}

2.13代码截图

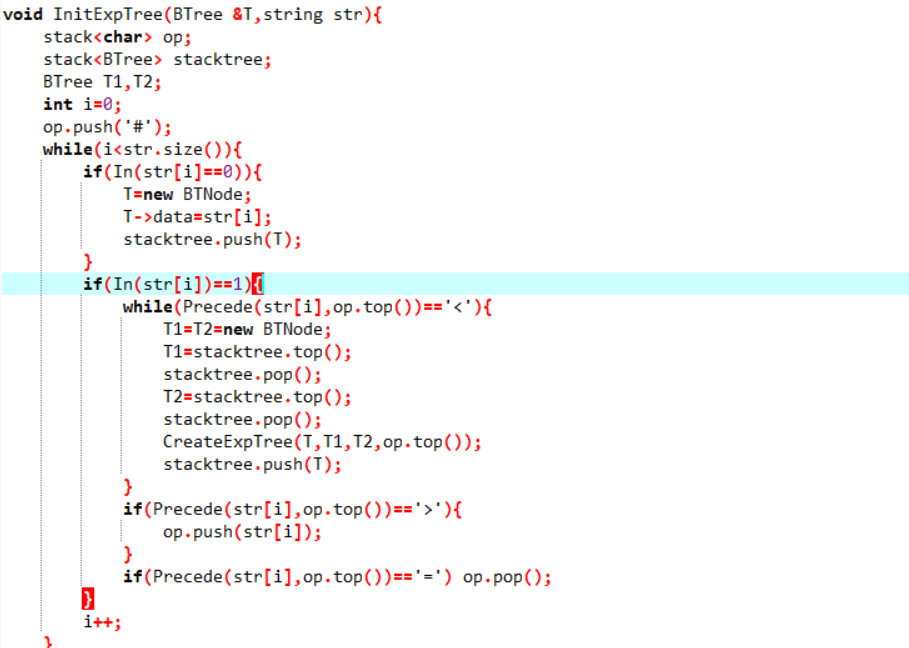
2.14PTA提交列表说明

分析：表达式树的建立是错误的但是思路应该没有问题，但是还是不够完整，在借用志坚同学的表达式树建立代码后调试求值函数，发现除数为0是会多输出一个0，需要使用exit(0)正常退出，不然求值函数会返回0

2.21题目 ：还原二叉树

2.22 设计思路（伪代码或流程图）

BTNode*CreateBT(char *pre,char *in,int n)//根据先序和中序建立二叉树
{
    若n<=0,返回空指针，递归结束
    创建根节点BT,BT->data=*pre;
    查找根节点在中序序列的位置k；
    创建左子树：BT->lchild=CreateBT(pre+1.in,k)
    创建右子树：BT->rchild=CreateBT(pre+k+1,in+k+1,n-k-1)
    返回BT
}

2.23代码截图

2.24 PTA提交列表说明

分析：虽然该题是一遍过，但是还是有需要注意的地方，就是创建左右子树的递归式的参数，左子树的先序要进一位pre+1，中序序列依旧是原来的in，长度k是中序序列中根节点的位置，右子树的先序是除根节点和左子树剩下的部分所以是pre+k+1，中序是根节点右半部分所以是in+k+1,长度是n-k-1

2.31题目：二叉树叶子结点带权路径长度和

2.32 设计思路（伪代码或流程图）

BTNode *trans(string a,int i,int maxsize)//顺序结构转链式结构
{
    if(i>字符串长度maxsize-1||i<=0) return NULL
    if(a[i]=='#') return NULL
    创建根节点BT，BT->data=a[i]
    创建左子树:BT->lchild=trans(a,2*i,maxsize)
    创建右子树:BT->rchild=trans(a,2*i+1,maxsize)
    返回BT
}
int hfmswpl(BTNode* FBT,int h)//叶子结点带权路径长度和
{
    if(FBT为空) return 0 递归结束
    esle{
                if(FBT是叶子结点)
                {   
                         求和:sum=sum+FBT->data*h   (sum为全局变量int型，初值为0)
                }
                左子树递归:hfmswpl(FBT->lchild,h+1)
                右子树递归:hfmswpl(FBT->rchild,h+1)        
}

2.33代码截图

2.34 PTA提交列表说明

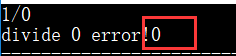
部分正确:

图1是之前if判断的条件语句，发现其实有效长度是除第一个'#'外的其余字符，所以应该i>maxsize-1如图2,发现改正后答案正确

3.截图本周题目集的PTA最后排名

3.1 PTA排名

3.2 我的得分：230

4. 阅读代码

void levelnumber(BTNode *b,int h,int a[])
{
	if(b==NULL) return ;
	else
	{
		a[h]++;
		levelnumber(b->lchild,h+1,a);
		levelnumebr(b->rchild,h+1,a);
	}
}
int fun(BTNode *b)
{
	int width=0,i;
	int a[MaxSize];
	for(i=1;i<MaxSzie;i++) a[i]=0;
	levelnumber(b,1,a);
	i=1;
	while(a[i]!=0)
	{
		if(a[i]>width) width=a[i];
		i++; 
	}
	return width;
 } 

功能:求二叉树的宽度

优点及过程分析：这是课堂派上的一道题目，个人认为这个方法求二叉树宽度，既灵活巧妙又方便理解，levelnumber函数利用数组a并用高度h作为下标实现了每个高度的结点求和也就是二叉树每一层的宽度，再利用fun函数中调用levelnumber函数取得数组a，接着在数组a中取最大值并返回，完成求二叉树宽度的功能。因为这道题在本次上次考试中出现，而我的做法是建立全局变量数组a，其余方法类似，然后是在主函数里求数组a的最大值，上述代码比我的效率高而且容易理解，fun直接返回宽度。

5. 代码Git提交记录截图