CSP10

T1高科技
鞅的停时定理

T2
我们首先可以看出是线性的
矩阵加速

矩阵乘法不满足乘法交换律，所以$a\times b $ 不等于 \(b\times a\)，也就是说你想让\(a\)的一行乘上\(b\)的一列,就把\(a\)放左边
本题中\(b\)应放左边

点击查看代码

#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
// #define ll long long
#define ull unsigned long long
#define lid (rt<<1)
#define rid (rt<<1|1)
// #define endl '\n'
//#define int long long
#define pb push_back
#define int long long
// #pragma comment(linker, “/STACK:512000000,512000000”) 
using namespace std;
#define ll __int128
long long n,mod;
struct Martix
{
	int n,m;
	ll a[4][4];
	void resize(int a,int b)
	{
		n=a;m=b;
	}
	Martix ()
	{
		memset(a,0,sizeof(a));
	}
	void one()
	{
		for(int i=1;i<=3;i++) a[i][i]=1;
	}
	friend Martix operator *(Martix A,Martix B)
	{
		Martix res;
		memset(res.a,0,sizeof(res.a));
		//res.resize(min(B.n,A.n),min(B.m,A.m));
		for(int i=1;i<=3;i++)
		{
			for(int j=1;j<=3;j++)
				for(int k=1;k<=3;k++)
					res.a[i][j]=(res.a[i][j]+A.a[i][k]*B.a[k][j]%mod)%mod;
		}
		return res;
	}
	void T()
	{
		for(int i=1;i<=3;i++)
		{
			for(int j=1;j<=3;j++)
			{
				cout<<(long long)a[i][j]<<" ";
			}
			cout<<endl;
		}
	}
}a,b;
Martix power(Martix a,Martix b,ll c)
{
	// Martix res;
	// res.one();
	while(c)
	{
		if(c&1)a=b*a;
		c>>=1;
		b=b*b;
	}
	return a;
}
signed main()
{
	speed();
	// freopen("in.in","r",stdin);
	// freopen("out.out","w",stdout);
	cin>>n>>mod;
	a.resize(3,3);
	// a.T();
	// cout<<"&&&&&&&&"<<endl;
	b.resize(3,3);
	a.a[2][1]=a.a[3][1]=1;
	b.a[1][2]=b.a[2][2]=b.a[2][3]=b.a[3][3]=1;
	//a.T();
	for(ll k=10;;k*=10)
	{
		//cout<<k<<endl;
		b.a[1][1]=k%mod;
		//cout<<b.a[1][1]<<endl;
		// b.T();
		if(n<k)
		{
			a=power(a,b,n-k/10+1);
			break;
		}
		 //cout<<k-k/10<<endl;
		a=power(a,b,k-k/10);

		//cout<<"======="<<endl;
		//a.T();
	}
	cout<<(long long)a.a[1][1]<<endl;
	return 0;
}

T3简单题

题目背景

zbw 遇上了一道题，由于他急着去找 qby，所以他想让你来帮他做。

题目描述

给你 \(n,k\) 求下式的值：

\(\sum\limits_{i=1}^n\sum\limits_{j=1}^n(i+j)^kf(\gcd(i,j))\gcd(i,j)\)

其中 \(\gcd(i,j)\) 表示 \(i,j\) 的最大公约数。

\(f\) 函数定义如下：

如果 \(k\) 有平方因子 \(f(k)=0\)，否则 \(f(k)=1\)。

Update:平方因子定义 如果存在一个整数 \(k(k>1),k^2|n\) 则 \(k\) 是 \(n\) 的一个平方因子

请输出答案对 \(998244353\) 取模的值。

输入格式

一行两个整数 \(n,k\)。

输出格式

一行一个整数，表示答案对 \(998244353\) 取模后的值。

样例 #1

样例输入 #1

3 3

样例输出 #1

1216

样例 #2

样例输入 #2

2 6

样例输出 #2

9714

样例 #3

样例输入 #3

18 2

样例输出 #3

260108

样例 #4

样例输入 #4

143 1

样例输出 #4

7648044

提示

测试点	\(n\)	\(k\)
\(1,2\)	\(\leq10^3\)	\(\leq10^3\)
\(3,4\)	\(\leq2 \times 10^3\)	\(\leq10^{18}\)
\(5 \sim8\)	\(\leq5 \times 10^4\)	\(\leq10^{18}\)
\(9\)	\(\leq 5\times10^6\)	\(=1\)
\(10,11\)	\(\leq 5\times10^6\)	\(=2\)
\(12,13\)	\(\leq 5\times10^6\)	\(\leq10^3\)
\(14 \sim20\)	\(\leq 5\times10^6\)	\(\leq10^{18}\)

对于 \(100\%\) 的数据，\(1 \leq n \leq 5 \times 10^6\)，\(1 \leq k \leq 10^{18}\)。

Update on 2020/3/16:

时间调至 \(1\)s,卡掉了 \(O(n\log k)\),\(O(n\log mod)\) 的做法。

首先发现一个性质:我们设\(gcd(i,j)=d\),函数\(f(x)\)即为\(\mu^2(x)\),即为\(\sum_{i=1}^n\sum_{j=1}^n\mu^2(d)d(i+j)^k\)

\[\sum_{d=1}^n\mu^2(d)d\sum_{i=1}^n\sum_{j=1}^n(i+j)^k[gcd(i,j)=d] \]

\[\sum_{d=1}^n\mu^2(d)d^{k+1}\sum_{i=1}^{\lfloor {\frac{n}{d}} \rfloor}\sum_{j=1}^{\lfloor {\frac{n}{d}} \rfloor}(i+j)^k[gcd(i,j)=1] \]

根据\(\sum_{d|n}\mu (d)=[n=1]\)

\[\sum_{d=1}^n\mu^2(d)d^{k+1}\sum_{i=1}^{\lfloor {\frac{n}{d}} \rfloor}\sum_{j=1}^{\lfloor {\frac{n}{d}} \rfloor}(i+j)^k\sum_{t|gcd(i,j)}\mu (t) \]

\[\sum_{d=1}^n\mu^2(d)d^{k+1}\sum_{t=1}^{\lfloor {\frac{n}{d}} \rfloor}\mu(t)t^k\sum_{i=1}^{\lfloor {\frac{n}{dt}} \rfloor}\sum_{j=1}^{\lfloor {\frac{n}{dt}} \rfloor}(i+j)^k \]

然后我们肯定不能\(O(n^3)\)的去处理，最左边\(\sum_{d=1}^n\mu^2(d)d^{k+1}\)和\(\sum_{t=1}^{\lfloor {\frac{n}{d}} \rfloor}\mu(t)t^k\sum_{i=1}^{\lfloor {\frac{n}{dt}} \rfloor}\)我们可以\(O(n)\)预处理出来,最后一部分如何做到\(O(n)\)预处理呢?
画一下图

^
7|
6|
5|
4|5 6 7 8
3|4 5 6 7
2|4 5 5 6
1|2 3 4 5
.------------------->
  1 2 3 4 5 6 7 8 9

设\(t(x)=x^k,sum(x)=\sum_{i=1}^x i^k\)发现\(t(x)=t(x-1)+2\times(sum(2i-1)-sum(i))+sum(2i)-sum(2i-1)\)
好了剩下的怎么办，用数列分块就可以啦,计算次方可以用扩展欧拉定理!

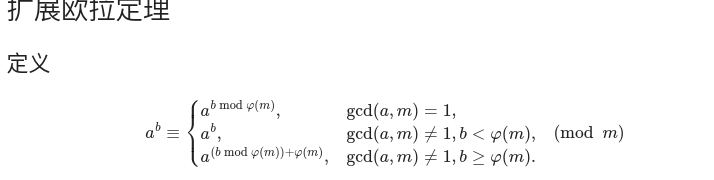
点击查看代码

#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define ull unsigned long long
#define lid (rt<<1)
#define rid (rt<<1|1)
// #define endl '\n'
//#define int long long
#define pb push_back
// #pragma comment(linker, “/STACK:512000000,512000000”) 
using namespace std;
const int N = 5e6+5,mod=998244353;
ll n,k;int mu[N],pr[N],tot;bool is[N];
inline ll qpow(ll a,ll b)
{
	ll ans=1;
	while(b)
	{
		if(b&1)ans=ans*a%mod;
		a=a*a%mod;
		b>>=1;
	}
	return ans;
}
void getMu()
{
	mu[1]=1;
	for(register int i=2;i<=n;i=-~i)
	{
		if(!is[i])
		{
			pr[++tot]=i;mu[i]=-1;
		}
		for(register int j=1;j<=tot&&i*pr[j]<=n;j=-~j)
		{
			is[i*pr[j]]=1;
			if(i%pr[j]==0)
			{
				mu[i*pr[j]]=0;break;
			}
			mu[i*pr[j]]=-mu[i];
		}
	}
}
ll ud[N],td[N],tt[N];int sp[N*2],p[N*2];
inline ll slfk(ll x)
{
	ll res=0;
	register int l=1,r;
	while(l<=x)
	{
		r=x/(x/l);
		res=(1ll*(td[r]-td[l-1]+mod)%mod*tt[x/l]+res)%mod;
		l=r+1;
	}
	return res;
}
inline ll slfk2(ll x)
{
	ll res=0;
	register ll l=1,r;
	while(l<=x)
	{
		r=x/(x/l);
		ll rres=slfk(x/l);
		res=(1ll*(ud[r]-ud[l-1]+mod)%mod*rres+res)%mod;
		l=r+1;
	}
	return res;
}
signed main()
{
	speed();
	// freopen("in.in","r",stdin);
	// freopen("out.out","w",stdout);
	cin>>n>>k;
	// cout<<"**************8"<<endl;
	getMu();
	p[1]=1;
	for(int i=2;i<=2*n;i=-~i)//O(2e8)
	{
		p[i]=qpow(i,k%(mod-1));
		sp[i]=(sp[i-1]+p[i])%mod;
		// cout<<sp[i]<<endl;
	}
	for(ll d=1;d<=n;d=-~d)
	{
		ud[d]=(ud[d-1]+mu[d]*mu[d]*p[d]*d%mod)%mod;
	}
	for(ll t=1;t<=n;t=-~t)
	{
		td[t]=(td[t-1]+mu[t]*p[t])%mod;
	}
	tt[1]=p[2];
	for(int i=2;i<=n;i=-~i)
	{
		tt[i]=(tt[i-1]+2*(sp[2*i-1]-sp[i])%mod+p[2*i])%mod;
	}
	ll ans=0;
	ans=slfk2(n)%mod;
	cout<<ans;
	return 0;
}
/*
^
7|
6|
5|
4|5 6 7 8
3|4 5 6 7
2|4 5 5 6
1|2 3 4 5
.------------------->
  1 2 3 4 5 6 7 8 9
*/

当然，还没完,学校题库怎么可能过得去呢（跑那么慢）
预处理\(i^k\)的复杂度为\(O(nlogn)\)我们可以放进线性筛中

点击查看代码

#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define ull unsigned long long
#define lid (rt<<1)
#define rid (rt<<1|1)
// #define endl '\n'
//#define int long long
#define pb push_back
// #pragma comment(linker, “/STACK:512000000,512000000”) 
using namespace std;
const int N = 5e6+5,mod=998244353;
ll n,k;int mu[N],pr[N],tot;bool is[N*2];
int sp[N*2];
inline ll qpow(ll a,ll b)
{
	ll ans=1;
	while(b)
	{
		if(b&1)ans=ans*a%mod;
		a=a*a%mod;
		b>>=1;
	}
	return ans;
}
void getMu()
{
	mu[1]=1;
	for(register int i=2;i<=2*n;i=-~i)
	{
		if(!is[i])
		{
			pr[++tot]=i;
			if(i<=n)mu[i]=-1;
			sp[i]=qpow(i,k);
		}
		for(register int j=1;j<=tot&&i*pr[j]<=2*n;j=-~j)
		{
			is[i*pr[j]]=1;
			sp[i*pr[j]]=1ll*sp[i]*sp[pr[j]]%mod;
			if(i%pr[j]==0)
			{
				break;
			}
			if(i*pr[j]<=n)mu[i*pr[j]]=-mu[i];
		}
	}
}
ll ud[N],td[N],tt[N];
inline ll slfk(ll x)
{
	ll res=0;
	register int l=1,r;
	while(l<=x)
	{
		r=x/(x/l);
		res=(1ll*(td[r]-td[l-1]+mod)%mod*tt[x/l]+res)%mod;
		l=r+1;
	}
	return res;
}
inline ll slfk2(ll x)
{
	ll res=0;
	register ll l=1,r;
	while(l<=x)
	{
		r=x/(x/l);
		ll rres=slfk(x/l);
		res=(1ll*(ud[r]-ud[l-1]+mod)%mod*rres+res)%mod;
		l=r+1;
	}
	return res;
}
signed main()
{
	speed();
	// freopen("in.in","r",stdin);
	// freopen("out.out","w",stdout);
	cin>>n>>k;
	// cout<<"**************8"<<endl;
	getMu();
	sp[1]=1;
	for(int i=2;i<=2*n;i=-~i)//O(2e8)
	{
		// p[i]=qpow(i,k%(mod-1));
		sp[i]=1ll*(sp[i-1]+sp[i])%mod;
		// cout<<sp[i]<<endl;
	}
	for(ll d=1;d<=n;d=-~d)
	{
		ud[d]=1ll*(ud[d-1]+1ll*mu[d]*mu[d]*(sp[d]-sp[d-1])*d%mod)%mod;
	}
	for(ll t=1;t<=n;t=-~t)
	{
		td[t]=1ll*(td[t-1]+1ll*mu[t]*(sp[t]-sp[t-1]))%mod;
	}
	tt[1]=sp[2]-sp[1];
	for(int i=2;i<=n;i=-~i)
	{
		tt[i]=1ll*(tt[i-1]+2*(sp[2*i-1]-sp[i])%mod+(sp[2*i]-sp[2*i-1])%mod+mod)%mod;
	}
	ll ans=0;
	ans=slfk2(n)%mod;
	cout<<(ans+mod)%mod;
	return 0;
}
/*
^
7|
6|
5|
4|5 6 7 8
3|4 5 6 7
2|4 5 5 6
1|2 3 4 5
.------------------->
  1 2 3 4 5 6 7 8 9
*/

加强版看这里