返回顶部

暑假集训CSP提高模拟8

T1
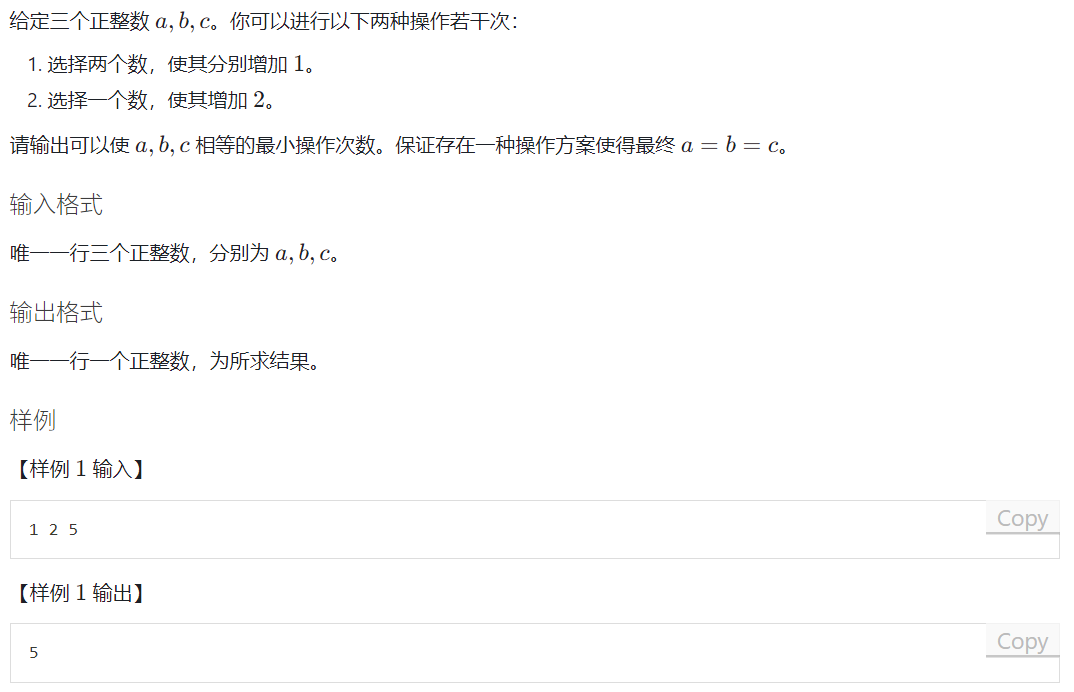
image

点击查看代码 
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll a[5];
int main()
{
	cin>>a[1]>>a[2]>>a[3];
	sort(a+1,a+3+1);
	ll ans=(a[3]-a[1])/2+(a[3]-a[2])/2;
	a[1]+=(a[3]-a[1])/2*2;a[2]+=(a[3]-a[2])/2*2;
	if(a[1]==a[2]&&a[1]!=a[3])ans++;
	else if(a[1]!=a[2])ans+=2;
	cout<<ans;
	return 0;
}

T2
赛时想法是维护\(m\)个并查集,二分答案,然后比较祖先是否相同,\(O(mlogn+qmlogn)\)的复杂度,而且内存开不下，只拿\(20pts\)

点击查看代码 
#include <bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int N = 1e5+5;
vector <int> fa[N*2];
vector <pair<int,int>> G;
int n,m,q;
inline int find(int u,int id)
{
	if(fa[id][u]!=u)fa[id][u]=find(fa[id][u],id);
	return fa[id][u];
}
inline bool check(int mid,int L,int R)
{
	int c=find(L,mid);
//	cout<<c<<endl;
	for(int i=L+1;i<=R;i++)
	{
		if(find(i,mid)!=c)return 0;
	}
	
	return 1;
}
inline int fen(int l,int r,int L,int R)
{
	int ans=0;
	while(l<=r)
	{
		int mid=(l+r)>>1;
		if(check(mid,L,R))
		{
			ans=mid;
			r=mid-1;
		}else
		{
			l=mid+1;
		}
	}
	return ans;
}
inline void work1()
{
	int u,v;
	for(int i=0;i<=m;i++)fa[i].resize(n+1);
	for(int i=1;i<=n;i++)fa[0][i]=i;
	for(int i=1;i<=m;i++)
	{
		copy(fa[i-1].begin(),fa[i-1].end(),fa[i].begin());
		u=G[i].first,v=G[i].second;
		int fu=find(u,i),fv=find(v,i);
		if(fu!=fv)fa[i][fu]=fv;
	}
	int l,r;
	while(q--)
	{
		cin>>l>>r;
		if(l==r)cout<<0<<endl;
		else
		{
			cout<<fen(1,m,l,r)<<endl;
		}
	}
}
int w2(int l,int r,int L,int R)
{
	int ans=0;
	while(l<=r)
	{
		int mid=(l+r)>>1;
		if(check(0,L,R))
		{
			ans=mid;
			r=mid-1;
		}else
		{
			l=mid+1;
		}
	}
	return ans;
}
void work2()
{
	int l,r;
	cin>>l>>r;
//	cout<<l<<" "<<r<<endl;
	int u,v;
	fa[0].resize(n+1);
	for(int i=1;i<=n;i++)fa[0][i]=i;
	for(int i=1;i<=m;i++)
	{
		u=G[i].first,v=G[i].second;
		int fu=find(u,0),fv=find(v,0);
		if(fu!=fv)fa[0][fu]=fv;
//		if(i>=r-l+1)
//		{
		if(check(0,l,r))
		{
			cout<<i<<endl;
			break;
		}
//		}
//		cout<<fu<<" "<<fv<<endl;
	}	
}
int main()
{
	ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);	
//	freopen("lagrange2.in","r",stdin);
	
	cin>>n>>m>>q;int u,v;G.pb({0,0});
	for(int i=1;i<=m;i++)
	{
		cin>>u>>v;G.pb({u,v});
	}
	if(n<=100&&m<=100)
	{
		work1();
	}else if(q==1)
	{
//		cout<<"*****"<<endl;
		work2();
	}else
	{
		work1();
	}
	return 0;
}

暴力部分分可以拿到\(35pts\)

点击查看代码 
#include <bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int N = 1e5+5;
vector <pair<int,int>> edge[N];
int n,m,q;bool vis[N];
void dfs(int u,int fa,int lim)
{
	vis[u]=1;
//	cout<<u<<endl;
	for(int i=0;i<edge[u].size();i++)
	{
		int to=edge[u][i].first,id=edge[u][i].second;
		if(id>lim)continue;
		if(to==fa||vis[to])continue;
//		cout<<to<<" "<<u<<" "<<lim<<endl;
		dfs(to,u,lim);
	}
}
bool check(int mid,int L,int R)
{
//	cout<<"CHECK"<<mid<<" "<<L<<" "<<R<<endl;
	
//	for(int i=L;i<=R;i++)vis[i]=0;
	memset(vis,0,sizeof vis);
	dfs(L,0,mid);
	for(int i=L;i<=R;i++)
	{
		if(!vis[i])return 0;
	}
	return 1;
}
int fen(int l,int r,int L,int R)
{
	int ans=0;
	while(l<=r)
	{
		int mid=(l+r)>>1;
		if(check(mid,L,R))
		{
			ans=mid;
			r=mid-1;
		}else
		{
			l=mid+1;
		}
	}
	return ans;
}
int main()
{
	ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);	
//	freopen("lagrange2.in","r",stdin);
	
	cin>>n>>m>>q;int u,v;
	for(int i=1;i<=m;i++)
	{
		cin>>u>>v;
//		cout<<"***"<<u<<" "<<v<<endl;
		edge[u].pb({v,i});
		edge[v].pb({u,i});
	}
	int l,r;
	while(q--)
	{
		cin>>l>>r;
		if(l==r)cout<<0<<endl;
		else
		{
			cout<<fen(1,m,l,r)<<endl;
		}
	}
	return 0;
}

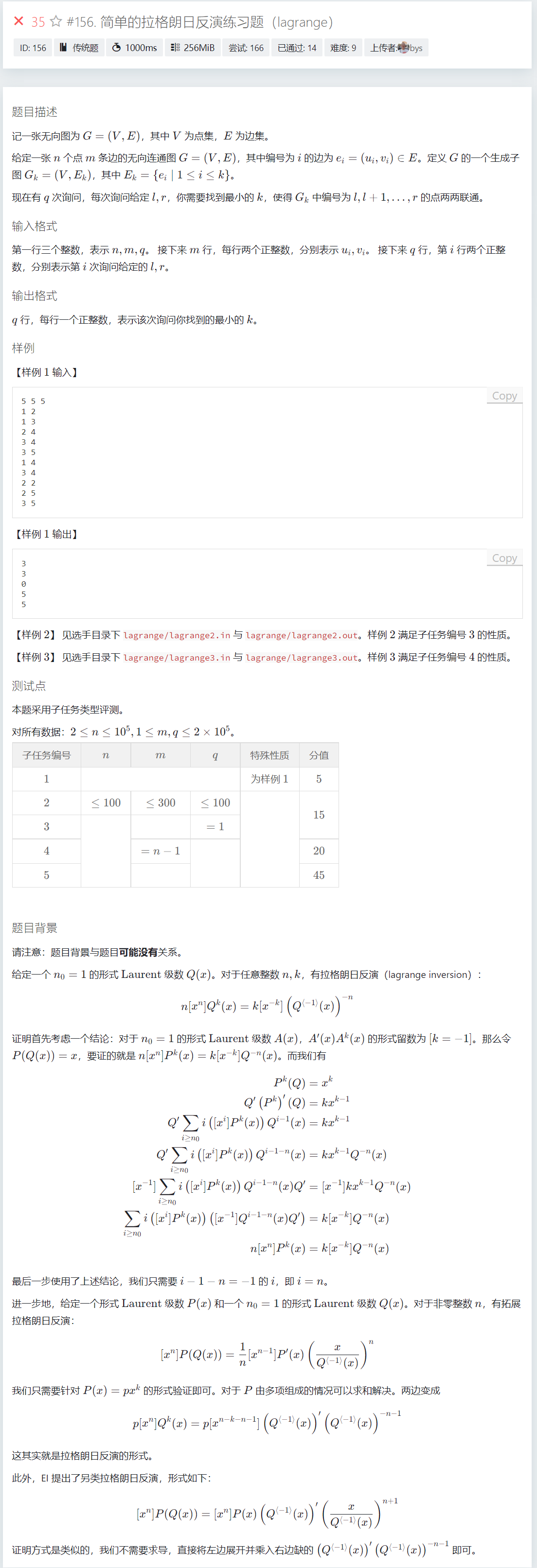
image

正解，\(Kruskal\)重构树,边的编号即为边权,我考试并查集想到了，\(kruskal\)没想到，哎
image
image

其实\(m==n-1\)就是在启发树的时候如何处理，
我们想要知道\([l,r]\)即为\(l->r\)的边权最大值,相当于\(max(l->l+1,l+1->l+2,...，r-1->r)\),所以我们可以预处理出全部的\((i,i+1)\),然后查询可以用线段树，\(ST表\),查询\([l,r-1]\)即可

点击查看代码 
#include <bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int N = 1e5+5;
//vector <pair<int,int>> edge[N];
int n,m,q,fa[N*2],f[N*2][25],now,st[N][25],val[N*3],dep[N*2];bool vis[N*3];
struct Node{int u,v,w;};vector <Node> G ;
//bool cmp(Node a,Node b){return a.w<b.w;}
vector <int> edge[N*2];
int find(int u)
{
	if(fa[u]!=u)fa[u]=find(fa[u]);
	return fa[u];
}
void dfs(int u,int fa)
{
	vis[u]=1;
	dep[u]=dep[fa]+1;
	f[u][0]=fa;
	for(int j=1;j<=20;j++)
		f[u][j]=f[f[u][j-1]][j-1];
	for(auto to:edge[u])
	{
		if(to==fa)continue;
		dfs(to,u);	
	}	
}
int lca(int x,int y)
{
	if(dep[x]<dep[y])swap(x,y);
	for(int j=20;j>=0;j--)
		if(dep[f[x][j]]>=dep[y])x=f[x][j];
	if(x==y)return x;
	for(int i=20;i>=0;i--)
		if(f[x][i]!=f[y][i])
			x=f[x][i],y=f[y][i];
	return f[x][0];
}
void ST()
{
	for(int i=2;i<=n;i++)
	{
		st[i][0]=val[lca(i-1,i)];
//		cout<<"*&&&"<<lca(i,i+1)<<" "<<val[lca(i,i+1)]<<endl;
	}
	
	for(int j=1;j<=20;j++)
	{
		for(int i=1;i+(1<<j)-1<=n;i++)
		{
			st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
		}
	}
}
int query(int l,int r)
{
	int k=log2(r-l+1);
	return max(st[l][k],st[r-(1<<k)+1][k]);
}
void kruskal()
{
	for(int i=1;i<=2*n;i++)fa[i]=i;
	now=n;
	for(int i=1;i<=m;i++)
	{
		int fu=find(G[i].u),fv=find(G[i].v);
		if(fu!=fv)
		{
			++now;val[now]=G[i].w;
			fa[fv]=now;fa[fu]=now;
			edge[now].pb({fu});
			edge[now].pb({fv});
		}
	}
	dfs(now,0);
//	for(int i=now;i;i--)
//		if(!vis[i])dfs(i,0);
//	n*=2;
	ST();
}

int main()
{
	ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);	
//	freopen("lagrange2.in","r",stdin);
	
	cin>>n>>m>>q;int u,v;G.pb({0,0});
	for(int i=1;i<=m;i++)
	{
		cin>>u>>v;
		G.pb({u,v,i});
	}
	kruskal();
	int l,r;
	while(q--)
	{
		cin>>l>>r;
		if(l==r)cout<<0<<endl;
		else
		{
			cout<<query(l+1,r)<<endl;
		}
	}
	return 0;
}

T3

T4朴素的抽象代数题（algebra）

题目背景

众所周知，抽象代数中研究的一种重要的群，就是置换群。在本题中，我们就将探索抽象代数和置换的奥秘。

记小写字母集合的确定子集为 \(\mathbb L\)。

定义在 \(\mathbb L\) 上的映射为一个双射 \(f: \mathbb L \rightarrow \mathbb L\)。容易发现，可以将一个映射 \(f\) 记作一个长度为 \(|\mathbb L|\) 的排列 \(f\)，令第 \(i\) 个字母被映射为第 \(f_i\) 个字母。（为方便起见，给出的排列均为 \(0 \sim |\mathbb L| - 1\) 的排列）

定义一个恒等映射为满足所有字母被映射到其本身的映射。

记字符 \(s\) 在 \(f\) 下的像为 \(f(s)\)。记一个字符串 \(S\) 的第 \(i\) 个字符为 \(S[i]\)。

定义映射 \(f\) 对字符串 \(S\) 的操作 \(f(S)\) 为将字符串内每个元素 \(S[i]\) 替换为 \(f(S[i])\)。
例如，当 \(\mathbb L = \{\text{a},\text{b},\text{c}\}\)，\(f = \{ 1,2,0 \}\)，\(S = \text{abcac}\) 时，\(f(S) = \text{bcaba}\) 。

定义映射的复合运算 \(\circ\) 按如下方式给出 \(c = a\circ b\)：

\[\forall\ s\in \mathbb{L},\ c(s) = b(a(s)) \]

例如，当 \(\mathbb L = \{\text{a},\text{b},\text{c}\}\)，\(f = \{ 1,2,0 \}\)，\(g = \{ 0,2,1 \}\) 时，存在 \(h = f\circ g = \{2,1,0\}\) 满足条件。
容易发现对确定的 \(a,b\)，只存在一个 \(c\) 满足条件。

题目描述

给定 \(\mathbb L\) 的大小 \(l\)，\(\mathbb L = \{\) 前 \(l\) 个小写字母 \(\}\)。

给定循环节大小为 \(n\) 的无限长操作序列与 \(m\) 个映射，第 \(i\) 个映射被编号为 \(f_i\)。你有一个映射 \(f_0\)，其初始时是恒等映射。

第 \(i\) 次操作有两种可能的情况：

  1. 为一个数字 \(k\)，保证 \(k \in [1,m]\)。

    将 \(f_k\) 复合到 \(f_0\) 上。
    具体地，我们操作 \(f_0 \leftarrow f_0 \circ f_k\)。

  2. 为一个字符串 \(S\)，保证其由 \(\in \mathbb{L}\) 的元素组成。

    记录下 \(f_0(S)\)。

现在有 \(q\) 次询问，每次询问给定 \(x\)，你需要输出第 \(x\) 次记录下的字符串。

输入格式

为避免大量输入输出带来的时空损耗，本题实际输入采用 xorShift128Plus 算法生成，该算法所需各参数为输入文件中所含内容，格式于下方给出。

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
ull n, m, q, l, STR_LEN, seed1, seed2, FREQ, MAX_X;
int f[26], LEN;

ull xorShift128Plus() {
    ull k3 = seed1, k4 = seed2;
    seed1 = k4;
    k3 ^= (k3 << 23);
    seed2 = k3 ^ k4 ^ (k3 >> 17) ^ (k4 >> 26);
    return seed2 + k4;
}

signed main() {
    scanf("%llu %llu %llu %llu %llu %llu %llu %llu %llu", 
            &n, &m, &q, &l, &seed1, &seed2, &STR_LEN, &FREQ, &MAX_X);
    seed1 = xorShift128Plus() * xorShift128Plus();
    seed2 = xorShift128Plus() * xorShift128Plus();
    mt19937 rnd(seed1 * seed2);

    for (int i = 0; i < l; i++) f[i] = i;
    for (int i = 1; i <= m; i++) {
        shuffle(f, f + l, rnd);
        for (int i = 0; i < l; i++) {
            printf("%d ", f[i]);
        } putchar('\n');
    }

    for (int i = 1; i <= n; i++) {
        if (xorShift128Plus() % FREQ <= 1) {
            printf("%llu ", xorShift128Plus() % m + 1);
        } else {
            LEN = STR_LEN - (xorShift128Plus() & 7);
            for (int i = 1; i <= LEN; i++) {
                printf("%c", (char)(xorShift128Plus() % l + 'a'));
            } putchar(' ');
        } 
    } putchar('\n');

    for (int i = 1; i <= q; i++) {
        printf("%llu\n", xorShift128Plus() % MAX_X + 1);
    }
	return 0;
}

该程序输出内容（实际输入）的意义如下：

  1. \(m\) 行，第 \(i\) 行 \(l\) 个整数表示第 \(i\) 个置换。
  2. 一行 \(n\) 个字符串或数字表示操作序列。
  3. \(q\) 行，第 \(i\) 行一个整数表示第 \(i\) 次询问的 \(x\)。

输入文件中仅包含一行九个整数，分别为 \(n, m, q, l, \text{seed1}, \text{seed2}, \text{STR\_LEN}, \text{FREQ}, \text{MAX\_X}\) 。

输出格式

为避免大量输入输出带来的时空损耗，本题使用特殊方法输出。

定义哈希函数 \(\text{getHash}(ch)\) 如下：

typedef unsigned long long ull;
ull getHash(char ch[]) {
    ull hsh = 0; int len = strlen(ch + 1);
    for (int i = 1; i <= len; i++) hsh = hsh * 131 + ch[i];
    return hsh;
}

设第 \(i\) 次输出的字符串为 \(S_i\)。形式化地，你需要输出

\[\bigoplus_{i = 1}^q \ (\text{getHash}(S_i) - i) \text{ mod } 2^{64} \]

的值，即所有 \(\text{getHash}(S_i) - i\) 模 \(2^{64}\) 所得值的异或和。

样例

【样例 \(1\) 输入】

10 5 20 10 114514 1919810 10 4 100

【样例 \(1\) 输出】

1303754058526545

【样例 \(2\)】
见选手目录下 segment/segment2.in 与 segment/segment2.out。样例 \(2\) 满足测试点编号 \(6\sim 10\) 的性质。

测试点

对所有数据：\(1 \le n, m \le 10^6\)，\(1 \le q \le 10^6\)，\(2 \le l \le 26\)，\(1 \le x \le 10^{18}\)，\(8 \le \text{STR\_LEN} \le 50\)，\(1 \le \text{FREQ} \le 40\)，\(\text{seed1, seed2}\) 可通过 unsigned long long 型变量保存。

测试点编号 \(n, m\) \(q\) \(l\) \(x\)
\(1\) \(10\) \(100\) \(10\) \(100\)
\(2\sim 5\) \(10^3\) \(10^3\) \(20\) \(10^5\)
\(6\sim 10\) \(10^5\) \(10^5\) \(10^9\)
\(11\sim 20\)
posted @ 2024-07-26 20:08  wlesq  阅读(9)  评论(0)  编辑  收藏  举报