聪聪与可可

[NOI2005] 聪聪与可可

题目描述

在一个魔法森林里，住着一只聪明的小猫聪聪和一只可爱的小老鼠可可。虽然灰姑娘非常喜欢她们俩，但是，聪聪终究是一只猫，而可可终究是一只老鼠，同样不变的是，聪聪成天想着要吃掉可可。

一天，聪聪意外得到了一台非常有用的机器，据说是叫 GPS，对可可能准确的定位。有了这台机器，聪聪要吃可可就易如反掌了。于是，聪聪准备马上出发，去找可可。而可怜的可可还不知道大难即将临头，仍在森林里无忧无虑的玩耍。小兔子乖乖听到这件事，马上向灰姑娘报告。灰姑娘决定尽快阻止聪聪，拯救可可，可她不知道还有没有足够的时间。

整个森林可以认为是一个无向图，图中有 \(N\) 个美丽的景点，景点从 \(1\) 至 \(N\) 编号。小动物们都只在景点休息、玩耍。在景点之间有一些路连接。

当聪聪得到 GPS 时，可可正在景点 \(M\)（\(M \le N\)）处。以后的每个时间单位，可可都会选择去相邻的景点（可能有多个）中的一个或停留在原景点不动。而去这些地方所发生的概率是相等的。假设有 \(P\) 个景点与景点 \(M\) 相邻，它们分别是景点 \(R\)、景点 \(S\)、……、景点 \(Q\)，在时刻 \(T\) 可可处在景点 \(M\)，则在 \((T+1)\) 时刻，可可有 \(1/(1 +P)\) 的可能在景点 \(R\)，有 \(1/(1 +P)\) 的可能在景点 \(S\)，……，有 \(1/(1 +P)\) 的可能在景点 \(Q\)，还有\(1/(1 +P)\)的可能停在景点 \(M\)。

我们知道，聪聪是很聪明的，所以，当她在景点 \(C\) 时，她会选一个更靠近可可的景点，如果这样的景点有多个，她会选一个标号最小的景点。由于聪聪太想吃掉可可了，如果走完第一步以后仍然没吃到可可，她还可以在本段时间内再向可可走近一步。

在每个时间单位，假设聪聪先走，可可后走。在某一时刻，若聪聪和可可位于同一个景点，则可怜的可可就被吃掉了。

灰姑娘想知道，平均情况下，聪聪几步就可能吃到可可。而你需要帮助灰姑娘尽快的找到答案。

输入格式

数据的第 1 行为两个整数 \(N\) 和 \(E\)，以空格分隔，分别表示森林中的景点数和连接相邻景点的路的条数。

第 2 行包含两个整数 \(C\) 和 \(M\)，以空格分隔，分别表示初始时聪聪和可可所在的景点的编号。

接下来 E 行，每行两个整数，第 \(i+2\) 行的两个整数 \(A_i\) 和 \(B_i\) 表示景点 \(A_i\) 和景点 \(B_i\) 之间有一条路。所有的路都是无向的，即：如果能从 A 走到 B，就可以从 B 走到 A。

输入保证任何两个景点之间不会有多于一条路直接相连，且聪聪和可可之间必有路直接或间接的相连。

输出格式

输出 1 个实数，四舍五入保留三位小数，表示平均多少个时间单位后聪聪会把可可吃掉。

样例 #1

样例输入 #1

样例输出 #1

1.500

样例 #2

样例输入 #2

样例输出 #2

2.167

提示

【样例说明 1】

开始时，聪聪和可可分别在景点 1 和景点 4。

第一个时刻，聪聪先走，她向更靠近可可(景点 4)的景点走动，走到景点 2，然后走到景点 3；假定忽略走路所花时间。

可可后走，有两种可能：第一种是走到景点 3，这样聪聪和可可到达同一个景点，可可被吃掉，步数为 \(1\)，概率为\(0.5\)。

第二种是停在景点 4，不被吃掉。概率为 \(0.5\)。

到第二个时刻，聪聪向更靠近可可(景点 4)的景点走动，只需要走一步即和可可在同一景点。因此这种情况下聪聪会在两步吃掉可可。所以平均的步数是 \(1\times 1/2 + 2\times 1/2 =1.5\) 步。

【样例说明 2】

森林如下图所示：

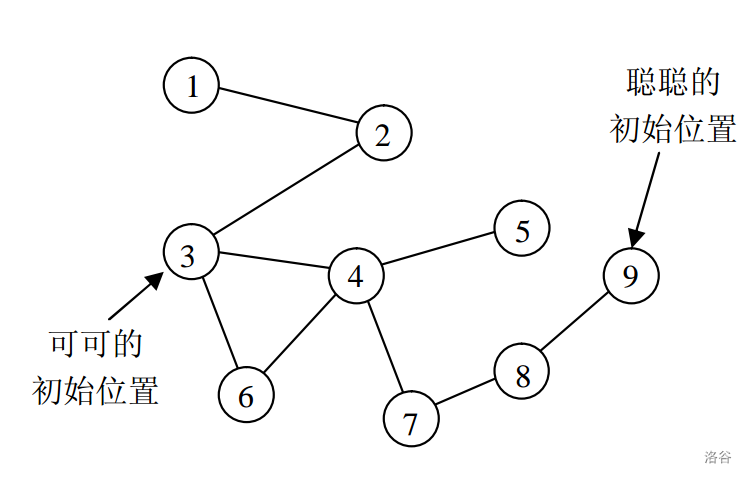
对于 50%的数据，\(1≤N≤50\)。
对于所有的数据，\(1≤N,E≤1000\)。

这题思想真的很神奇，因为他们所在的点是来回移动的，终点也是，有很多为未知性，所以为了让记忆化搜索方便，我们可以预先处理出猫从i点出发到达各点的距离
分析题目，找出一些细节：
猫可以走一步或两步；
老鼠可以不动；
猫必须走到离老鼠最近的点，如距离有相同，则选编号最小的点。
然后我们可以预处理出猫在点i，老鼠在点j，猫的下一个走位\(nxt[i][j]\)
怎么预处理出\(nxt[i][j]\)
提供两种思路，一种使用DIJ/SPFA ,然后处理出\(nxt[i][j]\)如何预处理呢?
首先i的下一步必为to,但是to必须能到达k所以\(dis[i][k]==dis[to][k]+1\)时才能转移，注意取最小的的
预处理完了，然后如何记忆化搜索呢?
起点是c和m,猫可以走一步或两步

double dfs(int u,int v)
{	
	if(hav[u][v])return f[u][v];
	if(u==v)return 0;
	int one=nxt[u][v];
	int two=nxt[one][v];
	if(one==v||two==v)return 1;//如果一两步能到，则概率为1
	f[u][v]=1;
	for(int i=head[v];i;i=edge[i].next)
	{
		int to=edge[i].to;
		if(dis[to][v]!=inf)
		{
			f[u][v]+=(D)dfs(two,to)/(D)(in[v]+1);加上不动的情况

		}
	}
	f[u][v]+=(D)dfs(two,v)/(D)(in[v]+1);
	hav[u][v]=1;
	return f[u][v];
}

注意\(f[u][v]=1\)
通俗来讲就是花费了1的时间，所以要加1

点击查看代码

#include <bits/stdc++.h>
#define ll long long
#define D double
#define rint int
#define mk make_pair
#define pb push_back
#define lid (rt<<1)
#define rid (rt<<1|1)
using namespace std;
const int N = 2005,inf=0x3f3f3f3f;
int n,e,c,m,cnt,head[N];
struct Edge
{
	int u,to,w,next;
}edge[N*2];
void add(int u,int v)
{
	edge[++cnt].u=u;
	edge[cnt].to=v;
	edge[cnt].next=head[u];
//	edge[cnt].w=w;
	head[u]=cnt;
}
int in[N],out[N],dis[N][N],nxt[N][N];
double f[N][N];bool vis[N];
inline void dij(int id,int st)
{
	for(int i=0;i<=n;i++)vis[i]=0;
	priority_queue <pair<int,int>,vector<pair<int,int>>,less<pair<int,int>> > q;
	q.push(mk(0,st));
	dis[id][st]=0;
	while(q.size())
	{
		int u=q.top().second;q.pop();
		if(vis[u])continue;
		vis[u]=1;
		for(int i=head[u];i;i=edge[i].next)
		{
			int to=edge[i].to;
			if(dis[id][to]>dis[id][u]+1)
			{
				dis[id][to]=dis[id][u]+1;
//				cout<<id<<" "<<to<<" "<<dis[id][to]<<endl;
				q.push(mk(-dis[id][to],to));
			}
		}
	}
}
bool hav[N][N];
double dfs(int u,int v)
{	
//	cout<<u<<" "<<v<<endl;
	if(hav[u][v])return f[u][v];
	if(u==v)return 0;
	int one=nxt[u][v];
////	cout<<u<<" "<<one<<endl;
	int two=nxt[one][v];
//	cout<<u<<" "<<v<<endl;
	if(one==v||two==v)return 1;
	f[u][v]=1;
//	cout<<u<<" "<<v<<endl;
	for(int i=head[v];i;i=edge[i].next)
	{
		int to=edge[i].to;
		if(dis[to][v]!=inf)
		{
			f[u][v]+=(D)dfs(two,to)/(D)(in[v]+1);
//			cout<<u<<" "<<v<<" "<<f[u][v]<<endl;
		}
	}
	f[u][v]+=(D)dfs(two,v)/(D)(in[v]+1);
	hav[u][v]=1;
	return f[u][v];
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
//	freopen("P4206_4.in","r",stdin);
//	freopen("A.out","w",stdout);
//	memset(f,-1,sizeof(f));
	cin>>n>>e;
	cin>>c>>m;
	int a,b;
	for(int i=1;i<=e;i++)
	{
		cin>>a>>b;
		add(a,b);
		add(b,a);
		in[a]++;in[b]++;
	}
//	cout<<"??"<<endl;
	for (int i=1;i<=n;i++)
	{
		for (int j=1;j<=n;j++)
		{
			dis[i][j]=inf;
			nxt[i][j]=inf;
		}
			
	}
//	cout<<"??"<<endl;
	for(int i=1;i<=n;i++)
	{
		dij(i,i);
	}
	for (int i=1;i<=n;i++)
	{
		for(int j=head[i];j;j=edge[j].next)
		{
			int to=edge[j].to;
			for(int k=1;k<=n;k++)
			{
				if(dis[i][k]==dis[to][k]+1)
				{
					nxt[i][k]=min(nxt[i][k],to);
				}
			}			
		}
	}

	printf("%.3f",dfs(c,m));
	return 0;
}

BFS版