OKR-Periods of Words

[POI2006] OKR-Periods of Words

题面翻译

对于一个仅含小写字母的字符串 \(a\)，\(p\) 为 \(a\) 的前缀且 \(p\ne a\)，那么我们称 \(p\) 为 \(a\) 的 proper 前缀。

规定字符串 \(Q\) 表示 \(a\) 的周期，当且仅当 \(Q\) 是 \(a\) 的 proper 前缀且 \(a\) 是 \(Q+Q\) 的前缀。若这样的字符串不存在，则 \(a\) 的周期为空串。

例如 ab 是 abab 的一个周期，因为 ab 是 abab 的 proper 前缀，且 abab 是 ab+ab 的前缀。

求给定字符串所有前缀的最大周期长度之和。

题目描述

A string is a finite sequence of lower-case (non-capital) letters of the English alphabet. Particularly, it may be an empty sequence, i.e. a sequence of 0 letters. By A=BC we denotes that A is a string obtained by concatenation (joining by writing one immediately after another, i.e. without any space, etc.) of the strings B and C (in this order). A string P is a prefix of the string !, if there is a string B, that A=PB. In other words, prefixes of A are the initial fragments of A. In addition, if P!=A and P is not an empty string, we say, that P is a proper prefix of A.

A string Q is a period of Q, if Q is a proper prefix of A and A is a prefix (not necessarily a proper one) of the string QQ. For example, the strings abab and ababab are both periods of the string abababa. The maximum period of a string A is the longest of its periods or the empty string, if A doesn't have any period. For example, the maximum period of ababab is abab. The maximum period of abc is the empty string.

Task Write a programme that:

reads from the standard input the string's length and the string itself,calculates the sum of lengths of maximum periods of all its prefixes,writes the result to the standard output.

输入格式

In the first line of the standard input there is one integer \(k\) (\(1\le k\le 1\ 000\ 000\)) - the length of the string. In the following line a sequence of exactly \(k\) lower-case letters of the English alphabet is written - the string.

输出格式

In the first and only line of the standard output your programme should write an integer - the sum of lengths of maximum periods of all prefixes of the string given in the input.

样例 #1

样例输入 #1

8
babababa

样例输出 #1

24

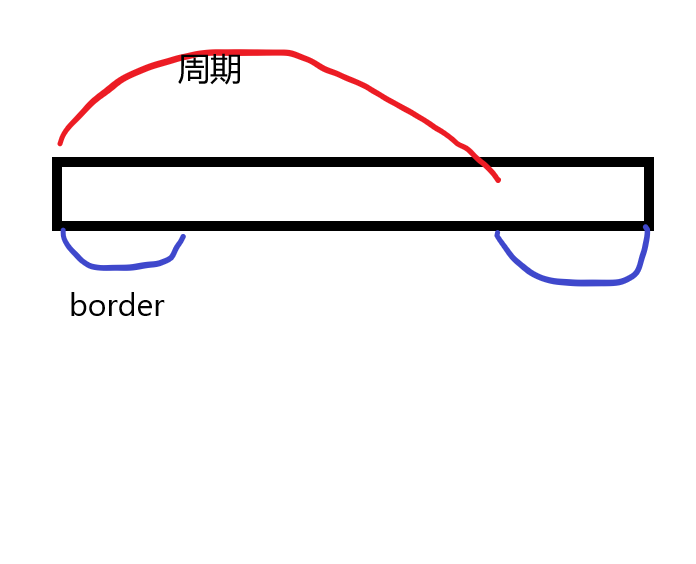
所以我们要用kmp求出前缀函数，然后当前长度减去前缀函数就是周期，求最长周期就是找最小的border
证明:a是Q+Q的前缀并且a的长度<=Q+Q的长度
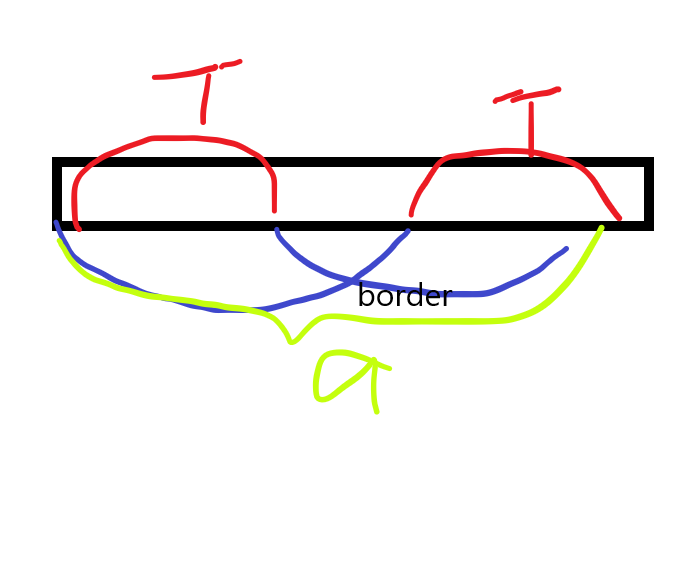
设当前最小前缀函数长度为len,所以周期T=i-len,len<a
如果a>T+T,那么说明前缀函数发生重合,则中间重合部分字符与开头一定相等,则不为最小前缀函数长度，矛盾，所以a是Q+Q的前缀并且a的长度<=Q+Q的长度

点击查看代码

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N = 1e7;
int k,pi[N];
ll ans=0;char s[N];
void kmp()
{
	int j=0;
	for(int i=2;i<=k;i++)
	{
		while(j&&s[i]!=s[j+1])j=pi[j];
		if(s[i]==s[j+1])j++;
		pi[i]=j;
	}
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>k;
	cin>>s+1;
	kmp();
	for(int i=2;i<=k;i++)
	{
		int j=i;
		while(pi[j])j=pi[j];
		if(pi[i])pi[i]=j;
		ans+=i-j;
	}
	cout<<ans;
	return 0;
}