集合计数
集合计数
题目描述
一个有N个元素的集合有2N个不同子集（包含空集），现在要在这2N个集合中取出若干集合（至少一个），使得它们的交集的元素个数为K，求取法的方案数，答案模1000000007。（是质数喔~）
- 输入格式
一行两个整数N,K - 输出格式
一行为答案。 - 样例
- 样例输入
3 2 - 样例输出
6 - 数据范围与提示
- 样例说明
假设原集合为{A,B,C}
则满足条件的方案为：{AB,ABC},{AC,ABC},{BC,ABC},{AB},{AC}, - 数据说明
对于100%的数据，1≤N≤1000000；0≤K≤N；
在这里先说下容斥原理
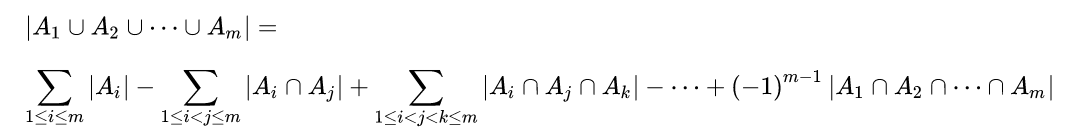
由题可知N个集合有\(2^N\)个子集，
首先我们知道k个元素有\(C^k_n\)种情况,然后,我们考虑在(n-k)个数组成的集合中
且他们互相交集为0的方案数,那么我们就枚举这些集合的交集中比k个元素多x个元素，然后设i=k+x进行计算，则有\(2^{n-i}\)个集合，选或不选就有\(2^{2^{n-i}}\)种情况,但又不包含空集，所以要减1，即为\(2^{2^{n-i}}-1\)，
所以，我们需要遍历i从n-k~0,n-k是总方案,奇数为减,偶数为加
为什么要以这样的顺序
now从2开始
\[F_i=(2^{2^{n-i}}-1)*C_{n-k}^i
\]
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N =1000000,mod=1000000007;
ll n,k;ll f[N+5],ny[N+5],b[N+5];
void init()
{
f[1]=1;
for(int i=2;i<=n;i++)
{
f[i]=f[i-1]*i%mod;
}
ny[0]=ny[1]=1;
for(int i=2;i<=n;i++)
{
ny[i]=(mod-mod/i)*ny[mod%i]%mod;
// cout<<ny[i]<<endl;
}
b[0]=b[1]=1;
for(int i=2;i<=n;i++)
{
b[i]=ny[i]*b[i-1]%mod;
// cout<<b[i]<<endl;
}
}
ll C(int n,int m)
{
if(n<m)return 0;
return f[n]*b[m]%mod*b[n-m]%mod;
}
ll lucas(int n,int m)
{
if(m==0)return 1;
return C(n%mod,m%mod)*lucas(n/mod,m/mod)%mod;
}
ll ans=0;
signed main()
{
scanf("%lld%lld",&n,&k);
init();
ll now=2;int op=1;
for(int i=n-k;i>=0;i--)
{
if(i&1)op=-1;
else op=1;
ans=(ans+op*lucas(n-k,i)*(now-1))%mod;
now=now*now%mod;
// op=-op;
ans=(ans%mod+mod)%mod;
}
ans=ans*C(n,k)%mod;
cout<<ans;
return 0;
}
\[F_i=C_n^i*(2^{2^{n-i}}-1)*C_i^k
\]
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N =1000000,mod=1000000007;
ll n,k;ll f[N+5],ny[N+5],b[N+5];
void init()
{
f[1]=1;
for(int i=2;i<=n;i++)
{
f[i]=f[i-1]*i%mod;
}
ny[0]=ny[1]=1;
for(int i=2;i<=n;i++)
{
ny[i]=(mod-mod/i)*ny[mod%i]%mod;
// cout<<ny[i]<<endl;
}
b[0]=b[1]=1;
for(int i=2;i<=n;i++)
{
b[i]=ny[i]*b[i-1]%mod;
// cout<<b[i]<<endl;
}
}
ll C(int n,int m)
{
if(n<m)return 0;
return f[n]*b[m]%mod*b[n-m]%mod;
}
ll lucas(int n,int m)
{
if(m==0)return 1;
return C(n%mod,m%mod)*lucas(n/mod,m/mod)%mod;
}
ll qpow(ll a,ll b)
{
ll ans=1;
while(b)
{
if(b&1)ans=ans*a%mod;
b>>=1;
a=a*a%mod;
}
return ans;
}
ll ans=0;ll qpw[N+5];
signed main()
{
scanf("%lld%lld",&n,&k);
init();
ll now=2;int op=1;
qpw[1]=2;qpw[0]=1;
for(int i=2;i<=n;i++)
{
qpw[i]=qpw[i-1]*2%(mod-1);
// cout<<qpw[i]<<endl;
}
for(int i=k;i<=n;i++,op=-op)
{
ans=(ans+1ll*lucas(n,i)%mod*(qpow(2,qpw[n-i])-1)%mod*lucas(i,k)%mod*op)%mod;
}
// ans=ans*C(n,k)%mod;
cout<<(ans%mod+mod)%mod;
return 0;
}
为什么\(2^n\)要%(mod-1)啊？
醉翁之意不在酒,我们要计算\(2^{2^{n-i}}-1\)
由
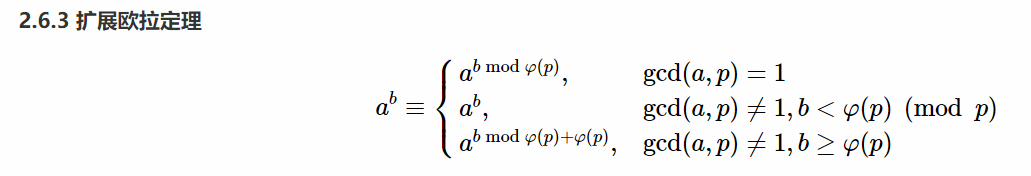
知道\(2^{2^{n-i}}-1\)再%\(p\)
就等同于\(2^{2^{n-i}\%(mod-1)}-1\)
