Tarjan板子
https://csacademy.com/app/graph_editor/
强连通分量（有向边）
常见题
- 建好有向图
找强连通分量，同时记录每个强连通分量中节点的个数
找节点个数最小的强连通分量
点击查看代码
struct Edge
{
int to,next;
}edge[N];
void add(int u,int v)
{
edge[++cnt].to=v;
edge[cnt].next=head[u];
head[u]=cnt;
}
void tarjan(int x)
{
dfn[x]=low[x]=++num;
stk.push(x);
vis[x]=1;
for(int i=head[x];i;i=edge[i].next)
{
if(!dfn[edge[i].to])//ShuBian
{
tarjan(edge[i].to);
low[x]=min(low[x],low[edge[i].to]);
}
else if(vis[edge[i].to])//FanZuBian/HouXiangBian
{
low[x]=min(low[x],dfn[edge[i].to]);
}
}
if(low[x]==dfn[x])
{
int y=0;
t++;
int sum=0;
do
{
y=stk.top();
stk.pop();
vis[y]=0;
belong[y]=t;
sum++;
}while(y!=x);
if(sum!=1)ans=min(ans,sum);
}
}
缩点
- 关于链式前向星缩点的一些事项，有些时候不用存from因为缩点时from就等于i
for(int j=1;j<=n;j++)
{
for(int i=head[j];i;i=edge[i].next)
{
if(belong[edge[i].to]!=belong[edge[i].from])
{
add(belong[edge[i].from],belong[edge[i].to],sum[belong[edge[i].to]],edge2,head2);
}
}
}
统计 出度 如度
for(int j=1;j<=n;j++)
{
for(int i=head[j];i;i=edge[i].next)
{
if(belong[edge[i].to]!=belong[edge[i].from])
{
out[belong[edge[i].from]]++;
in[belong[edge[i].from]]++;
}
}
}
综合应用
Tarjan主要用途是将有环图变为一棵树，然后可能会和SPFA DIJ 拓补排序 DP综合起来
注意拓补排序必须是有向无环图
Trick or Treat on the Farm 采集糖果
求割点+缩点+DP
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N=100005;
int low[N],dfn[N],num,head[N],head2[N],cnt,belong[N],ans=0,sum[N];bool vis[N],cut[N];
stack <int> stk;
int t,n,root;
struct Edge
{
int to,next,from,w;
}edge[N],edge2[N];
void add(int u,int v,int w,Edge *edge,int *head)
{
edge[++cnt].to=v;
edge[cnt].next=head[u];
edge[cnt].from=u;
edge[cnt].w=w;
head[u]=cnt;
}
int f[N]={};bool flag[N];
void dp(int fa)
{
// if(!fa)return;
flag[fa]=true;
// f[fa]=faw;
if(fa)
{
f[fa]+=sum[fa];
}
int faw=f[fa];
for(int i=head2[fa];i;i=edge2[i].next)
{
int son=edge2[i].to;
if(!f[son])dp(son);
f[fa]=max(f[fa],faw+f[son]);
// cout<<son<<" "<<f[son]<<" "<<fa<<' '<<f[fa]<<endl;
}
}
void tarjan(int now)
{
dfn[now]=low[now]=++num;
stk.push(now);
vis[now]=1;
for(int i=head[now];i;i=edge[i].next)
{
int to=edge[i].to;
if(!dfn[to])
{
tarjan(to);
low[now]=min(low[now],low[to]);
}else if(vis[to])
{
low[now]=min(low[now],dfn[to]);
}
}
if(dfn[now]==low[now])
{
t++;
int y;
do
{
y=stk.top();
stk.pop();
vis[y]=0;
sum[t]++;
belong[y]=t;
}while(now!=y);
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int x,y;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>x;
add(i,x,0,edge,head);
}
for(int i=1;i<=n;i++)
{
if(!dfn[i])
{
root=i;
tarjan(i);
}
}
// cout<<t<<endl;
// for(int i=1;i<=n;i++)cout<<belong[i]<<" "<<sum[belong[i]]<<endl;
// cout<<endl;
cnt=0;
for(int i=1;i<=n;i++)
{
for(int j=head[i];j;j=edge[j].next)
{
if(belong[edge[j].from]!=belong[edge[j].to])
{
add(belong[edge[j].from],belong[edge[j].to],sum[belong[edge[j].to]],edge2,head2);
}
}
}
// for(int i=1;i<=t;i++)f[i]=sum[i];
int ans[N]={};
for(int i=1;i<=t;i++)
{
// memset(f,0,sizeof(f));
// f[i]=sum[i];
if(!flag[i])
{
dp(i);
}
}
// cout<<endl;
for(int i=1;i<=n;i++)
{
cout<<f[belong[i]]<<endl;
}
return 0;
}
/*
4
1
3
2
3
*/
无向图上Tarjan算法的应用
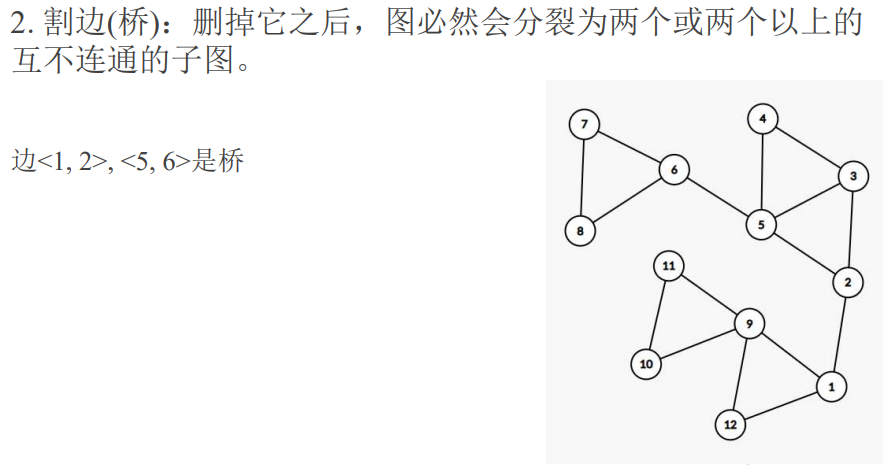
求割点
注意是无向图
点击查看代码
void tarjan(int now)
{
dfn[now]=low[now]=++num;
int son=0;
for(int i=head[now];i;i=edge[i].next)
{
int to=edge[i].to;
if(!dfn[to])
{
son++;
tarjan(to);
low[now]=min(low[now],low[to]);
if(dfn[now]<=low[to])
{
if((now!=root||son>1)&&!cut[now])cut[now]=true,t++;
}
}else
{
low[now]=min(low[now],dfn[to]);
}
}
}
求割边
点击查看代码
void tarjan(int now,int in_edge)
{
dfn[now]=low[now]=++num;
for(int i=head[now];i;i=edge[i].next)
{
int to=edge[i].to;
if(!dfn[to])
{
tarjan(to,i);
low[now]=min(low[now],low[to]);
if(dfn[now]<low[to])
{
ge++;
bridge[i]=bridge[i^1]=true;
}
}else if(i!=(in_edge^1))
{
low[now]=min(low[now],dfn[to]);
}
}
}
Tarjan求双连通分量
法1 DFS缩点
点击查看代码
void tarjan(int now,int in_edge)
{
dfn[now]=low[now]=++num;
for(int i=head[now];i;i=edge[i].next)
{
int to=edge[i].to;
if(!dfn[to])
{
tarjan(to,i);
low[now]=min(low[now],low[to]);
if(dfn[now]<low[to])
{
ge++;
bridge[i]=bridge[i^1]=true;
}
}else if(i!=(in_edge^1))
{
low[now]=min(low[now],dfn[to]);
}
}
}
int c[N]={},dcc;
void dfs(int x)
{
c[x]=dcc;
for(int i=head[x];i;i=edge[i].next)
{
int to=edge[i].to;
if(c[to]||bridge[i])continue;
dfs(to);
}
}
for(int i=1;i<=f;i++)
{
if(!c[i])
{
dcc++;
dfs(i);
}
}
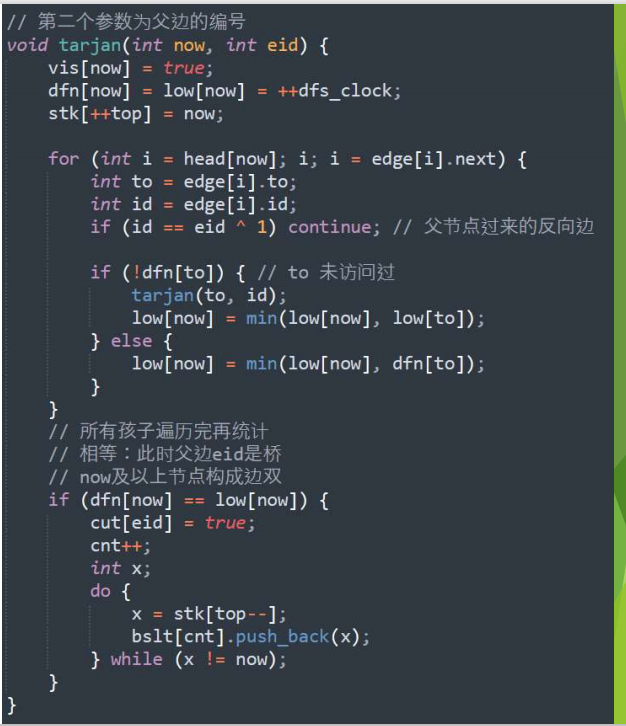
点击查看代码
void tarjan1(int now,int eid)
{
dfn[now]=low[now]=++num;
vis[now]=1;
stk.push(now);
for(int i=head[now];i;i=edge[i].next)
{
int to=edge[i].to;
// int id=edge[i].id;
if(!dfn[to])
{
tarjan1(to,i);
low[now]=min(low[now],low[to]);
}else if(i!=(eid^1))
{
low[now]=min(low[now],dfn[to]);
}
}
if(low[now]==dfn[now])
{
cut[eid]=true;
ge++;
int x;
do
{
x=stk.top();stk.pop();
vis[x]=0;
belong[x]=ge;
}while(x!=now);
}
}
点击查看代码
void tarjan(int now)
{
low[now]=dfn[now]=++num;
stk.push(now);
if(now==root&&!head[now])
{
dcc[++ge].push_back(now);//可以再输入时判断from!=to
return;
}
int son=0;
for(int i=head[now];i;i=edge[i].next)
{
int to=edge[i].to;
if(!dfn[to])
{
tarjan(to);
low[now]=min(low[now],low[to]);
if(dfn[now]<=low[to])
{
son++;
if(now!=root||son>1)cut[now]=true;
ge++;
int x;
do
{
x=stk.top();
stk.pop();
dcc[ge].push_back(x);
}while(x!=to);//注意是x!=to,并不是x!=now
dcc[ge].push_back(now);//割点不一定只在一个人点双中
}
}else
{
low[now]=min(low[now],dfn[to]);
}
}
}
圆方树
与求割点和点双相同
