矩阵乘法

Update2024.7.30

P2044 [NOI2012] 随机数生成器
唐题，但是需要龟速乘法

点击查看代码

#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define ull unsigned long long
#define lid (rt<<1)
#define rid (rt<<1|1)
// #define endl '\n'
//#define int long long
#define pb push_back
#define pii pair<int,int>
using namespace std;
ll g,a,c,x0,n,mod;
ll mul(ll a,ll b)
{
	ll ans=0;
	while(b)
	{
		if(b&1)ans=(ans+a)%mod;
		a=(a+a)%mod;
		b>>=1ll;
	}
	return ans;
}
struct Matrix
{
	ll n,m,a[5][5];
	Matrix(int n,int m):n(n),m(m){memset(a,0,sizeof a);}
	Matrix operator * (const Matrix& A)const
	{
		Matrix ans(2,2);
		for(int i=1;i<=2;i++)
			for(int j=1;j<=2;j++)
				for(int k=1;k<=2;k++)
					ans.a[i][j]=(ans.a[i][j]+mul(a[i][k],A.a[k][j])%mod)%mod;
		return ans;
	}
};
Matrix qpow(Matrix ans,Matrix a,ll b)
{
	while(b)
	{
		if(b&1)ans=a*ans;
		b>>=1ll;
		a=a*a;
	}
	return ans;
}
int main()
{
	speed();
	// freopen("in.in","r",stdin);
	// freopen("out.out","w",stdout);
	Matrix G(2,2);
	Matrix b(2,1);
	cin>>mod>>a>>c>>x0>>n>>g;
	G.a[1][1]=a;G.a[1][2]=c;G.a[2][2]=1;
	b.a[1][1]=x0%mod;
	b.a[2][1]=1;
	// cout<<"*********"<<endl;
	b=qpow(b,G,n);
	cout<<b.a[1][1]%g<<endl;
	return 0;
}

PAST

佳佳的 Fibonacci
由题可知，我们需要用矩阵乘法求出\(T(n)\)
现在就考虑构造几位维的矩阵，我么知道\(F_n=F_{n-1}+F_{n-2}\)
所以求出\(F_n\)至少需要两个元素，然后\(T_n\)呢，就需要\(nF_{n-1}+nF_{n-2}+T_{n-1}\)

\[\left[ \begin{matrix} T_{n-1} & nF_{n-1} & nF_{n-2} & F_{n-1} & F_{n-2} \\ 1 & 0 & 0 & 0 & 0\\ 1 & 1 & 1 & 0 & 0\\ 1 & 1 & 0 & 0 & 0\\ 0 & 1 & 1 & 1 & 1\\ 0 & 1 & 0 & 1 & 0\\ \end{matrix} \right] \]

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=10;
ll mod,n;
inline ll read()
{
	ll x=0,f=1;char ch=getchar();
	for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;
	for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<3)+(x<<1)+(ch^48);
	return x*f;
}
inline void write(ll x){
    if(x<0)putchar('-'),x=-x;
    if(x>9)write(x/10);
    putchar(x%10+48);
}
struct Mat
{
	ll n,m;
	ll a[N][N];
	void zero()
	{
		memset(a,0,sizeof(a));
	}
	void one() { 
		zero();
		for (int i = 1; i <= n; i++) a[i][i] = 1;
	}
	void resize(int x, int y) { 
		n = x; m = y;
	}
	Mat operator *(const Mat &A)const
	{
		Mat res;
		res.resize(n,A.m);
		res.zero();
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=A.m;j++)
			{
				for(int k=1;k<=m;k++)
				{
					res.a[i][j]=((long long)res.a[i][j]+(ll)a[i][k]*A.a[k][j])%mod;
				}		
			}
		}
		return res;
	}
}mat;
Mat qpow(Mat A, ll b) {
	if(b==-1)
	{
		cout<<1;
		exit(0);
	}
	Mat res;
	res.resize(5, 5);
//	res.one();
	res.a[1][1]=3;
    res.a[1][2]=3;
    res.a[1][3]=3;
    res.a[1][4]=1;
    res.a[1][5]=1;
	while (b) {
	if (b & 1) {
	res = res * A;
	}
	A = A * A;
	b >>= 1;
	}
	return res;
}
int main()
{
//	n=read(),mod=read();
	scanf("%d%d",&n,&mod);
//	Mat mat;
	mat.resize(5,5);
	mat.a[1][1]=mat.a[2][1]=mat.a[2][2]=mat.a[2][3]=mat.a[3][1]=mat.a[3][2]=1;
	mat.a[4][4]=mat.a[4][5]=mat.a[5][4]=mat.a[4][2]=mat.a[4][3]=mat.a[5][2]=1;
	mat.a[3][3]=0;
	mat=qpow(mat,n-2);
//	write(mat.a[1][1]);
//	for (int i = 1; i <= 5; i++)cout<<mat.a[i][i]<<" ";
	printf("%lld ",mat.a[1][1]%mod);
	return 0;
}

迷路
\(f_t[i,j]\)表示从i点到j点花费时间为t的方案数
我们假设边权只有1

\[\sum_{k=1}^nf_1[i,k]*f_{t-1}[k,j] \]

f1就是最初的矩阵啊。
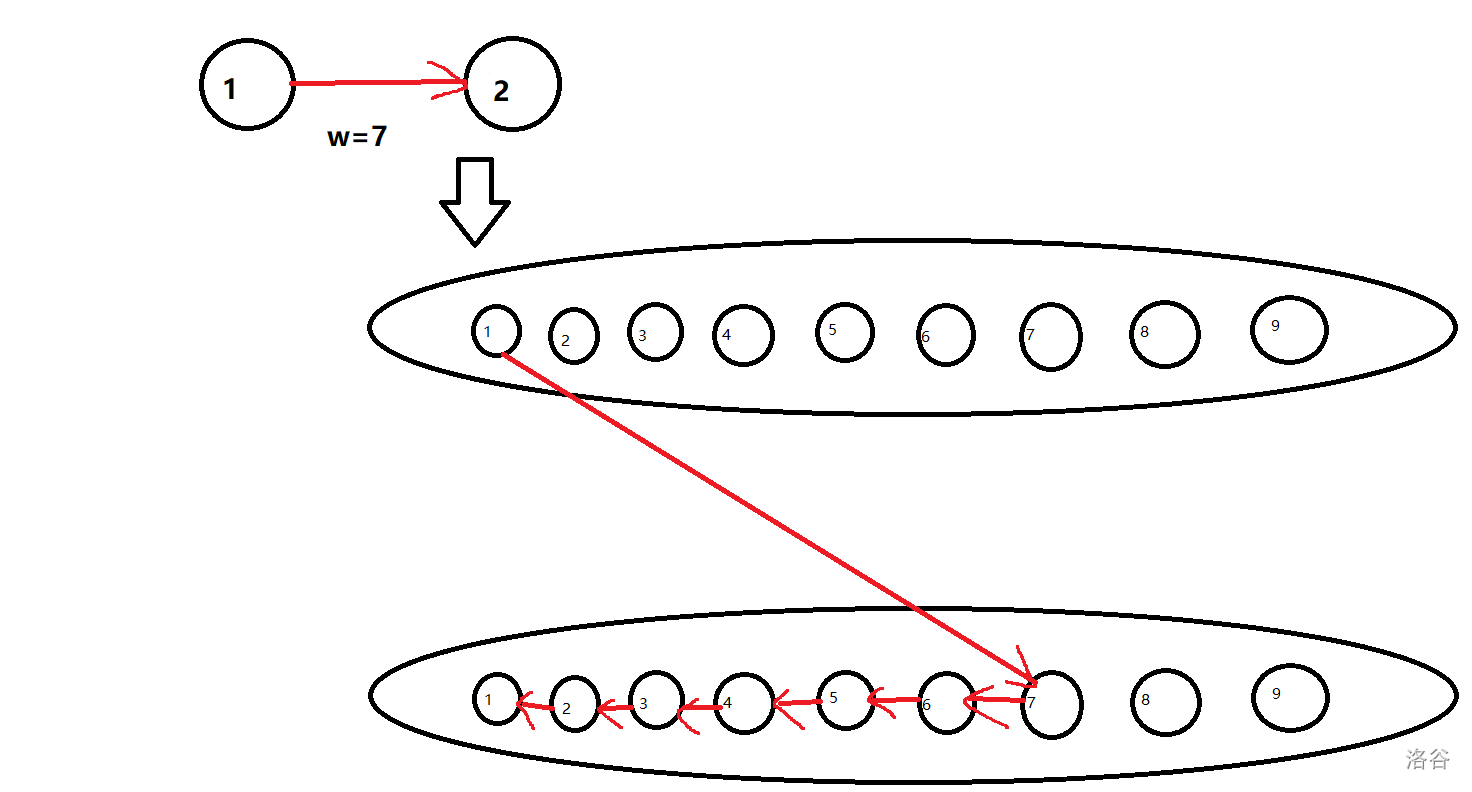
我们1个点建9个小点，只有第1小点可以跨越小点的集合。
那么我们建立第i+1小点到第i小点的w=1的单向边
而要连的两个点1到点2则将小点集合1中的小点1和集合2中的小点w相连。
如下图（只画出了点1到点2经过的路径）

点击查看代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100;
int mod=2009,n,t;
inline int read()
{
	int x=0,f=1;char ch=getchar();
	for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;
	for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<3)+(x<<1)+(ch^48);
	return x*f;
}
inline void write(int x)
{
	if(x<0)putchar('-'),x=-x;
	if(x>9)write(x/10);
	putchar(x%10+48);
}
struct mat
{
	int n,m;
	int a[N][N];
	mat()
	{
		memset(a,0,sizeof(a));
	}
	void clear()
	{
		memset(a,0,sizeof(a));
		for(int i=1;i<=n;i++)a[i][i]=1;
	}
	void resize(int x,int y)
	{
		n=x,m=y;
	}
	mat operator *(const mat &A)const
	{
		mat res;
		res.resize(n,A.n);
//		res.n=A.n;
//		res.c();
//		res.clear();
//		memset(a,0,sizeof(a));
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=A.m;j++)
			{
				for(int k=1;k<=m;k++)
				{
					res.a[i][j]=(res.a[i][j]+(ll)a[i][k]*A.a[k][j])%mod;
				}	
			}		
		}
		return res; 
	}	
};
mat qpow(mat A,int q)
{
	mat res;
	res.resize(9*n,9*n);
//	res.n=A.n;
	res.clear();
	while(q)
	{
		if(q&1)res=res*A;
		A=A*A;
//		q>>=1;
		q/=2;
	}
	return res; 
}

int main()
{
//	n=read(),t=read();
	cin>>n>>t;
	mat rm;
	rm.resize(9*n,9*n);
//	rm.clear();
	int b;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=8;j++)
		{
			rm.a[(i-1)*9+j][(i-1)*9+j+1]=1;
		}
		for(int j=1;j<=n;j++)
		{
			scanf("%1d",&b);
			if(b)
			{
				rm.a[(i-1)*9+b][(j-1)*9+1]=1;
			}
		}
	}
	rm=qpow(rm,t);
	printf("%d",rm.a[1][9*n-8]);
	return 0;
}

点击查看代码

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll mod=2009;
struct Mat
{
	int n,m;
	int a[101][101];
	void zero()
	{
		memset(a,0,sizeof(a));
	}
	void one()
	{
		zero();
		for(int i=1;i<=n;i++)a[i][i]=1;
	}
	void resize(int x,int y)
	{
		n=x;m=y;
	}
	Mat operator *(const Mat &A)const
	{
		Mat res;
		res.resize(n,A.m);
		res.zero();
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=A.m;j++)
			{
				for(int k=1;k<=m;k++)
				{
					res.a[i][j]=(res.a[i][j]+(ll)a[i][k]*A.a[k][j])%mod;
				}
			}
		}
		return res;
	}
	void out()
	{
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=m;j++)
				cout<<a[i][j]<<" ";		
			cout<<endl;
		}

	}
};
ll n;
Mat qpow(Mat A,ll b)
{
	Mat res;
	res.resize(9*n,9*n);
	res.one();
	while(b)
	{
		if(b&1)res=res*A;
		b>>=1;
		A=A*A;
	}
	return res;
}
int pos(int u,int v)
{
	return u+n*v;
}
int main()
{
	int T;
//	ios_base::sync_with_stdio(false);
//	cin.tie(0);cout.tie(0);
	cin>>n>>T;
	Mat res;
	int x;
	res.resize(9*n,9*n);
	res.zero();
	for (int i = 1; i <= n; ++i)
	{
		for (int j = 1; j <= 8; ++j)
			res.a[pos(i, j)][pos(i, j - 1)] = 1; 
		for (int j = 1; j <= n; ++j)
		{
			scanf("%1d", &x); 
			if (x)
 				res.a[i][pos(j, x - 1)] = 1; 
		}
	}
	res=qpow(res,T);
	cout<<res.a[1][n];
	return 0;
}