数论
欧拉定理
\(gcd(a,m)=1,a^{\varphi (m)}=1 \mod m\)
扩展
\[a^b\equiv
\begin{cases}
a^{b\bmod\varphi(p)}, & \gcd(a,p)=1 \\
a^b, & \gcd(a,p)\neq 1,b<\varphi(p)\pmod p \\
a^{b\bmod\varphi(p)+\varphi(p)}, & \gcd(a,p)\neq 1,b\geq\varphi(p)
\end{cases}
\]
求逆元
费马小定理
扩展欧几里得
线性求逆元
4.3.4 小结
求解方程 \(ax\equiv 1\pmod p\) 的方法。
| 方法 | 限定条件 | 时间复杂度 | 备注 |
|---|---|---|---|
| 费马小定理 | 模数为素数 | \(O(\log n)\) | |
| 欧拉定理 | \(a\) 与 \(p\) 互质 | 差不多是 \(O(\sqrt n)\) | |
| 扩展欧几里得 | \(a\) 与 \(p\) 互质 | 据说为 \(O(\ln n)\) | 可以在求解过程中判断是否互质 |
| 线性递推 | 模数为素数 | \(O(n)\) |
中国剩余定理
形如
\[x \equiv a_1 \pmod {n_1}
\]
\[x \equiv a_2 \pmod {n_2}
\]
\[x \equiv a_3 \pmod {n_3}
\]
\[x \equiv a_4 \pmod {n_4}
\]
点击查看代码
LL CRT(int k, LL a[], LL r[]) {
LL n = 1, ans = 0;
for (int i = 1; i <= k; i++) n = n * r[i];
for (int i = 1; i <= k; i++) {
LL m = n / r[i], b, y;
exgcd(m, r[i], b, y); // b * m mod r[i] = 1
ans = (ans + a[i] * m * b % n) % n;
}
return (ans % n + n) % n;
}
扩展中国剩余定理
在某些条件下模数\(n_i\)不一定为质数,这就需要用到扩展中国剩余定理
假设已经求出前k-1个方程组成的同余方程组的一个解为x
且有\(M=\prod_{1到i-1}^{1到k-1}m_i\)这相当于前i-1个m的最大公倍数即为\(M=LCM_{1到i-1}^{1到k-1}m_i\)还更能防止溢出
则k-1个方程的通解为\(x+i*M(i\in Z)\)
则对于第k个方程为\(x+t*M\equiv a_k (mod m)\)
移一下项\(t*M\equiv a_k-x (mod m)\)
然后我们可用扩展欧几里得t
不过根据裴蜀定理
这样的方程存在解的必要条件为\(gcd(a,b)∣c\)
所以无解就输出-1
所以整个算法的思路就是求解k次扩展欧几里得
M∗=bg明显就是令M为前k个m的最小公倍数
- ii即为__int128不想用的话可以用龟速乘
点击查看代码
ii exCRT()
{
ii x,y,k;
ii M=m[1],ans=a[1];//mod num
for(int i=2;i<=n;i++)
{
ii A=M,b=m[i],c=((a[i]-ans)%b+b)%b;
ii gcd=exgcd(A,b,x,y),bg=b/gcd;
if(c%gcd!=0)return -1;
x=x*c/gcd%bg;
ans+=x*M;//更新前k个方程组的答案
M*=bg;//M为前k个m的lcm
ans=(ans%M+M)%M;
}
return (ans%M+M)%M;
}
Lucas定理
求解组合数取模问题,其中模数必须为素数
C(n,m)modp
- 当n很大且n<p可用乘法逆元
- 当n>p公式上的分母可能没有逆元,此时需要Lucas
初始化
void getp()
{
phi[1]=phi[0]=1;
for(int i=2;i<mod;i++)
{
phi[i]=(mod-mod/i)*phi[mod%i]%mod;
}
b[1]=b[0]=1;
for(int i=2;i<mod;i++)
{
b[i]=b[i-1]*phi[i]%mod;
}
jie[1]=jie[0]=1;
for(int i=2;i<mod;i++)
{
jie[i]=jie[i-1]*i%mod;
// cout<<jie[i]<<endl;
}
}
点击查看代码
int C(int n,int m)
{
return n<m?0:jie[n]*b[n-m]*b[m]%mod;
}
int lucas(int n,int m)
{
if(m==0)return 1;
if(m>n-m)
{
m=n-m;
}
return lucas(n/mod,m/mod)*C(n%mod,m%mod)%mod;
}
求解
对于素数p
\[C_{n}^m=C_{[n/p]}^{[m/p]}*C_{[n mod p]}^{[m mod p]}
\]
p的范围不能够太大,一般在\(10^5\)左右
边界条件:当m=0的时候,返回 1
注意 n%p<m%p时,组合数为0
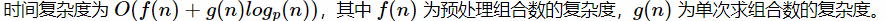
二项式
\[(a+b)^p=\sum_{m=0}^pC_p^ma^mb^{p-m}
\]
对两边取模
\((a+b)^p \equiv a^p+b^p (mod p)\)
扩展卢卡斯定理(exLucas)
当\(p\)不是质数时,需要用到扩展卢卡斯定理求解。
由于模数\(p\)不是质数,由唯一分解定理
\[p=\prod_{i=1}^{r}p_i^{a_i}
\]



