山海经&&Atcoder Alternating String (线段树)
- 前言:为什么把他们放在一起?因为我发现把pushup向上回溯放结构体类型函数里比较方便
并且这两题确实也有相同思想
山海经
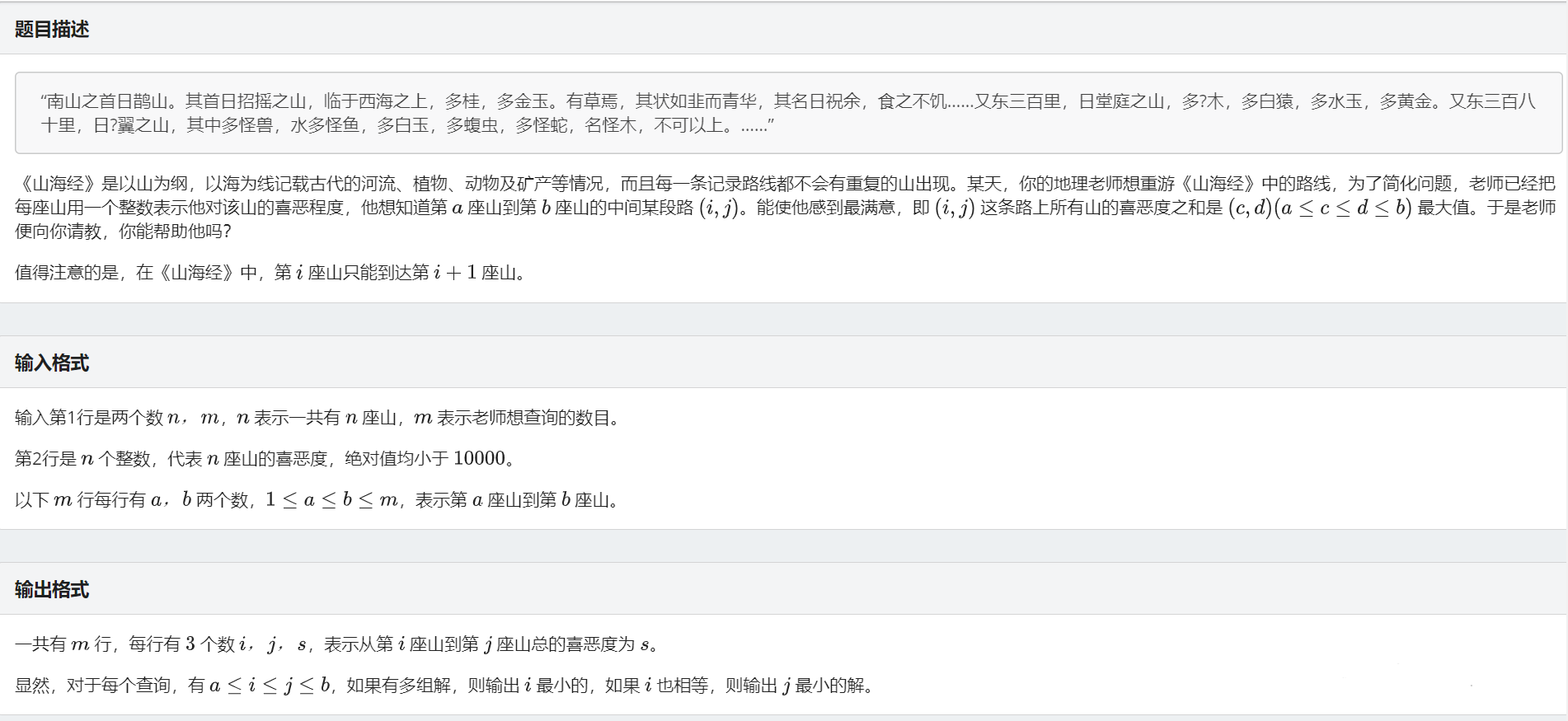
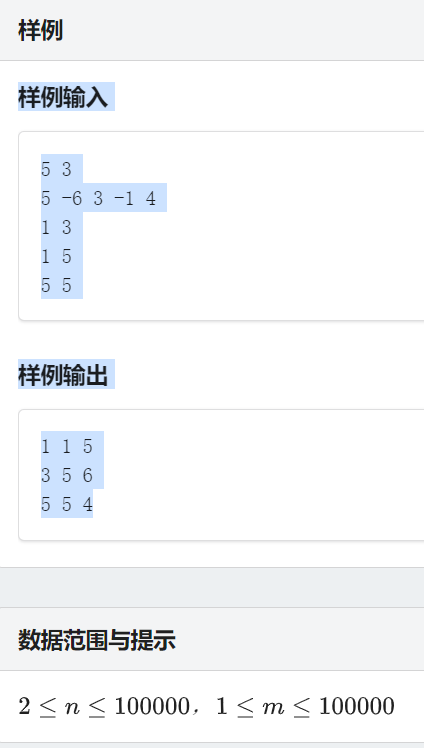
这题分三种情况
- 左子树前缀和+右子树前缀和
2.右子树后缀和 与 右总区间+左子树
3.左区间最大子段 与 右区间最大子段 与 左后缀与右前缀
- 特别要注意的事项
1.LONGLONG
2.是否有等于号(因为要取最小的i,j注意相同情况取最小)
点击查看代码
#include<bits/stdc++.h>
#define lid (rt<<1)
#define rid (rt<<1|1)
using namespace std;
const int N=200010;
int m,n,k,p,a[N];
struct tree
{ int ls=-INT_MAX,rs=-INT_MAX,ms=-INT_MAX;
int l,r,sum;
int ml=-INT_MAX,mr=-INT_MAX;
int ll,rr;
} t[N<<2];
tree push_up(tree x,tree y)
{
tree z;
z.l=x.l;
z.r=y.r;
z.sum=x.sum+y.sum;
if(x.ls<x.sum+y.ls)
{
z.ls=x.sum+y.ls;
z.rr=y.rr;
}
else {z.ls=x.ls;z.rr=x.rr;}
if(y.rs<=y.sum+x.rs)
{
z.rs=y.sum+x.rs;
z.ll=x.ll;
}
else
{
z.rs=y.rs;
z.ll=y.ll;
}
z.ms=x.ms;
z.ml=x.ml;
z.mr=x.mr;
if(x.rs+y.ls>z.ms)
{
z.ms=x.rs+y.ls;
z.ml=x.ll;
z.mr=y.rr;
}
if(z.ms<y.ms)
{
z.ms=y.ms;
z.ml=y.ml;
z.mr=y.mr;
}
return z;
}
void bt(int rt,int l,int r)
{
t[rt].l=l;t[rt].r=r;
if(l==r)
{
t[rt].sum=a[l];
t[rt].ml=t[rt].mr=t[rt].ll=t[rt].rr=l;
t[rt].ls=t[rt].rs=t[rt].ms=a[l];
return;
}
int mid=(t[rt].l+t[rt].r)>>1;
bt(lid,l,mid);
bt(rid,mid+1,r);
t[rt]=push_up(t[lid],t[rid]);
}
tree query(int rt,int l,int r)
{
if(l<=t[rt].l&&t[rt].r<=r)
{
return t[rt];
}
int mid=(t[rt].l+t[rt].r)>>1;
if(r<=mid) return query(lid,l,r);
if(l>mid) return query(rid,l,r);
return push_up(query(lid,l,r),query(rid,l,r));
}
int main()
{
// freopen("hill.in","r",stdin);
// freopen("hill.out","w",stdout);
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++)
scanf("%d",&a[i]);
bt(1,1,n);
// for(int i=1;i<=30;i++)
// {
// cout<<i<<' '<<t[i].l<<' '<<t[i].r <<' '<<t[i].ms<<endl;
// }
for (int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
tree tmp=query(1,x,y);
printf("%d %d %d\n",tmp.ml,tmp.mr,tmp.ms);
}
return 0;
}
Alternating String
这题只需要维护一下左端点值和右端点值即可
用异或和维护
点击查看代码
#include <bits/stdc++.h>
#define lid (rt<<1)
#define rid (rt<<1|1)
using namespace std;
int len,q;
const int N=500000;
int a[N+5];
struct tree
{
int l,r,lz;bool y;
int stw,enw;
}t[N<<2];
tree pushup(tree x,tree y)
{
tree z;
z.l=x.l;z.r=y.r;
z.stw=x.stw;z.enw=y.enw;
if(x.y&&y.y&&x.enw!=y.stw)
{
z.y=1;
}
else z.y=0;
return z;
}
void pushdown(int rt)
{
if(t[rt].lz)
{
int lz=t[rt].lz;
t[rt].lz=0;
t[lid].lz^=lz;
t[rid].lz^=lz;
t[lid].stw^=lz;t[lid].enw^=lz;
t[rid].stw^=lz;t[rid].enw^=lz;
}
}
void bt(int rt,int l,int r)
{
t[rt].l=l;t[rt].r=r;
if(l==r)
{
// t[rt].sum=a[l];
t[rt].y=1;
t[rt].stw=t[rt].enw=a[l];
return;
}
int mid=(l+r)>>1;
bt(lid,l,mid);
bt(rid,mid+1,r);
t[rt]=pushup(t[lid],t[rid]);
}
void update(int rt,int l,int r)
{
if(l<=t[rt].l&&t[rt].r<=r)
{
t[rt].lz^=1;
t[rt].stw^=1;t[rt].enw^=1;
return;
}
pushdown(rt);
int mid=(t[rt].l+t[rt].r)>>1;
if(l<=mid)update(lid,l,r);
if(r>mid)update(rid,l,r);
t[rt]=pushup(t[lid],t[rid]);
}
tree query(int rt,int l,int r)
{
if(l<=t[rt].l&&t[rt].r<=r)
{
return t[rt];
}
pushdown(rt);
int mid=(t[rt].l+t[rt].r)>>1;
int val=0;
if(l<=mid&&r>mid)
{
return pushup(query(lid,l,r),query(rid,l,r));
}
else if(l<=mid)return query(lid,l,r);
else if(r>mid)return query(rid,l,r);
}
int main()
{
scanf("%d%d",&len,&q);
for(int i=1;i<=len;i++)
{
scanf("%1d",&a[i]);
}
int k=1,aa,b;
bt(1,1,len);
for(int i=1;i<=q;i++)
{
scanf("%d%d%d",&k,&aa,&b);
if(k==1)
{
//fanzhuan
update(1,aa,b);
}else
{
if(query(1,aa,b).y)
{
cout<<"Yes"<<endl;
}else
{
cout<<"No"<<endl;
}
}
}
return 0;
}
/*
5 6
10100
2 1 3
2 1 5
1 1 4
2 1 5
1 3 3
2 2 4
*/


