Blocks(单调栈)

题目链接

• 因为可以操作无限次，所以相当于只要一个区间中的所有数相加的平均值大于k即成立
• 首先，我们需要通过前缀和维护，可以在加的时候减去一个k，这样只用判断\(i>j且sum[i]-sum[j]>0\)则在[j+1,i]区间中存在满足题目的连续序列

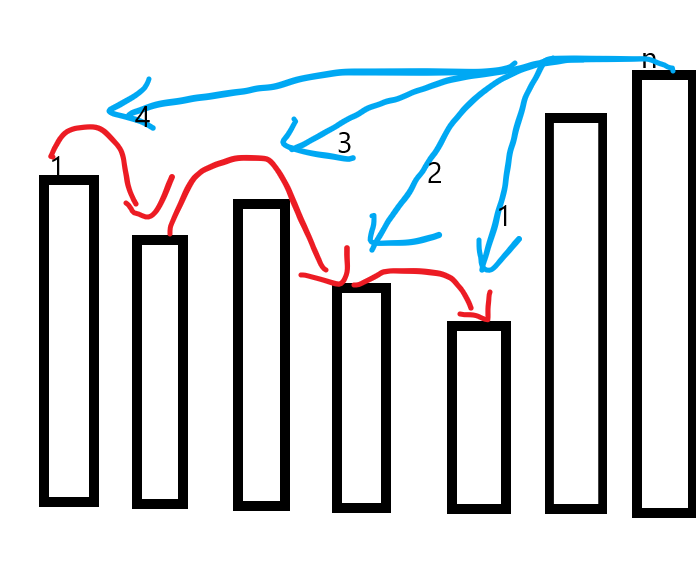
• 如图用红线指的是存入的<0并且单调递减的前缀和sum，以确定左区间，注意，第一个数要存0即top=1时stack[1]=0以便如果出现图中这种情况ans=n-0为最大值;

• 如图蓝线为右n边界与左边界匹配过程，我们要从n开始倒序循环，以求ans做大值

• 需要注意的是，在找左区间及单调递减区间的过程中，如果出现\(sum[i]==sum[j]且i<j\)那么我们取左边的，因为这样与右区间匹配时才尽可能大

  AC代码

  #include <bits/stdc++.h>
  #define int long long
  using namespace std;
  const int N=1000005;
  int n,m,a[N],p,sum[N],stk[N];
  int get(int k)
  {
  //	stack <int> stk;
  	memset(stk,0,sizeof(stk));
  	int top=1;
  	int ans=0;
  	for(int i=1;i<=n;i++)
  	{
  	sum[i]=sum[i-1]+a[i]-k;
  	if(sum[i]<sum[stk[top]])stk[++top]=i;//cout<<i<<endl;
  	}
  	int num=0,len=0,c=0;
  	for(int i=n;i>=1;i--)
  	{
  		while(top&&sum[stk[top]]<=sum[i])
  		{
  			c=stk[top];
  			top--;
  			//stk.pop();
  		}
  		if(sum[c]<=sum[i])ans=max(ans,abs(i-c));
  	}
  	return ans;
  }
  signed main()
  {
  	scanf("%lld%lld",&n,&m);
  	for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
  	int k;
  	for(int i=1;i<=m;i++)
  	{
  		scanf("%lld",&k);
  		memset(sum,0,sizeof(sum));
  		cout<<get(k)<<" ";
  	}
  	return 0;
  }
  /*
  10 5
  10 1 2 4 5 2 6 9 3 1
  5 6 7
  */