树状数组板子
定义
- 树状数组是一个查询和修改复杂度都为log(n)的数据结构。主要用于查
询任意区间的连续元素和,但是每次只能修改一个元素的值;即树状数
组支持的操作:单点修改,区间查询(当区间长度为1时,即单点查询) - 树状数组逻辑上是一棵树,但实际上只是一个数组。
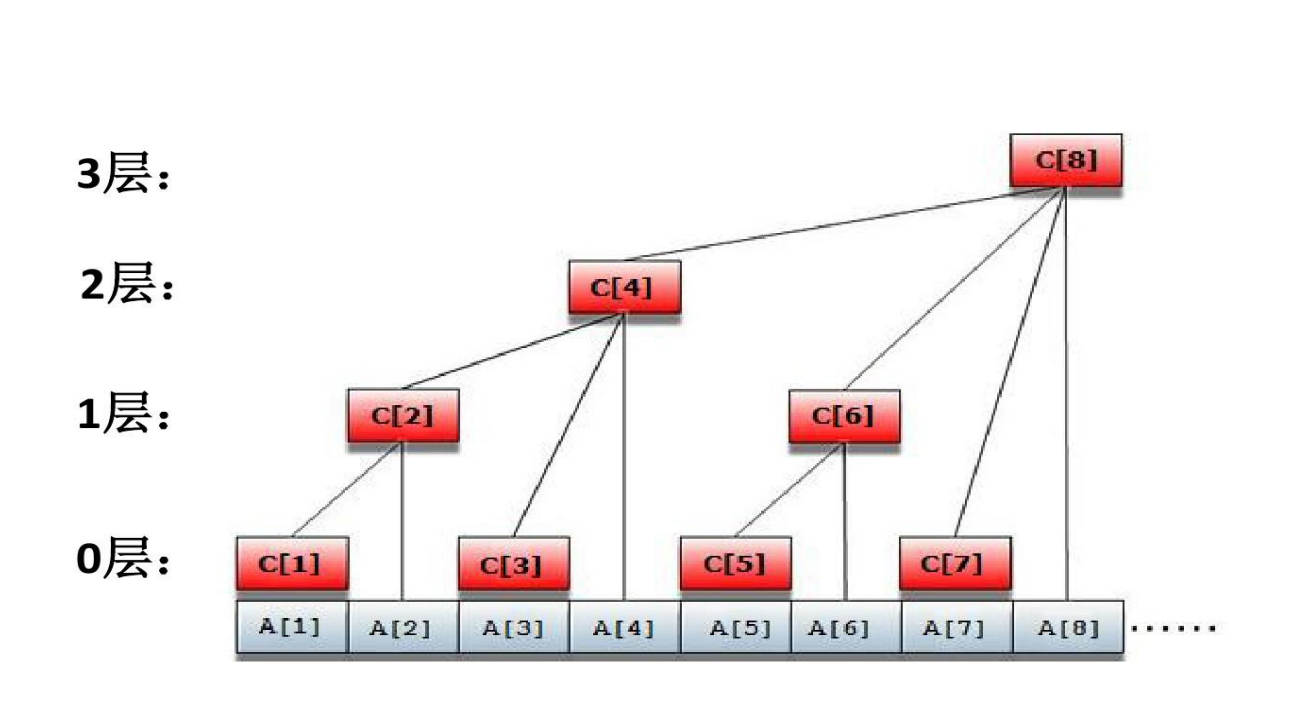
-
设C的某个元素下标为x,则这个结点(前缀和)的管辖区间是2^k个元素(其
中k为x的二进制数的末尾0的个数),且该区间的最后一个元素为Ax
Cx的双亲结点下标y就等于x的二进制数在最后一个1的位置上加1后得到的值。单点修改 区间查询
点击查看代码
#include <bits/stdc++.h> using namespace std; #define int long long int n,A[100005],C[100005]; int lowbit(int x) { return (x&(-x)); } int getsum(int x) { int s=0; while(x) { s+=C[x]; x-=lowbit(x); } return s; } void add(int n,int x,int key) { while(x<=n) { C[x]+=key; x+=lowbit(x); } } signed main() { cin>>n; for(int i=1;i<=n;i++) { cin>>A[i]; add(n,i,A[i]); } int t; cin>>t; string s; int k,p; for(int i=1;i<=t;i++) { cin>>s>>k>>p; if(s=="ADD") { add(n,k,p); }else { printf("%lld\n",getsum(p)-getsum(k-1)); } } return 0; }区间修改 单点查询
点击查看代码
#include <bits/stdc++.h> using namespace std; #define int long long int n,A[100005],C[100005]; inline int lowbit(int x) { return (x&(-x)); } int getsum(int x) { int s=0; while(x) { s+=C[x]; x-=lowbit(x); } return s; } void add(int n,int x,int key) { while(x<=n) { C[x]+=key; x+=lowbit(x); } } signed main() { scanf("%lld",&n); for(int i=1;i<=n;i++) { scanf("%lld",&A[i]); add(n,i,A[i]-A[i-1]); } int m; scanf("%lld",&m); string s; for(int i=1;i<=m;i++) { cin>>s; int a,b,c; if(s=="QUERY") { scanf("%lld",&a); // cout<<"#"; printf("%lld\n",getsum(a)); }else if(s=="ADD") { scanf("%lld%lld%lld",&a,&b,&c); // for(int j=a;j<=b;j++) add(n,a,c); add(n,b+1,-c); } } return 0; }区间修改 区间查询
点击查看代码
#include <bits/stdc++.h> using namespace std; #define int long long int n,A[100005],C[100005],C2[100005]; inline int lowbit(int x) { return (x&(-x)); } int getsum(int x) { int i=x; int s=0; while(x) { s+=(i+1)*C[x]-C2[x]; x-=lowbit(x); } return s; } void add(int n,int x,int key) { int i=x; while(x<=n) { C[x]+=key; C2[x]+=(long long)i*key; x+=lowbit(x); } } signed main() { // if(LONG_LONG_MAX>4611686018427387904)cout<<1; scanf("%lld",&n); for(int i=1;i<=n;i++) { scanf("%lld",&A[i]); add(n,i,A[i]-A[i-1]); } int m; scanf("%lld",&m); string s; for(int i=1;i<=m;i++) { cin>>s; int a,b,c; if(s=="SUM") { scanf("%lld%lld",&a,&b); // cout<<"#"; // int ans=0; // for(int i=a;i<=b;i++)ans+=getsum(i); // printf("%lld\n",ans); printf("%lld\n",getsum(b)-getsum(a-1)); }else if(s=="ADD") { scanf("%lld%lld%lld",&a,&b,&c); // for(int j=a;j<=b;j++) add(n,a,c); add(n,b+1,-c); } } return 0; } -
区间查询即区间内单点查询结果的和
仍然沿用c数组,考虑A数组[1,x]区间和的计算。b[1]被累加了x次,b[2]被
累加了x-1次,...,b[x]被累加了1次。因此得到
∑a[i]=∑{b[i](x-i+1)}=∑{b[i](x+1) - b[i]i}=(x+1)∑b[i]-∑(b[i]i)
所以我们再用树状数组维护一个数组b2[i]=b[i]i,即可完成任务。
用树状数组C1维护b[i]的前缀和,C2维护b2[i]的前缀和。 -
另一种思路:
首先,看更新操作Update(s,t,d)把区间A[s]...A[t]都增加d,我们沿用数组b[i],表示
的意义修改一下,即表示A[i]...A[n]的共同增量,n是数组的大小。那么update操作可
以转化为:
1)令b[s]=b[s]+d,表示将A[s]...A[n]同时增加d,但这样A[t+1]...A[n]就多加了d
2)再令b[t+1]=b[t+1]-d,表示将A[t+1]...A[n]同时减d;
然后来看查询操作Ask(s,t),求A[s]...A[t]的区间和,转化为求前缀和,设
sum[i]= A[1]+...+A[i],则A[s]+...+A[t]=sum[t]-sum[s-1],那么前缀和sum[x]又如何
求呢?它由两部分组成,一是数组的原始和,二是该区间内的累计增量和, 把数组A的
原始值保存在数组org中,并且b[i]对sum[x]的贡献值为b[i](x+1-i),那么
sum[x]=org[1]+...+org[x]+b[1]x+b[2](x-1)+b[3](x-2)+...+b[x]1
=org[1]+...+org[x]+segma(b[i](x+1-i))
=segma(org[i])+(x+1)segma(b[i])-segma(b[i]i),1<=i<=x
这其实就是三个数组org[i], b[i]和b[i]i的前缀和,org[i]的前缀和保持不变,事先
就可以求出来,b[i]和b[i]i的前缀和是不断变化的,可以用两个树状数组来维护。二维树状数组
修改
点击查看代码
void add(int x, int y, int key) { for(int i = x; i <= n; i += lowbit(i)) { for(int j = y; j <= n; j += lowbit(j)) { C[i][j] += key; } }查询
点击查看代码
int getsum(int x,int y) { int ans=0; for(int i=x;i>0;i-=lowbit(i)) { for(int j=y;j>0;j-=lowbit(j)) { ans+=g[i][j]; } } return ans; } -
设二维数组为:
a[][]={ {a11,a12,a13,a14,a15,a16,a17,a18},
{a21,a22,a23,a24,a25,a26,a27,a28},
{a31,a32,a33,a34,a35,a36,a37,a38},
{a41,a42,a43,a44,a45,a46,a47,a48}};
那么C[1][1] = a11,C[1][2] = a11 + a12;
如此当C[1][i]...C[1][j]时跟一维的树状数组是没有什么区别的
那么C[2][1] = a11 + a21,C[2][2] = a11 + a12 + a21 + a21,
如此可以发现
其实C[2][i].....C[2][j],就是C[1][],C[2][],单独的两个一维树
状数组同一位置的值合并在一起
而C[3][1] = a31,C[3][2] = a31 + a32 ......
而C[4][1] = a11 + a21 + a31 + a41,C[4][2] = a11 + a12 +
a21 + a22 + a31 + a32 + a41 + a42
所以二维数组的规律就是,不管是横坐标还是纵坐标,将他们单独
拿出来,他们都符合x += lowbit(x),属于它的父亲节点.

