线段树板子
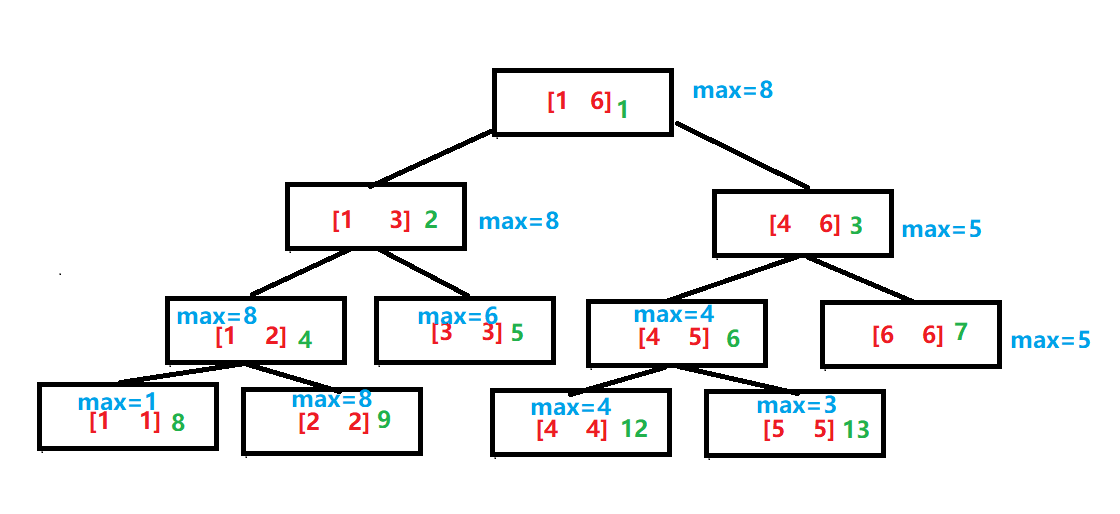
单点修改 区间查询
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <math.h>
#include <string.h>
#include <string>
#include <cstring>
#include <vector>
#include <map>
#include <stack>
#define lid (id << 1)
#define rid (id << 1 | 1)
const int N=100001;
using namespace std;
int a[N],n;
struct tree
{
int l,r,sum,max;
}t[4*N];
void btree(int id,int l,int r)//buildtree
{
t[id].l=l;t[id].r=r;
if(l==r)
{
t[id].sum=a[l];
t[id].max=a[l];
return;
}
int mid=(l+r)>>1;
btree(lid,l,mid);
btree(rid,mid+1,r);
t[id].sum=t[lid].sum+t[rid].sum;
t[id].max=max(t[lid].max,t[rid].max);
}
void modify(int id,int x,int val)//Update
{
if(t[id].l==t[id].r)
{
t[id].sum+=val;t[id].max+=val;
return;
}
int mid=(t[id].l+t[id].r)>>1;
modify(x<=mid?lid:rid,x,val);
t[id].sum=t[lid].sum+t[rid].sum;
t[id].max=max(t[lid].max,t[rid].max);
}
int query(int id,int l,int r)
{
if(t[id].l>=l&&t[id].r<=r)return t[id].sum;
int mid=(t[id].l+t[id].r)>>1;
if(r<=mid)return query(lid,l,r);
if(l>mid)return query(rid,l,r);
return query(lid,l,mid)+query(rid,mid+1,r);
}
int main()
{
cin>>n;
string s;
for(int i=1;i<=n;i++)
{
cin>>a[i];
// modify(1,i,a[i]);
}
int m;
cin>>m;
if(n==0)return 0;
btree(1,1,n);
for(int i=1;i<=m;i++)
{
cin>>s;
if(s[0]=='S')
{
int s,t;
cin>>s>>t;
cout<<query(1,s,t)<<endl;
}
else
{
int k,d;
cin>>k>>d;
modify(1,k,d);
}
}
return 0;
}
区间修改 单点查询
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <math.h>
#include <string.h>
#include <string>
#include <cstring>
#include <vector>
#include <map>
#include <stack>
#define lid (rt << 1)
#define rid (rt << 1 | 1)
#define int long long
const int N=100001;
using namespace std;
int a[N],n;
struct tree
{
int l,r,sum,max,lz;
}t[N<<2];
void bt(int rt,int l,int r)
{
t[rt].l=l;t[rt].r=r;
if(t[rt].l==t[rt].r)
{
t[rt].sum=a[l];
t[rt].max=a[l];
return;
}
int mid=(t[rt].l+t[rt].r)>>1;
bt(lid,l,mid);
bt(rid,mid+1,r);
t[rt].sum=t[lid].sum+t[rid].sum;
t[rt].max=max(t[lid].max,t[rid].max);
}
void pushdown(int rt)
{
if(t[rt].lz)//´Ë½ÚµãÓÐÑÓ³Ù±ê¼Ç
{
int lz=t[rt].lz;
t[rt].lz=0;
t[lid].lz+=lz;
t[rid].lz+=lz;
t[lid].sum+=lz*(t[lid].r-t[lid].l+1);
t[rid].sum+=lz*(t[rid].r-t[rid].l+1);
}
}
//int ask(int rt,int a, int b,int l,int r)//Çø¼äºÍ²éѯ
//{
// if(l>b||r<a) return 0;
// if(a>=l&&b<=r) return t[rt].sum;
// int mid=(a+b)>>1;
// pushdown(rt);
// return ask(lid, a, mid, l, r) + ask(rid, mid + 1, b, l, r);
//}
int query(int rt,int l,int r)
{
if(t[rt].l>=l&&t[rt].r<=r)return t[rt].sum;
pushdown(rt);
int mid=(t[rt].l+t[rt].r)>>1;
int val=0;
if(l<=mid)val+=query(lid,l,r);
if(r>mid)val+=query(rid,l,r);
return val;
}
void pushup(int rt)
{
t[rt].sum=t[lid].sum+t[rid].sum;
t[rt].max=max(t[lid].max,t[rid].max);
}
void update(int rt,int l,int r,int k)
{
if(t[rt].l>=l&&t[rt].r<=r)
{
t[rt].sum+=k*(t[rt].r-t[rt].l+1);
t[rt].lz+=k;
return;
}
pushdown(rt);
int mid=(t[rt].l+t[rt].r)>>1;
if(l<=mid)update(lid,l,r,k);
if(r>mid)update(rid,l,r,k);
pushup(rt);
}
signed main()
{
cin>>n;
string s;
for(int i=1;i<=n;i++)
{
cin>>a[i];
// modify(1,i,a[i]);
}
int m;
cin>>m;
// if(n==0)return 0;
bt(1,1,n);
for(int i=1;i<=m;i++)
{
cin>>s;
if(s[0]=='Q')
{
int s,t;
cin>>s;
cout<<query(1,s,s)<<endl;//如果是查询区间则改掉这里
}
else
{
int k,d,c;
cin>>k>>d>>c;
update(1,k,d,c);
}
}
return 0;
}
区间修改 区间查询
点击查看代码
同上
分步
记得开LONGLONG
#define lid (rt << 1)
#define rid (rt << 1 | 1)
#define int long long
const int N=100001;
int a[N],n;
struct tree
{
int l,r,sum,max,lz;
}t[N<<2];
建树
点击查看代码
void bt(int rt,int l,int r)
{
t[rt].l=l;t[rt].r=r;
if(t[rt].l==t[rt].r)
{
t[rt].sum=a[l];
t[rt].max=a[l];
return;
}
int mid=(t[rt].l+t[rt].r)>>1;
bt(lid,l,mid);
bt(rid,mid+1,r);
t[rt].sum=t[lid].sum+t[rid].sum;
t[rt].max=max(t[lid].max,t[rid].max);
}
延迟标记
点击查看代码
void pushdown(int rt)
{
if(t[rt].lz)
{
int lz=t[rt].lz;
t[rt].lz=0;
t[lid].lz+=lz;
t[rid].lz+=lz;
t[lid].sum+=lz*(t[lid].r-t[lid].l+1); //注意,如果是区间修改,单点查询最大值，正确答案为t[lid].sum+=lz;
t[rid].sum+=lz*(t[rid].r-t[rid].l+1); //注意,如果是区间修改,单点查询最大值，正确答案为t[rid].sum+=lz;
}
}
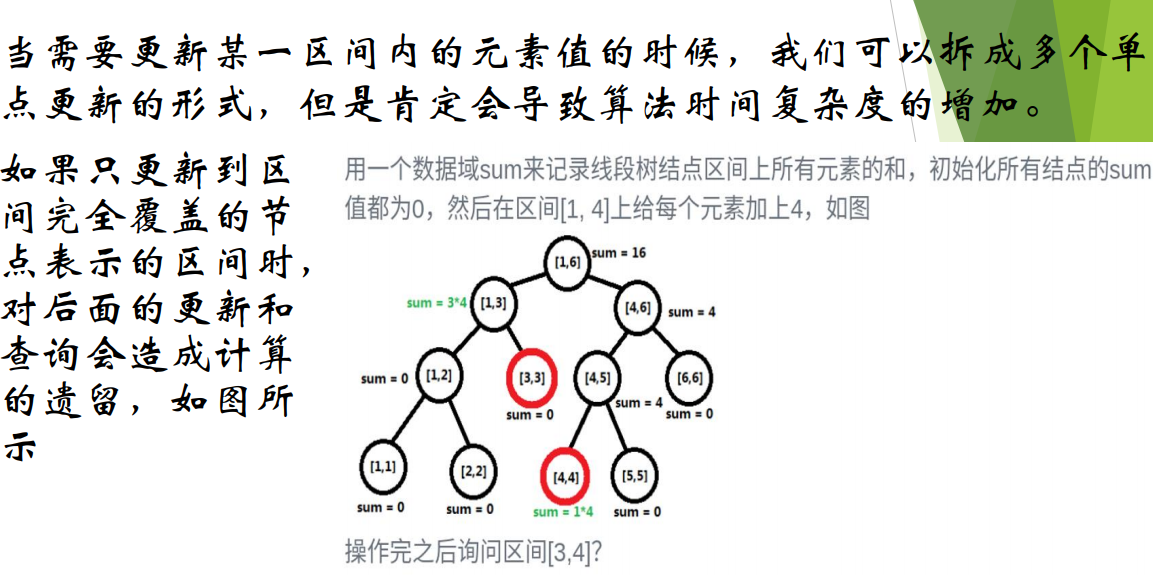
- 1>做区间更新时，如果要更新的区间能够完全覆盖
当前节点表示的区间，则在此节点上做个标记
（表示此节点曾被修改，但子节点尚未被更新），
不再继续向下更新，同时在回溯时更新父节点的
信息。
2>如果在之后的维护或查询过程中需要对这个节点
的某个儿子递归地进行处理，则将这个标记分解，
传递给它的两个儿子节点。
3>这种在需要的时候才进行分解的做法，使我们整
体的时间复杂度仍在O(log2N) 的水平上
回溯
点击查看代码
void pushup(int rt)
{
t[rt].sum=t[lid].sum+t[rid].sum;
t[rt].max=max(t[lid].max,t[rid].max);
}
区间更新
点击查看代码
void update(int rt,int l,int r,int k)
{
if(t[rt].l>=l&&t[rt].r<=r)
{
t[rt].sum+=k*(t[rt].r-t[rt].l+1);
t[rt].lz+=k;
return;
}
pushdown(rt);
int mid=(t[rt].l+t[rt].r)>>1;
if(l<=mid)update(lid,l,r,k);
if(r>mid)update(rid,l,r,k);
//pushup(rt);
t[rt].sum=t[lid].sum+t[rid].sum;
t[rt].max=max(t[lid].max,t[rid].max);
}
区间更新，区间查询(单点查询l==r)
点击查看代码
int query(int rt,int l,int r)
{
if(t[rt].l>=l&&t[rt].r<=r)return t[rt].sum;
pushdown(rt);
int mid=(t[rt].l+t[rt].r)>>1;
int val=0;
if(l<=mid)val+=query(lid,l,r);
if(r>mid)val+=query(rid,l,r);
return val;
}
单点更新
点击查看代码
void modify(int id,int x,int val)//Update
{
if(t[id].l==t[id].r)
{
t[id].sum+=val;t[id].max+=val;//注意是更新到还是增加了
return;
}
int mid=(t[id].l+t[id].r)>>1;
modify(x<=mid?lid:rid,x,val);
t[id].sum=t[lid].sum+t[rid].sum;
t[id].max=max(t[lid].max,t[rid].max);
}
单点更新 单点查询
点击查看代码
int query(int id,int l,int r)
{
if(t[id].l>=l&&t[id].r<=r)return t[id].sum;
int mid=(t[id].l+t[id].r)>>1;
if(r<=mid)return query(lid,l,r);
if(l>mid)return query(rid,l,r);
return query(lid,l,r)+query(rid,l,r);
}
区间修改 单点查询
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n,A[100005],C[100005];
inline int lowbit(int x)
{
return (x&(-x));
}
int getsum(int x)
{
int s=0;
while(x)
{
s+=C[x];
x-=lowbit(x);
}
return s;
}
void add(int n,int x,int key)
{
while(x<=n)
{
C[x]+=key;
x+=lowbit(x);
}
}
signed main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&A[i]);
add(n,i,A[i]-A[i-1]);
}
int m;
scanf("%lld",&m);
string s;
for(int i=1;i<=m;i++)
{
cin>>s;
int a,b,c;
if(s=="QUERY")
{
scanf("%lld",&a);
// cout<<"#";
printf("%lld\n",getsum(a));
}else if(s=="ADD")
{
scanf("%lld%lld%lld",&a,&b,&c);
// for(int j=a;j<=b;j++)
add(n,a,c);
add(n,b+1,-c);
}
}
return 0;
}
