DP总结
DP总结
背包DP
-0/1背包
-完全背包
-多重背包
-分组背包
-依赖背包
-二维背包
-树形背包DP
0/1背包
朴素版
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
//f[i][j]表示前i个物品,体积不超过j时的最大价值
//不选第i个物品时,f[i][j] = f[i-1][j]
//选第i个物品时,f[i][j] = f[i-1][j-v[i]]+w[i],保证j>=v[i]
int f[maxn][maxn] = {}; //默认全为0,这样后面就不需要再初始化
int n = 0, m = 0; //n件物品,m为背包总容量
int v[maxn] = {}, w[maxn] = {}; //v表示第i件物品体积,w为第i件物品价值
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i=1; i<=n; i++)
{
for(int j=0; j<=m; j++)
{
f[i][j] = f[i-1][j];
if(j>=v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
}
}
printf("%d", f[n][m]);
return 0;
}
滚动数组版
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
int f[2][maxn] = {}; //默认全为0,这样后面就不需要再初始化
int n = 0, m = 0; //n件物品,m为背包总容量
int v[maxn] = {}, w[maxn] = {}; //v表示第i件物品体积,w为第i件物品价值
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i=1; i<=n; i++)
{
for(int j=0; j<=m; j++)
{
f[i&1][j] = f[(i-1)&1][j];
if(j>=v[i]) f[i&1][j] = max(f[i&1][j], f[(i-1)&1][j-v[i]] + w[i]);
}
}
printf("%d", f[n&1][m]);
return 0;
一维
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
int f[maxn] = {}; //默认全为0,这样后面就不需要再初始化
int n = 0, m = 0; //n件物品,m为背包总容量
int v[maxn] = {}, w[maxn] = {}; //v表示第i件物品体积,w为第i件物品价值
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i=1; i<=n; i++)
{
for(int j=m; j>=v[i]; j--)
{
f[j] = max(f[j], f[j-v[i]] + w[i]);
}
}
printf("%d", f[m]);
return 0;
}
完全背包

朴素版
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
//f[i][j]表示前i个物品,体积不超过j时的最大价值
//f[i][j]=max(f[i-1][j], f[i-1][j], f[i-1][j-v[i]]+w[i], f[i-1][j-2*v[i]]+2*w[i], ....)
int f[maxn][maxn] = {}; //默认全为0,这样后面就不需要再初始化
int n = 0, m = 0; //n件物品,m为背包总容量
int v[maxn] = {}, w[maxn] = {}; //v表示第i件物品体积,w为第i件物品价值
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i=1; i<=n; i++)
{
for(int j=0; j<=m; j++)
{
for(int k=0; k*v[i]<=j; k++)
{
f[i][j] = max(f[i][j], f[i-1][j-k*v[i]] + k*w[i]);
}
}
}
printf("%d", f[n][m]);
return 0;
}
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
//f[i][j]表示前i个物品,体积不超过j时的最大价值
//f[i][j] = max(f[i-1][j], f[i][j-v] + w)
int f[maxn][maxn] = {}; //默认全为0,这样后面就不需要再初始化
int n = 0, m = 0; //n件物品,m为背包总容量
int v[maxn] = {}, w[maxn] = {}; //v表示第i件物品体积,w为第i件物品价值
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i=1; i<=n; i++)
{
for(int j=0; j<=m; j++)
{
f[i][j] = f[i-1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j-v[i]] + w[i]);
}
}
printf("%d", f[n][m]);
return 0;
}
一维
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
int f[maxn] = {}; //默认全为0,这样后面就不需要再初始化
int n = 0, m = 0; //n件物品,m为背包总容量
int v[maxn] = {}, w[maxn] = {}; //v表示第i件物品体积,w为第i件物品价值
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i=1; i<=n; i++)
{
for(int j=v[i]; j<=m; j++)
{
f[j] = max(f[j], f[j-v[i]] + w[i]);
}
}
printf("%d", f[m]);
return 0;
}
多重背包
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 110;
int n = 0, m = 0;
int f[maxn] = {};
int v[maxn] = {}, w[maxn] = {}, s[maxn] = {};
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &v[i], &w[i], &s[i]);
}
for(int i=1; i<=n; i++)
{
for(int j=1; j<=s[i]; j++)
{
for(int k=m; k>=v[i]; k--)
{
f[k] = max(f[k], f[k-v[i]] + w[i]);
}
}
}
printf("%d", f[m]);
return 0;
}
二进制拆分多重背包
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 15000;
const int maxm = 2010;
int n = 0, m = 0;
int f[maxm] = {};
int v[maxn] = {}, w[maxn] = {}, s[maxn] = {}, cnt = 0;
int main()
{
int vi = 0, wi = 0, si = 0;
scanf("%d%d", &n, &m);
//二进制拆分
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &vi, &wi, &si);
if(si > m / vi) si = m / vi;
for(int j=1; j<=si; j<<=1)
{
v[++cnt] = j * vi;
w[cnt] = j * wi;
si -= j;
}
if(si > 0)
{
v[++cnt] = si * vi;
w[cnt] = si * wi;
}
}
//0/1背包
for(int i=1; i<=cnt; i++)
{
for(int j=m; j>=v[i]; j--)
{
f[j] = max(f[j], f[j-v[i]] + w[i]);
}
}
printf("%d", f[m]);
return 0;
}
分组背包
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 40;
const int maxm = 210;
//分组背包
int n = 0, m = 0, t = 0;
int v[maxn] = {}, c[maxn] = {};
//g[i][j]表示第i组第j个物品的编号
int g[15][maxn] = {};
//f[i][j]表示前i组物品,体积不超过j的最大价值
int f[15][maxm] = {};
int main()
{
int x = 0;
scanf("%d%d%d", &m, &n, &t);
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &v[i], &c[i], &x);
g[x][++g[x][0]] = i;
}
for(int i=1; i<=t; i++)
{
for(int j=0; j<=m; j++)
{
f[i][j] = f[i-1][j];
for(int k=1; k<=g[i][0]; k++)
{
if(j >= v[g[i][k]])
{
x = g[i][k];
f[i][j] = max(f[i][j], f[i-1][j-v[x]] + c[x]);
}
}
}
}
printf("%d", f[t][m]);
return 0;
}
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 40;
const int maxm = 210;
//分组背包
int n = 0, m = 0, t = 0;
int v[maxn] = {}, c[maxn] = {}, g[15][maxn] = {};
int f[maxm] = {};
int main()
{
int x = 0;
scanf("%d%d%d", &m, &n, &t);
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &v[i], &c[i], &x);
g[x][++g[x][0]] = i;
}
for(int i=1; i<=t; i++)
{
for(int j=m; j>=0; j--)
{
for(int k=1; k<=g[i][0]; k++)
{
if(j >= v[g[i][k]])
{
x = g[i][k];
f[j] = max(f[j], f[j-v[x]] + c[x]);
}
}
}
}
printf("%d", f[m]);
return 0;
}
vector数组存最方便,也可用链式前向行
依赖背包 例题Consumer
点击查看代码
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n,w;
int dp[100005];
int num[55];// 记录每组物品个数
int priceOfBox[55];// 盒子价格
int price[55][15];// 物品花费
int value[55][15];// 物品价值
int dp_tmp[100005]; // 临时数组
int main()
{
while(scanf("%d%d",&n,&w) != EOF) {
memset(dp,0,sizeof(dp));
for(int i = 1;i <= n;i++) {
scanf("%d",&priceOfBox[i]);
scanf("%d",&num[i]);
for(int j = 1;j <= num[i];j++) {
scanf("%d%d",&price[i][j],&value[i][j]);
}
}
for(int i = 1;i <= n;i++) {
memcpy(dp_tmp,dp,sizeof(dp));
// 买不起盒子,打好标记
for(int j = 0;j < priceOfBox[i];j++)
dp[j] = -1;
for(int j = priceOfBox[i];j <= w;j++)
dp[j] = dp_tmp[j-priceOfBox[i]];
for(int j = 1;j <= num[i];j++) {
for(int k = w;k >= price[i][j];k--) {
if(dp[k-price[i][j]] != -1)
dp[k] = max(dp[k],dp[k-price[i][j]] + value[i][j]);
}
}
for(int j = 0;j <= w;j++)
dp[j] = max(dp_tmp[j],dp[j]);
}
printf("%d\n",dp[w]);
}
return 0;
}
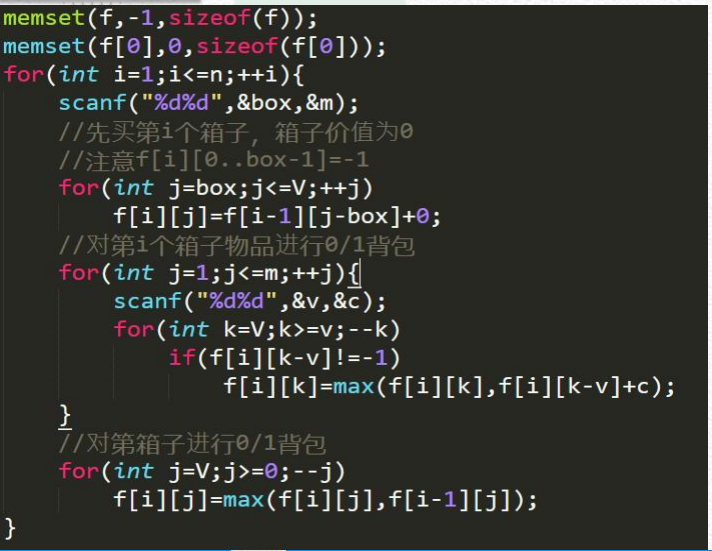
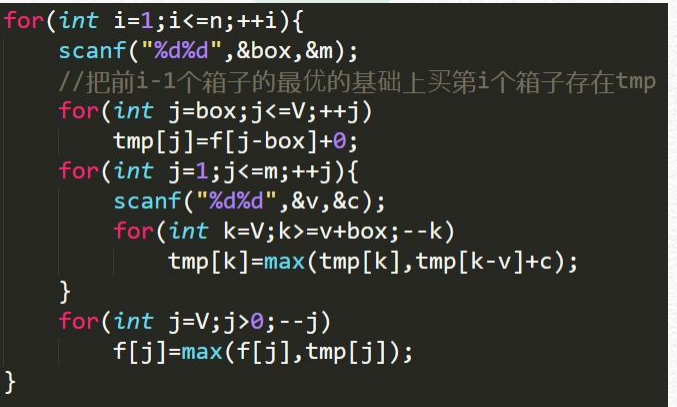
二维费用背包
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 60;
const int maxm = 410;
//二维费用背包
int n = 0, v = 0, m = 0;
int a[maxn] = {}, b[maxn] = {}, c[maxn] = {};
int f[maxm][maxm] = {};
int main()
{
scanf("%d%d%d", &v, &m, &n);
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &a[i], &b[i], &c[i]);
}
for(int i=1; i<=n; i++)
{
for(int j=v; j>=a[i]; j--)
{
for(int k=m; k>=b[i]; k--)
{
f[j][k] = max(f[j][k], f[j-a[i]][k-b[i]] + c[i]);
}
}
}
printf("%d", f[v][m]);
return 0;
}
树形背包DP
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int m,n,w[1005],f[1005][1005];
vector <int> a[1005];
void dp(int fa)
{
for(int i=0;i<a[fa].size();i++)
{
int son=a[fa][i];
dp(son);
for(int j=n;j>=0;j--)
for(int k=0;k<=j;k++)
f[fa][j]=max(f[fa][j],f[fa][j-k]+f[son][k]);
}
if(fa)
{
for(int j=n;j>0;j--)
f[fa][j]=f[fa][j-1]+w[fa];
}
}
int main()
{
cin>>m>>n;
int x,y;
for(int i=1;i<=m;i++)
{
cin>>x>>w[i];
a[x].push_back(i);
}
dp(0);
cout<<f[0][n];
return 0;
}
Vector
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int m,n,w[1005],f[1005][1005];
vector <int> a[1005];
void dp(int fa)
{
for(int i=0;i<a[fa].size();i++)
{
int son=a[fa][i];
dp(son);
for(int j=n;j>=0;j--)
for(int k=0;k<j;k++)
f[fa][j]=max(f[fa][j],f[fa][j-k-1]+f[son][k]+w[son]);
}
}
int main()
{
cin>>m>>n;
int x,y;
for(int i=1;i<=m;i++)
{
cin>>x>>w[i];
a[x].push_back(i);//x->i
}
dp(0);
cout<<f[0][n];
return 0;
}
链式前向星
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,cnt;
int f[200][200];
struct node{
int from;
int to;
int w;
}edge[20000];
int head[2000];
void dfs(int zi,int gen){
for(int i=head[zi];i;i=edge[i].from){
int to=edge[i].to;
dfs(to,zi);
for(int j=m;j>=1;j--){
for(int k=0;k<j;k++){
f[zi][j]=max(f[zi][j],f[edge[i].to][k]+f[zi][j-k-1]+edge[i].w);
}
}
}
}
void add(int from,int to,int w){
cnt++;
edge[cnt].from=head[from];
edge[cnt].to=to;
edge[cnt].w=w;
head[from]=cnt;
}
int main(){
int from,to,w;
cin>>n>>m;
for(int i=1;i<=n-1;i++){
cin>>from>>to>>w;
add(from,to,w);
}
dfs(1,0);
cout<<f[1][m];
}
oi-wiki树形背包DP 树形DP
点击查看代码
#include <algorithm>
#include <cstdio>
#include <vector>
using namespace std;
int f[305][305], s[305], n, m;
vector<int> e[305];
int dfs(int u) {
int p = 1;
f[u][1] = s[u];
for (auto v : e[u]) {
int siz = dfs(v);
// 注意下面两重循环的上界和下界
// 只考虑已经合并过的子树,以及选的课程数超过 m+1 的状态没有意义
for (int i = min(p, m + 1); i; i--)
for (int j = 1; j <= siz && i + j <= m + 1; j++)
f[u][i + j] = max(f[u][i + j], f[u][i] + f[v][j]); // 转移方程
p += siz;//p表示的是节点数
}
return p;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
int k;
scanf("%d%d", &k, &s[i]);
e[k].push_back(i);
}
dfs(0);
printf("%d", f[0][m + 1]);
return 0;
}
注意事项:dfs中循环,第一层倒序n/m->1(到0或1没影响)!!!注意第二层如果以零为起点,那么(应为要预留出一个空间给根节点所以j+1-1)k<=j,如果以1为起点或其他则看k<=j-1,还有如果最后没有初始化,而是写在了dfs的两层循环中,(以1为根为例)即dp[fa][j]=max(dp[fa][j],dp[fa][j-根的体积-k]+f[son][k]+父亲的权值)额外注意vector存图父亲的权值指向的是儿子还是自身
小结:注意背包DP特征如体积.价值.空间(给定一个限制值求另外一个值的最优)
还有初始化的问题max0x3f,min-0x3f,可行性-1
f[0]=0之类的,还有至多同一个dp[i][j]=max(dp[i][j],dp[i-1][j-v]+w)
至少一个初始化成级小dp[i][j]=max(dp[i][j],dp[i-1][j-v]+w,dp[i][j-v]+w)
线性DP
点击查看代码
for(int i=1;i<=n;i++)
{
for(int j=1;j<i;j++)
{
if(a[j]<a[i])
{
f[i]=max(f[i],f[j]+1);
}
}
ans=max(ans,f[i]);//注意,如果放for循环里面如果i=1时最大会被忽略,所以,如果想放里面,可以改为就j<=i
}
特征:线性 成一定规律(如递增递减)
导弹拦截问题简单版
- 偏序集
n 偏序是在集合X上的二元关系≤(这只是个抽象符号,不
是“小于或等于”),它满足自反性、反对称性和传递性。
即,对于X中的任意元素a,b和c,有:
–自反性:a≤a;
–反对称性:如果a≤b且b≤a,则有a=b;
–传递性:如果a≤b且b≤c,则a≤c 。
带有偏序关系的集合称为偏序集。
令(X,≤)是一个偏序集,对于集合中的两个元素a、b,如
果有a≤b或者b≤a,则称a和b是可比的,否则a和b不可比。
一个反链A是X的一个子集,它的任意两个元素都不能进
行比较。
一个链C是X的一个子集,它的任意两个元素都可比
-定理
在X中,对于元素a,如果任意元素b,都有a≤b,则称a为极小元。
定理1:令(X,≤)是一个有限偏序集,并令r是其最大链的大小。则X
可以被划分成r个但不能再少的反链。
其对偶定理称为Dilworth定理:
令(X,≤)是一个有限偏序集,并令m是反链的最大的大小。则X可以
被划分成m个但不能再少的链。
拦截导弹 要求最少的覆盖,按照Dilworth定理:最少链划分= 最长反链长
最长公共子串问题
定义:字串是一个字符串中连续的一段,公共子串即为几个字符串都含有的子串.
\(\ dp[i][j]=\begin{cases}dp[i-1][j-1]+1(s[x]==s[y])\\0 (s[x]!=s[y])\end{cases}\)
最长公共子序列问题
定义:字序列是一个字符串中有序的一段,即序列中的每个数在原序列内都从左到右排列,公共子序列即为几个字符串都含有的子序列.
\(\ dp[i][j]=\begin{cases}dp[i-1][j-1]+1(s[x]==s[y])\\max(dp[i][j-1],dp[i-1][j]) (s[x]!=s[y])\end{cases}\)
点击查看代码
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= n; j ++ )
{
f[i][j] = f[i - 1][j];
if (a[i] == b[j])
{
int maxv = 1;
for (int k = 1; k < j; k ++ )
if (a[i] > b[k])
maxv = max(maxv, f[i - 1][k] + 1);
f[i][j] = max(f[i][j], maxv);
}
}
}
区间DP
特征:一个区间,如字符串
点击查看代码
for (len = 2; len <= n; len++)
for (i = 1; i <= 2 * n - 1 - len; i++) {
int j = len + i - 1;
for (k = i; k < j; k++)
f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j]) + sum[j] - sum[i - 1];//以石子合并为例
}
石子合并优化


点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 4010;
int n = 0;
//f[i][j]表示i~j堆这个区间的总分最多
//1、f[i][j]由f[i+1][j]与a[i]合并而来
//2、f[i][j]由f[i][j-1]与a[j]合并而来
int f[maxn][maxn] = {};
//s表示a的前缀和
int a[maxn] = {}, s[maxn] = {};
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
a[n+i] = a[i];
}
for(int i=1; i<=n*2; i++) s[i] = s[i-1] + a[i];
for(int len=2; len<=n; len++) //阶段,区间长度
{
for(int i=1; i<=2*n-len+1; i++)
{
int j = i + len - 1;
f[i][j] = max(f[i+1][j], f[i][j-1]) + s[j] - s[i-1];
}
}
int ans = 0;
for(int i=1; i<=n; i++)
{
ans = max(ans, f[i][n+i-1]);
}
printf("%d\n", ans);
return 0;
}
坐标DP
特征:形如其名,一个图上的DP,有时需要自己构建图
树形DP
特征:一般关系成树形,二叉树,森林树,如何构建树
如森林树转二叉树就是第一个作为左儿子,第二个右儿子,第三个作为右儿子的右儿子,类推

