博客作业04--树

1.学习总结

1.1树结构思维导图

1.2 树结构学习体会

• 1.学树结构觉得有点吃力了，因为有很多的内容，很零碎，还不能很好的联会贯通
• 2.难点重要点很多，二叉树，哈夫曼树等等
• 3.很多函数需要使用递归，很容易想不通掉进去
• 4.一些基本性质很重要，在写程序的时候有时用到会简化很多
• 5.知道了要写好伪代码，读懂伪代码的重要性

2.PTA实验作业

2.1 题目1：6-4 jmu-ds-表达式树

2.2 设计思路（伪代码或流程图）

 建二叉表达式树
void InitExpTree(BTree &T,string str) {     
建op栈,op.push('#')
初始化根节点栈：stacktree栈
while(表达式未结束)
{     
     if(ch==操作数)  
                生成一个只有根节点的子树T。stacktree.push(T)   
    if(ch==运算符)
    {       
           while(ch<op栈顶运算符)  栈顶优先级高，则                    
             {        创建一个树结点T，数据为op.top()
                     stacktree弹出2个根节点T1，T2
                     T->lchild=T1,  T->rchild=T2
                    stacktree.push(T);               
                }
          if(ch>op栈顶运算符)  
                       op.push(ch)   
          if(ch==op栈顶运算符)  则 op.pop() 。只有(和)优先级相等
    }
}
while(op.top()!='#')
{
创建一个树结点T，数据为op.top()
 s弹出2个根节点T1，T2
T->lchild=T1,  T->rchild=T2
s.push(T); 
}
T=s.top();

计算表达式树 
double EvaluateExTree(BTree T)
{
递归出口 T为空
返回 data
a=递归调用左孩子
b=递归调用右孩子
判断符号
返回a符号b
}

2.3 代码截图

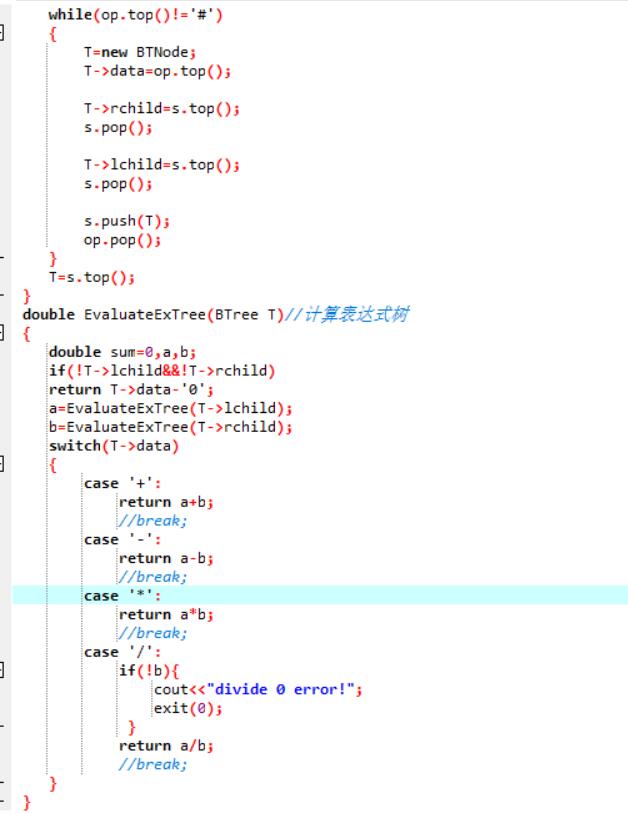
2.4 PTA提交列表说明

括号计算还没有想到怎么算，继续调试。

2.1 题目2：7-8 jmu-ds-二叉树叶子结点带权路径长度和

2.2 设计思路（伪代码或流程图）

用递归法将二叉树的顺序存储结构转换成链式存储结构
trans（）
递归出口 i大于数组长度或者i小于0
if（内容为#）表示该节点为空
else
创建根节点
递归创建左子树
递归创建右子树
返回根节点

找叶子节点并求WPL
leaves(BTree BT,int h)
if（节点不为空）{
 该节点的左右孩子为空 sum=sum+(BT->data-'0')*h; sum为全局变量
 递归判断左子树，并使高度加一
 递归判断右子树，并使高度加一
}

2.3 代码截图

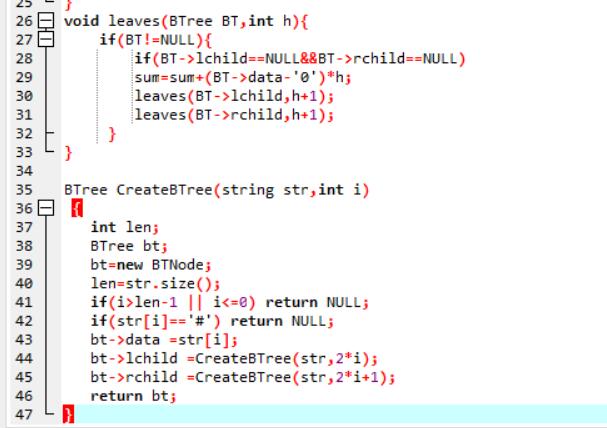
2.4 PTA提交列表说明

这个题一开始是用队列创建树，并没有找到合适的方法。求解WPL是想在寻找叶子节点的同时调用高度函数，但一直停止工作。

2.1 题目3：7-7 修理牧场

2.2 设计思路（伪代码或流程图）

构造哈夫曼树
CreateHT(HTNode ht[],int n)
{
n个叶子节点，哈夫曼树共有2n-1个节点
1.初始化哈夫曼数组ht，包含2n-1个节点
所有2n-1个节点的parent、lchild和rchild域置为初值-1。
输入n个叶子节点有data和weight域值
2.构造非叶子节点ht[i]（存放在ht[n]～ht[2n-2]中）
从ht[0] ～ht[i-1]中找出根节点（即其parent域为-1）最小的两个节点ht[lnode]和ht[rnode]
ht[lnode]和ht[rnode]的双亲节点置为ht[i]，并且ht[i].weight= ht[lnode].weight+ht[rnode].weight。
3.如此这样直到所有2n-1个非叶子节点处理完毕。
}

寻找非叶子节点
void notLeaves(HTNode ht[],int n)
{
遍历整个ht数组
if（左右孩子节点不为-1）
则累加节点的权重
}

2.3 代码截图

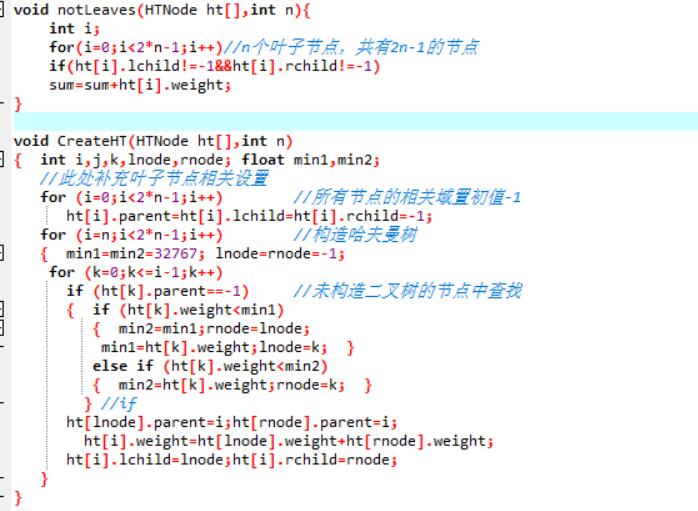
2.4 PTA提交列表说明

后面的两个测试点之前一直过不了，更换了求钱数的方法。

3.截图本周题目集的PTA最后排名

3.1 PTA排名

3.2 我的得分：195

4. 阅读代码

• 题目：求二叉树的宽度

#include<iostream>
#include<queue>
#include<string>
#include<math.h> 
using namespace std;
typedef struct node{
	char data;
	struct node *lchild;
	struct node *rchild;
}BTNode;
typedef BTNode *BTree;
BTree CreateBTree(string str,int i);
int wide(BTree BT,string str);
int fun(BTree b);
void levelnumber(BTree b,int h,int a[]);
int main(){
	int i=1,w;
	BTree BT;
	string a;
	cin>>a;
	BT=CreateBTree(a,i);
	w=fun(BT);
	cout<<w;
	return 0;
}
BTree CreateBTree(string str,int i)
 {
   int len;
   BTree bt;
   bt=new BTNode;
   len=str.size();
   if(i>len-1 || i<=0) return NULL;
   if(str[i]=='#') return NULL;
   bt->data =str[i];
   bt->lchild =CreateBTree(str,2*i); 
   bt->rchild =CreateBTree(str,2*i+1); 	
   return bt;
}
void levelnumber(BTree b,int h,int a[])
{
 if (b==NULL)   return;
 else
  {
	a[h]++;
	levelnumber(b->lchild,h+1,a);
	levelnumber(b->rchild,h+1,a);
  }
}
int fun(BTree b)
{     
    int width=0,i;   
    int a[20];
  for (i=1;i<20;i++)   a[i]=0;		//a设置所有元素初始化为0
  levelnumber(b,1,a);
  i=1;
  while (a[i]!=0)	
  {      
        if (a[i]>width)   width=a[i];
	 i++;
  }
      return width;
 }

这是上机考试求宽度的题，当时没有全对。去看了之前课堂派上的代码，看了看，改了改。
优点：它在求每层的宽度的时候使用了递归代码，操作简单。

5. 代码Git提交记录截图