1、遗传算法是非常好的非线性搜索算法,是一种全局寻优的近似方法
2、遗传算法的步骤:
1)将问题的解写成编码的形式,随机产生第一代种群。
2)选择:选择一些染色体来产生下一代。根据适应度F(i)以比例选择算法从种群中选出2个个体。
3)对选出的2个个体按交叉概率执行交叉操作,再按变异概率执行变异操作
4)重插入:将处理后的2个个体加入新的种群。
3、工具箱
这里运用的工具箱是GATBX遗传算法工具箱
1)创建随机的初始种群
Chrom=crtbp(Nind, Lind)
Nind种群个体数目,Lind是个体编码的长度;Chrom是Nind*Lind的矩阵
2)选择
适应度值Fitnv=rank(Objv)
根据目标函数值分配适应度值,注意该函数是从最小值方向分配的。
Selch=select('method', chrom, Fitnv, GGap)
method:选择的方法,sus(遍历随机抽样)/rws(轮盘赌)
GGAp:代沟,衡量每一代被选择发生变化的程度
3)交叉
Selch=recombin('method', oldchrom, XoVR)
method:交叉的方法,xovsp(单点交叉)/ xovdp(两点交叉)/ xovsh(洗牌交叉)
XoVR:交叉概率
4)变异
Selch=mut(oldchrom)
一般用mut完成二进制和整数的变异操作
5)重插入
[Chrom ObjV]=reins(Chrom, SelCh, Subpop, Insopt, ObjVch, ObjVSel)
Subpop:指明Chorm中子种群的个数
Insopt:指明子代代替父代的方法,0代表均匀随机选择,1代表适应度选择
4、举例(此处将不断更新)
example1:
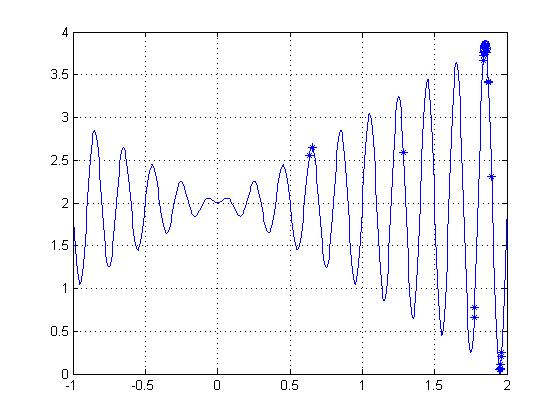
简单一元函数优化实例,利用遗传算法计算下面函数的最大值:
f(x)=xsin(10pi*x)+2 -1=<x<=2
选择二进制编码,种群中个体数目为40,每个种群的长度为20,使用代沟为0.9,最大遗传代数为25
译码矩阵结构:FieldD=[len; lb; ub; code; scale; lbin; ubin]
译码矩阵说明:
len – 包含在Chrom中的每个子串的长度,注意sum(len)=length(Chrom);
lb、ub – 行向量,分别指明每个变量使用的上界和下界;
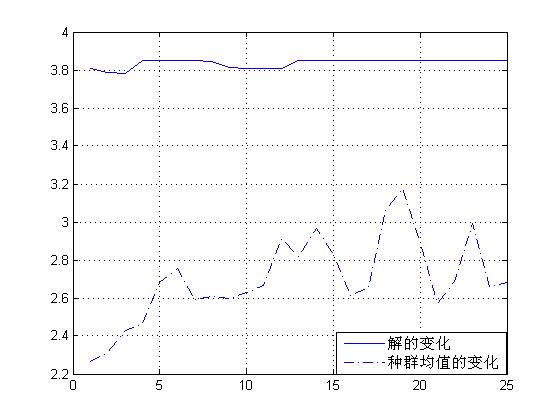
code – 二进制行向量,指明子串是怎样编码的,code(i)=1为标准二进制编码,code(i)=0则为格雷编码;
scale – 二进制行向量,指明每个子串是否使用对数或算术刻度,scale(i)=0为算术刻度,scale(i)=1则为对数刻度;
lbin、ubin – 二进制行向量,指明表示范围中是否包含每个边界,选择lbin=0或ubin=0,表示从范围中去掉边界;lbin=1或ubin=1则表示范围中包含边界;
Solution
1 figure(1); 2 fplot('variable.*sin(10*pi*variable)+2.0',[-1,2]); %画出函数曲线 3 %定义遗传算法参数 4 NIND=40; %个体数目(Number of individuals) 5 MAXGEN=25; %最大遗传代数(Maximum number of generations) 6 PRECI=20; %变量的二进制位数(Precision of variables) 7 GGAP=0.9; %代沟(Generation gap) 8 trace=zeros(2, MAXGEN); %寻优结果的初始值 9 FieldD=[20;-1;2;1;0;1;1]; %区域描述器(Build field descriptor) 10 Chrom=crtbp(NIND, PRECI); %初始种群 11 gen=0; %代计数器 12 variable=bs2rv(Chrom, FieldD); %计算初始种群的十进制转换 13 ObjV=variable.*sin(10*pi*variable)+2.0; %计算目标函数值 14 while gen<MAXGEN 15 FitnV=ranking(-ObjV); %分配适应度值(Assign fitness values) 16 SelCh=select('sus', Chrom, FitnV, GGAP); %选择 17 SelCh=recombin('xovsp', SelCh, 0.7); %重组 18 SelCh=mut(SelCh); %变异 19 variable=bs2rv(SelCh, FieldD); %子代个体的十进制转换 20 ObjVSel=variable.*sin(10*pi*variable)+2.0; %计算子代的目标函数值 21 [Chrom ObjV]=reins(Chrom, SelCh, 1, 1, ObjV, ObjVSel); %重插入子代的新种群 22 variable=bs2rv(Chrom, FieldD); 23 gen=gen+1; %代计数器增加 24 %输出最优解及其序号,并在目标函数图像中标出,Y为最优解,I为种群的序号 25 [Y, I]=max(ObjV);hold on; 26 plot(variable(I), Y, 'bo'); 27 trace(1, gen)=max(ObjV); %遗传算法性能跟踪 28 trace(2, gen)=sum(ObjV)/length(ObjV); 29 end 30 variable=bs2rv(Chrom, FieldD); %最优个体的十进制转换 31 hold on, grid; 32 plot(variable,ObjV,'b*'); 33 figure(2); 34 plot(trace(1,:)); 35 hold on; 36 plot(trace(2,:),'-.');grid 37 legend('解的变化','种群均值的变化')