图最短路径之Dijkstra
算法的简介:
1)该算法用来计算最短距离,但不计算路径信息。我们可以创建一个父数组,在距离更新时更新父数组如[prim的实现,并使用它来显示从源到不同顶点的最短路径。 2)代码用于无向图,相同的Dijkstra函数也可以用于有向图。 3) 代码查找从源到所有顶点的最短距离。如果我们只对从源到单个目标的最短距离感兴趣,我们可以在选取的最小距离顶点等于目标时中断for循环(算法的步骤3.a)。 4) 实现的时间复杂度为 O(V^2)。如果输入,则可以借助二进制堆将其简化为 O(E log V)。 5)Dijkstra的算法不适用于具有负权重周期的图形。对于具有负边的图形,可以使用Floyd或者Bellman-Ford算法。
算法的过程
给定图形和图形中的源顶点,查找从源到给定图形中所有顶点的最短路径。 Dijkstra的算法与[Prim的最小生成树算法]非常相似。与Prim的MST一样,我们生成一个SPT(最短路径树),以给定的源作为根。我们维护两个集合,一个集合包含最短路径树中包含的顶点,另一个集合包含尚未包含在最短路径树中的顶点。在算法的每一步中,我们都会找到一个位于另一个集合(尚未包含的集合)中的顶点,并且与源的距离最小。
算法 1) 创建一个集合 sptSet(最短路径树集),用于跟踪最短路径树中包含的顶点,即计算并最终确定其与源的最小距离。最初,此集为空。 2) 为输入图中的所有顶点分配距离值。将所有距离值初始化为 INFINITE。为源顶点指定距离值为 0,以便首先选取它。 3) 虽然 sptSet 不包括所有顶点 ....a) 选择一个在 sptSet 中不存在且具有最小距离值的顶点 u。 ....b) 将您包括在 sptSet 中。 ....c) 更新您所有相邻顶点的距离值。要更新距离值,请循环访问所有相邻顶点。对于每个相邻顶点 v,如果 u 的距离值(来自源)和边 u-v 的权重之和小于 v 的距离值,则更新 v 的距离值。
让我们通过以下示例来理解:
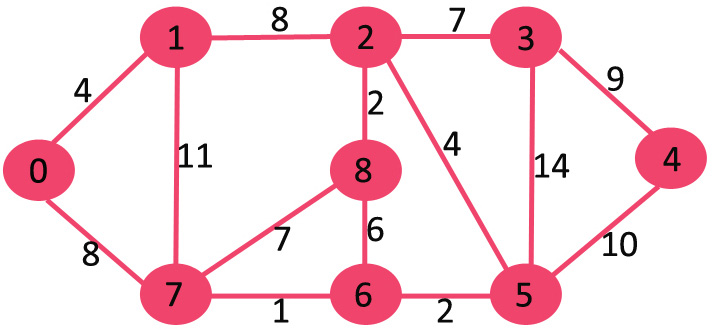
设置的 sptSet 最初是空的,分配给顶点的距离是 {0, INF, INF, INF, INF, INF, INF} ,其中 INF 表示无限。现在选取具有最小距离值的顶点。选取顶点 0,将其包含在 sptSet 中。所以sptSet变得{0}。在 sptSet 中包含 0 后,更新其相邻顶点的距离值。相邻顶点 0 为 1 和 7。距离值 1 和 7 将更新为 4 和 8。以下子图显示顶点及其距离值,仅显示具有有限距离值的顶点。SPT 中包含的顶点以绿色显示。
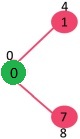
选取具有最小距离值且尚未包含在 SPT(不在 sptSET 中)的顶点。选取顶点 1 并将其添加到 sptSet 中。所以 sptSet 现在变成 {0, 1}。更新相邻顶点 1 的距离值。顶点 2 的距离值变为 12。
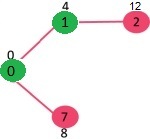
选取具有最小距离值且尚未包含在 SPT(不在 sptSET 中)的顶点。选取顶点 7。所以 sptSet 现在变成 {0, 1, 7}。更新相邻顶点的距离值 7。顶点 6 和 8 的距离值变为有限(分别为 15 和 9)。
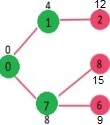
选取具有最小距离值且尚未包含在 SPT(不在 sptSET 中)的顶点。选取顶点 6。所以 sptSet 现在变成 {0, 1, 7, 6}。更新相邻顶点 6 的距离值。将更新顶点 5 和 8 的距离值。
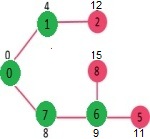
我们重复上述步骤,直到 sptSet 包含给定图形的所有顶点。最后,我们得到以下最短路径树(SPT)。

我们使用布尔数组 sptSet[] 来表示 SPT 中包含的顶点集。如果值 sptSet[v] 为真,则顶点 v 包含在 SPT 中,否则不包含。数组 dist[] 用于存储所有顶点的最短距离值。
算法的实现
golang
// F 代表两点之间不可达
const F = 10000
func dijkstra(graph [][]int, source int) []int {
n := len(graph)
if source >= n {
return []int{}
}
dist := make([]int, n)
visited := make([]bool, n)
for i := 0; i < n; i++ {
dist[i] = graph[source][i]
visited[i] = false
}
dist[source] = 0
visited[source] = true
for i := 1; i < n; i++ {
temMinDis := F
curIdx := -1
for j := 0; j < n; j++ {
if !visited[j] && dist[j] < temMinDis {
temMinDis = dist[j]
curIdx = j
}
}
visited[curIdx] = true
dist[curIdx] = temMinDis
for k := 0; k < n; k++ {
if !visited[k] && dist[curIdx]+graph[curIdx][k] < dist[k] {
dist[k] = dist[curIdx] + graph[curIdx][k]
}
}
}
return dist
}
Java
package graph.dijkstra;
import java.util.Arrays;
public class ShortestPathOfDijkstra {
private static final int MAX = 10000;
/**
* 接受一个有向图的权重矩阵,和一个起点编号start(从0编号,顶点存在数组中)
*
* @param graph graph
* @param startPointIndex startPointIndex
* @return 返回一个int[] 数组,表示从start到它的最短路径长度
*/
public static int[] dijsktra(int[][] graph, int startPointIndex) {
int length = graph.length;
//标记当前该顶点的最短路径是否已经求出,true表示已经求出
boolean[] visited = new boolean[length];
//start点的最短距离已经求出
for (int i = 0; i < graph.length; i++) {//初始化s集合,只有起始点
if (i == startPointIndex) {
visited[i] = true;
} else {
visited[i] = false;
}
}
//存放从start到各个点的最短距离
int[] shortDistance = new int[length];
for (int i = 0; i < graph.length; i++) {//初始化,起始点到其他点的距离。
shortDistance[i] = graph[startPointIndex][i];
}
//start到他本身的距离最短为0
shortDistance[startPointIndex] = 0;
//存放从start点到各点的最短路径的字符串表示
String[] path = new String[length];
for (int i = 0; i < length; i++) {
path[i] = startPointIndex + "->" + i;
}
for (int count = 1; count < length; count++) {
int k = -1;
int dmin = MAX;
for (int i = 0; i < length; i++) {
if (!visited[i] && shortDistance[i] < dmin) {
dmin = shortDistance[i];
k = i;
}
}
//选出一个距离start最近的未标记的顶点 将新选出的顶点标记为以求出最短路径,且到start的最短路径为dmin。
shortDistance[k] = dmin;
visited[k] = true;