红黑树详细讲解(结合JavaTreeMap)
1:红黑树简介
红黑树又称红-黑二叉树,它首先是一颗二叉树,它具体二叉树所有的特性。同时红黑树更是一颗自平衡的排序二叉树。根据二叉查找树的概念可以得出正常情况下查找的时间复杂度为O(log n),但是可能会出现一种极端的情况使得这颗二叉树变为线性的则查找的时间复杂度直接降到(O(n)),为了避免这种情况红黑树应运而生,红黑树是一颗自平衡的二叉树,是解决二叉查找树变为线性结构的一种实现方式。
1.1:红黑树概念:
1、每个节点都只能是红色或者黑色
2、根节点是黑色
3、每个叶节点(NIL节点,空节点)是黑色的。
4、如果一个结点是红的,则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这棵树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。所以红黑树它是复杂而高效的,其检索效率O(log n)。
1.2:红黑树自平衡的关键操作
1:左旋转(如下图:图片来源网络)
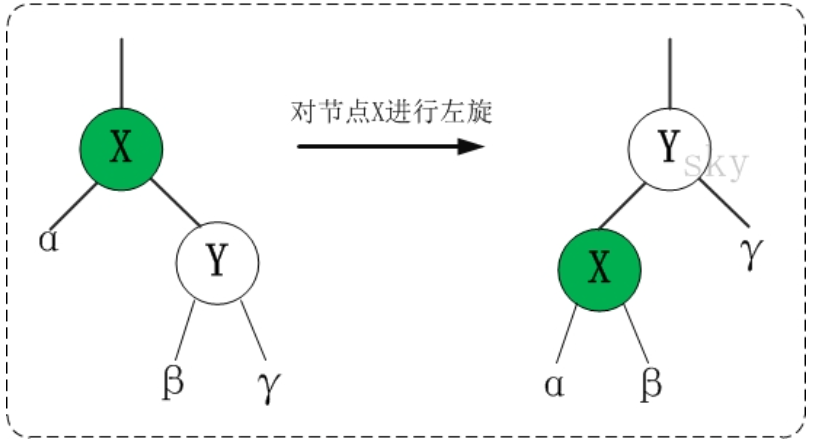
2:右旋转:(如下图:图片来源网络)
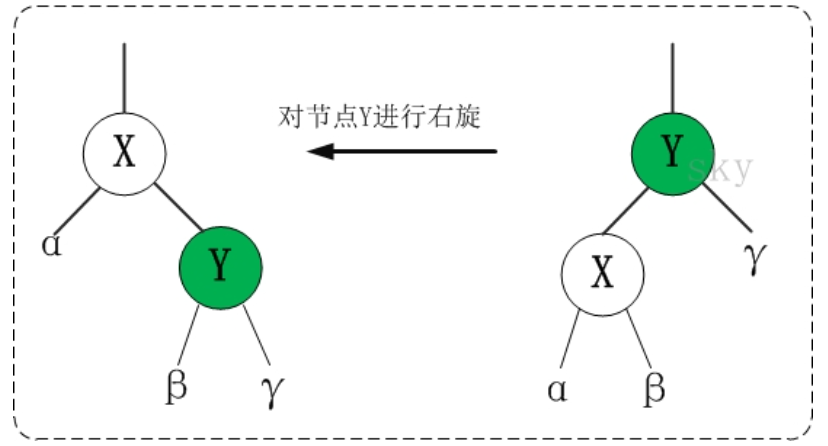
3:变色:通过改变节点的颜色达到满足红黑树的概念。
1.3:红黑树的应用
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。 例如,Java集合中的TreeSet,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
2:红黑树的插入操作
2.1插入
插入总共可以分为五种情况,其中前两种情况是最简单的,而后面的情况又是可以相互转换的,下面具体分析。为了使插入之后尽量满足红黑树更多的规则,所以我们规定每个新插入的节点为红色。
(第三四五种情况我们按照在如下前提下进行:插入的节点为S(son),S的父亲节点为F(father),F的父亲节点为G(grandfather),而F的兄弟节点为U(uncle)。并且F为G的左儿子) 当F为G的右儿子的时候对称操作即可。
2.1.1:为跟节点
若新插入的节点N没有父节点,则直接当做根据节点插入即可,同时将颜色设置为黑色。
2.1.2:父节点为黑色
这种情况新节点N同样是直接插入,同时颜色为红色,由于根据规则四它会存在两个黑色的叶子节点,值为null。同时由于新增节点N为红色,所以通过它的子节点的路径依然会保存着相同的黑色节点数,同样满足规则5。
2.1.3:若父节点F和F的兄弟节点U都为红色
操作:将F以及U设置为黑,G设为红,并将G看成新插入的节点(即下一轮的S),递归操作。
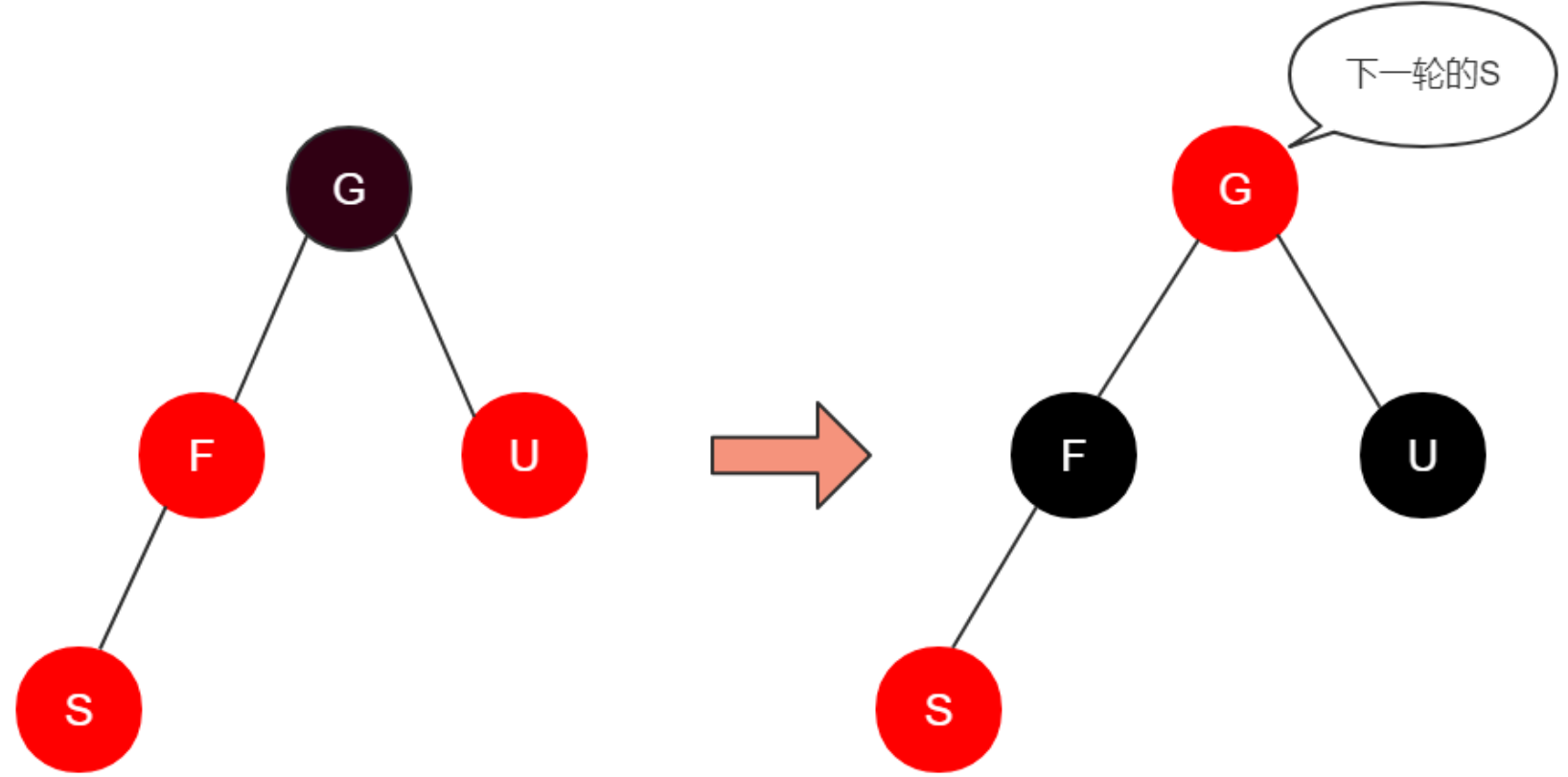
原因:这个操作实际是想将红色往根处移动。将红色往上移了一层,并不会打破红黑树的特性,不断的把红色往上移动,当移动到根时,直接将根设置为黑色,就完全符合红黑树的性质了。
2.1.4:若父节点F为红色,叔节点U为黑色或者缺少,且新增节点S为F节点的右孩子
操作:将F左旋,并把F看成新加入的节点(即下一轮的S),继续后面的判断。
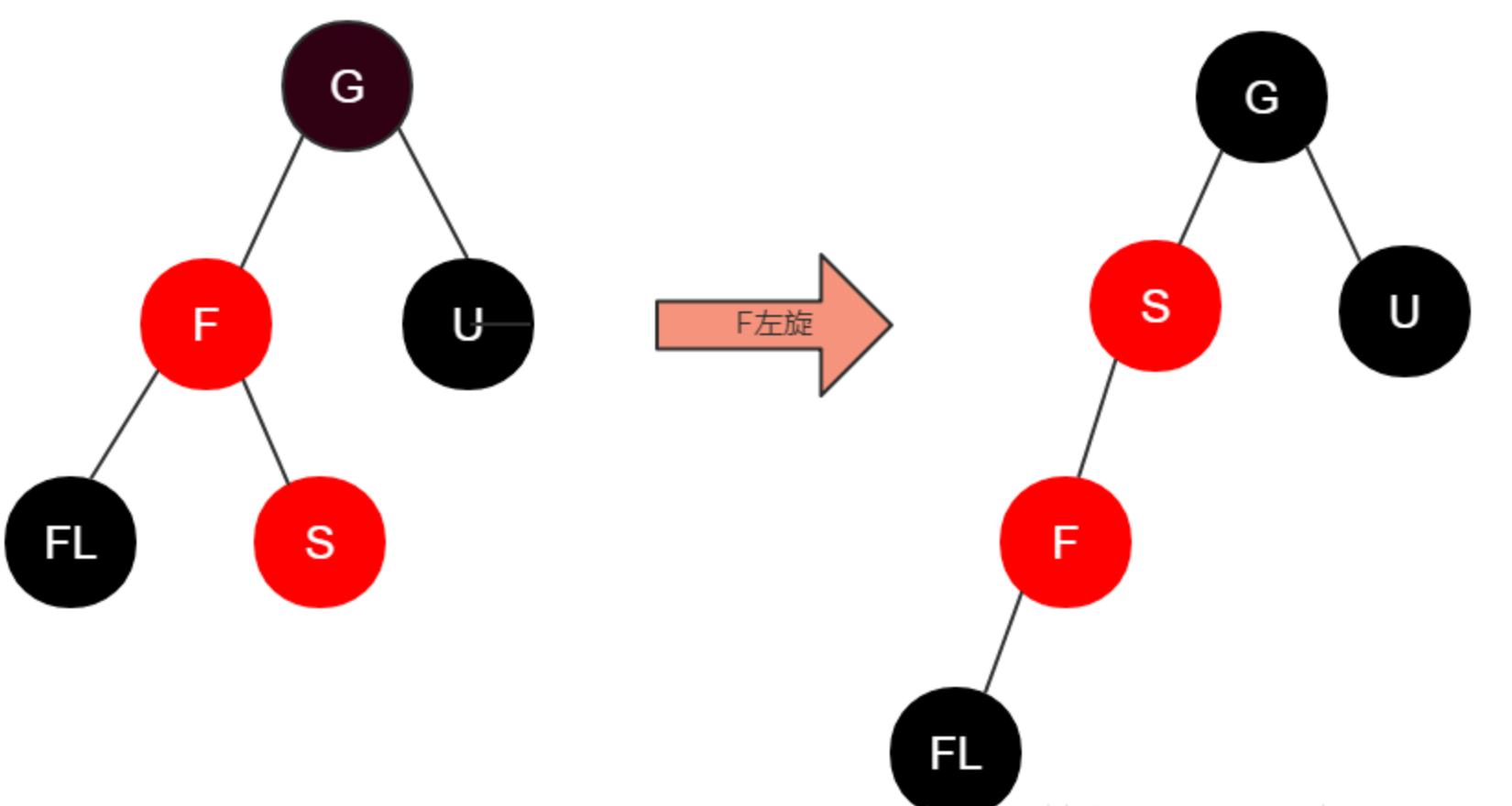
这里所产生的结果其实并没有完成,还不是平衡的(违反了规则四),这是我们需要进行情况5的操作。
2.1.5:父节点F为红色,叔父节点U为黑色或者缺少,新增节点S为父节点F左孩子
操作:先将F设为黑,G设为红,然后G右旋。这样操作后,就完全符合红黑树的性质了

3:Java中TreeMap插入操作实现分析
本来想自己手动实现一下红黑树,奈何JDK源码写的太优秀了,下面就结合Java中TreeMap的put方法实现分析上面的操作。
3.1:插入操作
public V put(K key, V value) {
Entry<K,V> t = root;
//第一种情况也就是上满的2.1.1
if (t == null) {
//本来感觉这句代码没有用,看到源码注释才知道校验空值用的,真是的。。。。。。。
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
//cmp表示key比较大小的返回结果
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
//如果cpr不为空,则采用既定的排序算法进行创建TreeMap集合
if (cpr != null) {
//该循环是根据给定的排序算法根据key是否能找到对应的键值对,如果能找到的话则覆盖旧值并且返回旧值
do {
//parent为找到的符合插入的父节点
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//如果cpr为空,则采用默认的排序算法进行创建TreeMap集合
else {
if (key == null)
throw new NullPointerException();
