TopN算法，流式数据获取前N条数据

　　背景：由于业务需求，用户想要统计每周，每月，几个月，一年之中的前N条数据。
　　根据已有的思路无非就是对全部的数据进行排序，然后取出前N条数据，可是这样的话按照目前最优的排序算法复杂度也在O(nlog(n)),而且如果把所有的数据都放到内存之中排序，数据量太大的话可能不仅仅是慢，还可能因为占用内存过大而导致OOM而产生不可预估的影响。
如果利用分而治之的思想，把所有的数据都存储到磁盘之中，然后数据平均分成M个文件,这样可以利用分批次算出每一个文件之中的前N条数据，然后在合并。但是这样会多次读取磁盘，无形之中增加了多次IO，所以效率也不是很乐观。
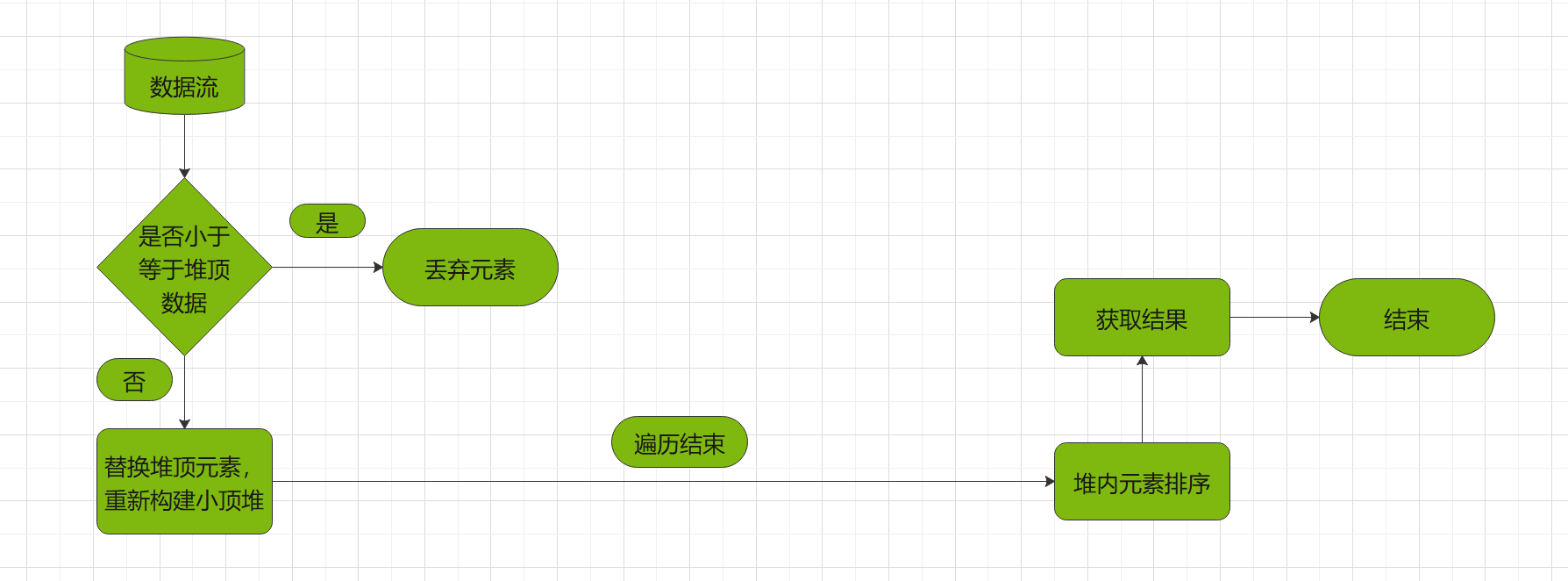
　　在仔细思考各种排序算法之后，发现我们可以借鉴堆排序算法，采用堆排序，而不采用其他排序算法的原因就是堆排序是分成了两部分。首先构建小/大顶堆，然后在对小/大顶堆进行排序。比如我们可以想要从N条数据中得最大的前Q条数据，那我们就可以构建一个大小为Q的小顶堆，先不对其进行排序，继续读取数据，如果读取的数据小于堆顶数据，直接略过，如果大于对顶数据，则替换堆顶数据，重新构建小/大顶堆。至此，当数据遍历完成，在堆中的所有数据便是最大的前Q条数据，只需对着前十条数据排序即可。这个时间复杂度最大是O(nlog(Q)),最小是O(n)。

 

如有对堆排序不了解的同学，请自行询问度娘，这里不再解释。

堆排序代码参考：https://baike.baidu.com/item/%E5%A0%86%E6%8E%92%E5%BA%8F/2840151?fr=aladdin

 

下面是得到对打的前N条数据的流程图：

 

下面是代码实现：

交换元素代码

/**
 * 交换元素
 *
 * @param arr arr
 * @param a   元素的下标
 * @param b   元素的下标
 * @return void
 * @author liekkas
 */
private void swap(int[] arr, int a, int b) {
    arr[a] = arr[a] ^ arr[b];
    arr[b] = arr[a] ^ arr[b];
    arr[a] = arr[a] ^ arr[b];
}

整个堆排序最关键的地方  以当前节点为根节点构建小顶堆

/**
     * 整个堆排序最关键的地方  以当前节点为根节点构建小顶堆
     *
     * @param array  待组堆
     * @param i      起始结点
     * @param length 堆的长度
     * @return void
     * @author liekkas
     */
    private void adjustMinHeap(int[] array, int i, int length) {
        // 先把当前元素取出来，因为当前元素可能要一直移动
        int temp = array[i];
        for (int k = 2 * i + 1; k < length; k = 2 * k + 1) {
            //2*i+1为左子树i的左子树(因为i是从0开始的),2*k+1为k的左子树
            // 让k先指向子节点中最小的节点
            if (k + 1 < length && array[k] > array[k + 1]) {
                //如果有右子树,并且右子树大于左子树
                k++;
            }
            //如果发现结点(左右子结点)大于根结点，则进行值的交换
            if (array[k] < temp) {
                swap(array, i, k);
                // 如果子节点更换了，那么，以子节点为根的子树会受到影响,所以，循环对子节点所在的树继续进行判断
                i = k;
            } else {  //不用交换，直接终止循环
                break;
            }
        }
    }

构建小顶堆

/**
 * 构建小顶堆
 *
 * @param array 待构建数组
 * @return void
 * @author liekkas
 */
private void buildMinHeap(int[] array) {

    //这里元素的索引是从0开始的,所以最后一个非叶子结点array.length/2 - 1
    for (int i = array.length / 2 - 1; i >= 0; i--) {
        //调整堆
        adjustMinHeap(array, i, array.length);
    }
}

堆排序

/**
 * 堆排序
 *
 * @param array 待排序数组
 * @return int[] 已排序数组
 * @author liekkas
 */

private int[] sort(int[] array) {

    buildMinHeap(array);

    // 上述逻辑，建堆结束
    // 下面，开始排序逻辑
    for (int j = array.length - 1; j > 0; j--) {
        // 元素交换,作用是去掉大顶堆
        // 把大顶堆的根元素，放到数组的最后；换句话说，就是每一次的堆调整之后，都会有一个元素到达自己的最终位置
        swap(array, 0, j);
        // 元素交换之后，毫无疑问，最后一个元素无需再考虑排序问题了。
        // 接下来我们需要排序的，就是已经去掉了部分元素的堆了，这也是为什么此方法放在循环里的原因
        // 而这里，实质上是自上而下，自左向右进行调整的
        adjustMinHeap(array, 0, j);
    }
    return array;
}

 

测试代码：

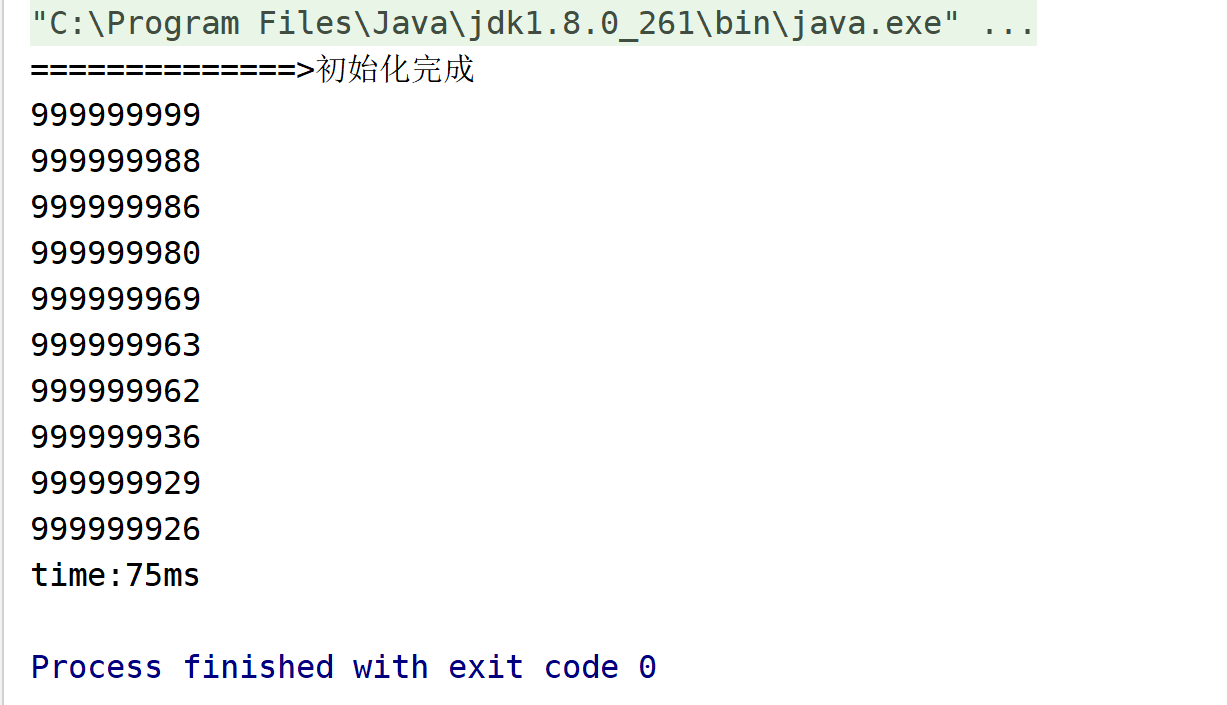
    public static void main(String[] args) {
        HeapSort heapSort = new HeapSort();
        int len = 100000000;
        int topN = 10;
        Random random = new Random();
        int[] arr = new int[len];
        int[] topArr = new int[topN];
        //生成随机数组
        for (int i = 0; i < len; i++) {
            arr[i] = random.nextInt(1000000000);

        }

        //初始化数组
        System.arraycopy(arr, 0, topArr, 0, topN);

        System.out.println("==============>初始化完成");
        long start = System.currentTimeMillis();

        heapSort.buildMinHeap(topArr);
        for (int i = 0; i < len; i++) {
            if (arr[i] > topArr[0]) {
                topArr[0] = arr[i];
                heapSort.buildMinHeap(topArr);
            }
        }

        int[] sort = heapSort.sort(topArr);

        long end = System.currentTimeMillis();
        for (int i : sort) {
            System.out.println(i);
        }

        System.out.println("time:" + (end - start) + "ms");
    }

测试结果：