机器学习——神经网络
###神经网络基础概念
人工神经网络又叫神经网络，是借鉴了生物神经网络的工作原理形成的一种数学模型。神经网络是机器学习诸多算法中的一种，它既可以用来做有监督的任务，如分类、视觉识别等，也可以用作无监督的任务。同时它能够处理复杂的非线性问题，它的基本结构是神经元，如下图所示：
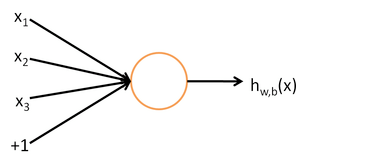
其中，x1、x2、x3代表输入，中间部分为神经元，而最后的hw,b(x)是神经元的输出。整个过程可以理解为输入——>处理——>输出。
由多个神经元组成的就是神经网络
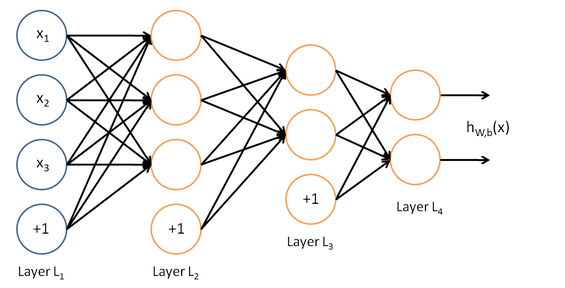
如图所示：
这是一个4层结构的神经网络，layer1为输入层，layer4为输出层，layer2,layer3为隐藏层，即神经网络的结构由输入层，隐藏层，输出层构成。其中除了输入层以外，每一层的输入都是上一层的输出。
###神经网络数学原理
单个神经元的数学构成很简单，包含两个部分权重和偏置，每个输入值进入神经元都会进行类似y=wx+b其中w为权重，b为偏置，x为输入值，y为单个输入值的结果，经过激活函数激活后输出结果为f(wx+b),其中f为激活函数。存在多个输入值使用激活函数的情况下输出值为f(w1x1+w2x2+...+wnxn+b)。
激活函数的作用
激活函数也成为映射函数，可以对计算结果进行非线性转换，从而提升神经网络的表达能力，从而能够处理线性不可分的问题，比如语音识别和图像识别等。常见的激活函数有sigmoid,tanh,relu...等。
####激活函数之sigmoid
sigmoid的表达式为：
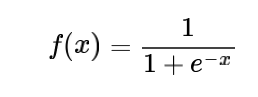
其图形为一个s型曲线，会将所有的输入结果映射到0-1之间，图形样式如下：
sigmoid常备用于处理二分类问题，比较典型的像逻辑回归就是使用sigmoid处理二分类问题。
####激活函数之tanh
tanh的表达式为：
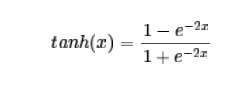
tanh函数的图形和sigmoid类似，不同的是它是将输入值映射到-1~1之间。它的图形如下图所示：
由于tanh函数的压缩范围在-1~1之间，因而它的输出基本是0均值，即下一层的输入为0均值，这使得tanh函数的收敛速度要快于sigmoid函数。
假设后层神经元的输入都为正(e.g. x>0 elementwise in f=wTx+b),那么对w求局部梯度则都为正，这样在反向传播的过程中w要么都往正方向更新，要么都往负方向更新，导致有一种捆绑的效果，使得收敛缓慢。这是sigmoid函数容易出现的问题，而tanh函数的映射特点很好的避开了这个问题。因而在实际使用中，人们会更经常使用tanh函数作为激活函数。
sigmoid函数和tanh函数的共同问题是在求导过程中可能出现梯度消失的现象。
####激活函数之ReLU
ReLU的表达式为：
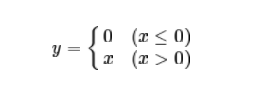
根据表达式描绘它的图形也很简单，如下图所示：
它相比于sigmoid和tanh有更快的收敛速度，同时不会出现梯度消失的问题。另外从函数表达中可以知道，输入小于0时，输出会变成0，这就使得神经网络变得稀疏，并减少参数的相互依存关系，缓解过拟合问题，而且由于函数的本身特性，不涉及指数等操作，实现起来也更加容易。
但它也有缺点，ReLU单元脆弱且可能会在训练中死去。例如，大的梯度流经过ReLU单元时可能导致神经不会在以后任何数据节点再被激活。当这发生时，经过此单元的梯度将永远为零。ReLU单元可能不可逆地在训练中的数据流中关闭。例如，比可能会发现当学习速率过快时你40%的网络都“挂了”（神经元在此后的整个训练中都不激活）。当学习率设定恰当时，这种事情会更少出现。
###反向传播
反向传播的目的在于通过不断的回传误差，对权重进行更新，重新计算输出，最终从已有的输入值经过神经网络得到我们需要的结果。要理解反向传播，我们需要先理解前向传播的过程。
假设一个三层神经网络，在随机分配获得权重的情况下，数据从输入层——>隐藏层——>输出层过程可以称为前向传播，当然在这个过程中会涉及很多数学计算，最终会在输出层有一个输出值，而输出值和我们需要的目标值或实际值之间一般会存在差距，即我们通常说的误差。
接下来，根据误差进行反向更新权值的过程就称之为误差的反向传播，要对权值进行更新，我们需要评估权值对误差产生的影响大小，这个通过计算误差对权值的偏导值进行估计，过程中有一个重要的概念是链式法则。
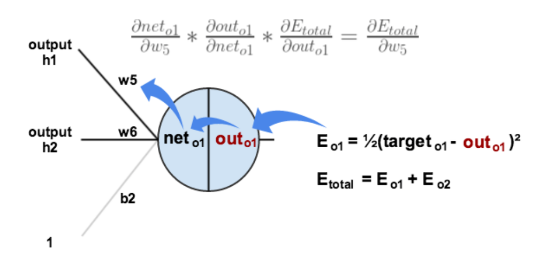
其中链式求导表现为：
即误差对权值的偏导值可以看成每一个反向计算步骤的偏导值的乘积。
在得到误差对权值的偏导值后，我们就可以对权值进行更新，更新公式为：
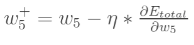
其中n是学习速率。
按照相同的步骤对所有的权重进行更新，然后再次进行前向传播，获得新误差，再反向传播更新权值，不断的重复这个过程，直到误差达到我们设定的阈值范围结束迭代。
参考资料：
一文弄懂神经网络中的反向传播法——BackPropagation
https://www.cnblogs.com/charlotte77/p/5629865.html
