数据结构——关于图的存储中十字链表和邻接多重表的理解和思考

有向图的十字链表

对于有向图来说，邻接表是有缺陷的，关心了出度问题，想了解入度就必须要遍历整个图才能知道，反之，逆邻接表解决了入度的情况。

把邻接表与逆邻接表结合起来，即有向图的一种存储方法十字链表(Orthogonal   List)。

我们重新定义顶点表结构

firstin表示入边表头指针，指向该顶点的入边表中第一个结点；

firstout表示出边表头指针，指向该顶点的出边表中第一个结点；

重新定义了边表结点结构

其中

tailvex是指弧起点在顶点的下标，

headvex是指弧终点在顶点表中的下标，

headlink是指入边表指针域，指向终点相同的一下条边

taillink是指出边表指针域，指向起点相同的下一条边。

如果是网，还可以再增加一个weight域来存储权值。

 

如图对于这样的一个有向图，构建如下的十字链表

 

 

对于十字链表的一些认识：

1.表头结点即顶点结点，与邻接表一样是顺序存储。

2.对于每个顶点结点之后是与之相关联的弧结点（该弧结点中存有弧头、弧尾），而邻接表则是一些与顶点结点相连接的点。

3.从每个顶点结点开始有两条链表，一条是以该顶点结点为弧头的链表，一条是以该顶点结点为弧尾的链表。

4.对于其中的每一条链表必然是从顶点结点开始，直到与之相关的弧结点链域headlink和taillink为空是结束，构成一条完整的链表。

十字链表存储结构：

typedef struct ArcBox   // 弧的结构表示
{
    int tailvex, headvex;
    InfoType  *info;
    struct ArcBox  *hlink, *tlink;
} VexNode;
typedef struct VexNode   // 顶点的结构表示
{
    VertexType  data;
    ArcBox  *firstin, *firstout;
} VexNode;

typedef struct
{
    VexNode  xlist[MAX_VERTEX_NUM];// 顶点结点(表头向量)
    int   vexnum, arcnum;//有向图的当前顶点数和弧数
} OLGraph;

十字链表的好处就是因为把邻接表和逆邻接表整合在一起，这样既容易找到vi为尾的弧，也容易打到以vi为头的弧，因而容易求得顶点的出度和入度。而且它除了结构复杂一点燃上，其实创建图的算法的时间复杂度与邻接表相同，因此，在有向图的应用中，十字链表是非常好的数据结构模型。

 

无向图的邻接多重表

 

对于无向图的边操作，如下图要删除(v0,v2)这条边要做

 

需要对邻接表结构中右边表的阴影两个结点进行删除操作，显然比较烦琐

因此，我们也仿照十字链表的方式对边表结构进行一些改造，也许就可避免刚才的问题。

重新定义边表结构：

 

其中mark是标志域，用于标记该条边是否访问过。ivex和jvex是与某条边依附的两个顶点在顶点表中的下标。ilink指向依附顶点ivex的下条边，jlink指向依附顶点的下一条边。这就是邻接多重表结构。

 对于顶点结构不变，也是用一个结点表示，由存储与该结点信息相关的域date和指示第一条依附于该结点的边的域firstedge构成。

 

我们来看结构示意图的绘制过程，理解了它是如何连线的，也就是理解邻接多重表构造原理了。

 

 

 

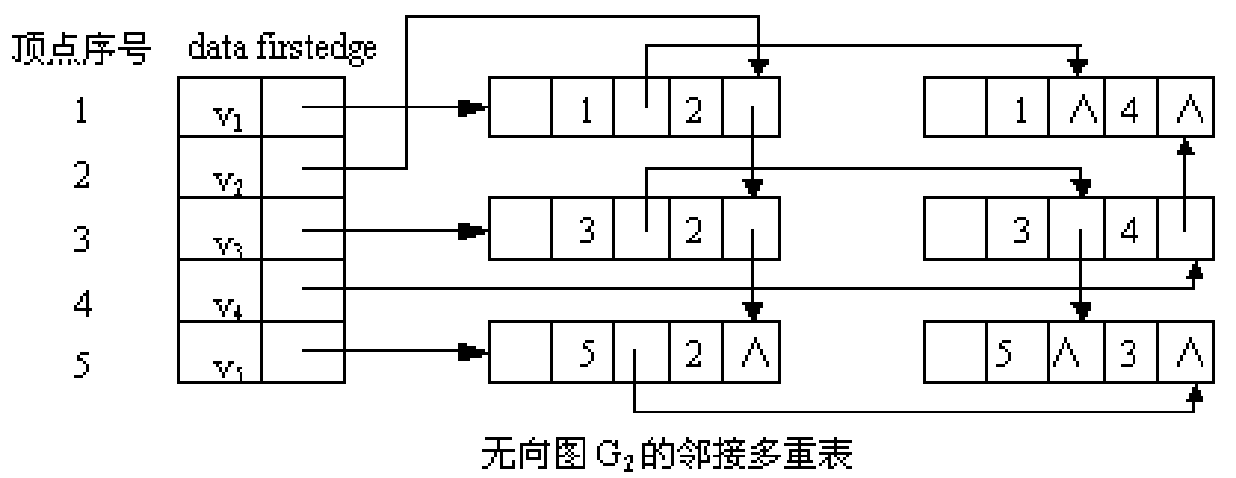
对于邻接多重表的一些认识：

1.表头结点即顶点结点，与邻接表一样是顺序存储。

2.对于每个顶点结点之后是与之相关联的边结点（与该顶点结点相连的边），而邻接表则是一些与顶点结点相连接的点。

3.从每个顶点结点开始有一条链表，这条链表将所有与该顶点相连的边都连接了起来。

4.邻接多重表中边结点的个数就是无向图中边的数量，又因为无向图中的边必然连接两个顶点，所以便边结点结构中的ilink和jlink会连接两个不同的链表。

 

邻接多重表的存储结构：

typedef struct Ebox
{
    VisitIf  mark;      // 访问标记
    int ivex, jvex;//该边依附的两个顶点的位置
    struct EBox  *ilink, *jlink;
    InfoType *info;          // 该边信息指针
} EBox;
typedef struct VexBox
{
    VertexType  data;
    EBox  *firstedge; // 指向第一条依附该顶点的边
} VexBox;
typedef struct    // 邻接多重表
{
    VexBox  adjmulist[MAX_VERTEX_NUM];
    int   vexnum, edgenum;
} AMLGraph;