KMP字符串匹配算法

去年冬天就接触KMP算法了，但是听的不明不白，遇到字符串匹配的题我大都直接使用string中的find解决了，但今天数据结构课又讲了一下，我觉得有必要再来回顾一下。之前看过很多关于KMP的博客，有很多虽然很好，但是要么太专业，要么很难想象，这篇博客用了大量的图示例子来说明，主要在于启发，后面给出代码说明。

主要参考：
http://www.ruanyifeng.com/blog/2013/05/Knuth–Morris–Pratt_algorithm.html
https://www.cnblogs.com/yjiyjige/p/3263858.html
https://www.cnblogs.com/aiguona/p/9133865.html

KMP算法引入：

KMP是三位大牛：D.E.Knuth、J.H.Morris和V.R.Pratt同时发现的。

KMP算法要解决的问题就是在字符串（也叫主串）中的模式（pattern）定位问题。说简单点就是我们平时常说的关键字搜索。模式串就是关键字（接下来称它为P），如果它在一个主串（接下来称为T）中出现，就返回它的具体位置，否则返回-1（常用手段）。

首先，对于这个问题有一个很单纯的想法：从左到右一个个匹配，如果这个过程中有某个字符不匹配，就跳回去，将模式串向右移动一位。这有什么难的？

我们可以这样初始化：

之后我们只需要比较i指针指向的字符和j指针指向的字符是否一致。如果一致就都向后移动，如果不一致，如下图：

A和E不相等，那就把i指针移回第1位（假设下标从0开始），j移动到模式串的第0位，然后又重新开始这个步骤：

基于这个想法我们可以得到以下的程序：

public static int bf(String ts, String ps){
    int i = 0; // 主串的位置
    int j = 0; // 子串的位置
    while (i < t.length && j < p.length){
    // 当两个字符相同，就比较下一个
        if (t[i] == p[j]){
            i++;
            j++;
        }else{
            i = i - j + 1;///一旦不匹配，i后退
            j = 0; ///j归0
        }

    }
    if (j == p.length){
        return i - j;///匹配成功返回子串在母串最先出现的位置
    }
    else{
        return -1;///不成功返回-1
    }
}

然而这并不是一种优秀的算法，因为会出现指针的回退，一旦匹配不成功就要退回子串的其实位置，而之前完成的部分匹配也将作废，时间复杂度为O（n*m）。

而KMP算法却能将时间复杂度优化为O(n+m)，它是怎么做到的呢？我们再举一个例子。

（1）对于已经匹配到这种状态的两个字符串：

一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是，设法利用这个已知信息，不要把"搜索位置"移回已经比较过的位置，继续把它向后移，这样就提高了效率。

（2）

怎么做到这一点呢？可以针对搜索词，算出一张《部分匹配表》（Partial Match Table）。这张表是如何产生的，后面再介绍，这里只要会用就可以了。

（3）

已知空格与D不匹配时，前面六个字符"ABCDAB"是匹配的。查表可知，最后一个匹配字符B对应的"部分匹配值"为2，因此按照下面的公式算出向后移动的位数：

移动位数 = 已匹配的字符数 - 对应的部分匹配值

因为 6 - 2 等于4，所以将搜索词向后移动4位。

(4)

因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（"AB"），对应的"部分匹配值"为0。所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位。

(5)

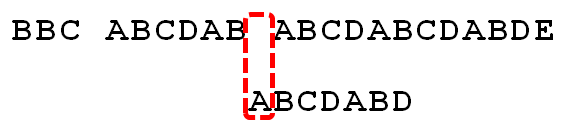
因为空格与A不匹配，继续后移一位。

(6)

逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动4位。

(7)

逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 - 0，再将搜索词向后移动7位，这里就不再重复了。

下面介绍《部分匹配表》是如何产生的。

首先，要了解两个概念："前缀"和"后缀"。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例，

• "A"的前缀和后缀都为空集，共有元素的长度为0；
• "AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；
• "ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；
• "ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；
• "ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；
• "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；
• "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

为了记录这些信息我们使用了一个next数组来记录每一个字符的部分匹配值。

最后在对基本原理进行一下说明：

"部分匹配"的实质是，有时候，字符串头部和尾部会有重复。比如，"ABCDAB"之中有两个"AB"，那么它的"部分匹配值"就是2（"AB"的长度）。搜索词移动的时候，第一个"AB"向后移动4位（字符串长度-部分匹配值），就可以来到第二个"AB"的位置。这也是我认为KMP算法最为厉害的地方，利用字符串自身具有的重复性避免了指针的回退！！！

kmp算法的核心即是计算子串F每一个位置之前的字符串的前缀和后缀公共部分的最大长度（不包括字符串本身，否则最大长度始终是字符串本身）。

获得F每一个位置的最大公共长度之后，就可以利用该最大公共长度快速和字符串S比较。当每次比较到两个字符串的字符不同时，我们就可以根据最大公共长度将字符串F向前移动(已匹配长度-最大公共长度)位，接着继续比较下一个位置。事实上，字符串F的前移只是概念上的前移，只要我们在比较的时候从最大公共长度之后比较F和S即可达到字符串f前移的目的。

代码说明：

获得next数组:

void cal_next(char *str, int *next, int len)
{
    next[0] = -1;///next[0]初始化为-1，-1表示不存在相同的最大前缀和最大后缀
    int k = -1;///k初始化为-1
    for (int q = 1; q <= len-1; q++)
    {
        while (k > -1 && str[k + 1] != str[q])///如果下一个不同，那么k就变成next[k]，注意next[k]是小于k的，无论k取任何值。
        {
            k = next[k];//往前回溯
        }
        if (str[k + 1] == str[q])//如果相同，k++
        {
            k = k + 1;
        }
        next[q] = k;///这个是把算的k的值（就是相同的最大前缀和最大后缀长）赋给next[q]
    }
}

kmp主函数：

 void cal_next(char *str, int *next, int len)
{
    next[0] = -1;///next[0]初始化为-1，-1表示不存在相同的最大前缀和最大后缀
    int k = -1;///k初始化为-1
    for (int q = 1; q <= len-1; q++)
    {
        while (k > -1 && str[k + 1] != str[q])///如果下一个不同，那么k就变成next[k]，注意next[k]是小于k的，无论k取任何值。
        {
            k = next[k];//往前回溯
        }
        if (str[k + 1] == str[q])//如果相同，k++
        {
            k = k + 1;
        }
        next[q] = k;///这个是把算的k的值（就是相同的最大前缀和最大后缀长）赋给next[q]
    }
}

代码说明：

这一段代码可以说是KMP算法的精髓， 这里给出以下说明。

while (k > -1 && str[k + 1] != str[q]){
    k = next[k];
}

看cal_next(..)函数：
首先我们看第一个while循环，它到底干了什么。
在此之前，我们先回到原程序。原程序里有一个大的for()循环，那这个for()循环是干嘛的？
这个for循环就是计算next[0]，next[1],…next[q]…的值。
里面最后一句next[q]=k就是说明每次循环结束，我们已经计算了ptr的前(q+1)个字母组成的子串的“相同的最长前缀和最长后缀的长度”。这个“长度”就是k。
好，到此为止，假设循环进行到 第 q 次，即已经计算了next[q]，我们是怎么计算next[q+1]呢？
比如我们已经知道ababab，q=4时，next[4]=2（k=2，表示该字符串的前5个字母组成的子串ababa存在相同的最长前缀和最长后缀的长度是3，所以k=2,next[4]=2。
这个结果可以理解成我们自己观察算的，也可以理解成程序自己算的，这不是重点，重点是程序根据目前的结果怎么算next[5]的）。那么对于字符串ababab，我们计算next[5]的时候，此时q=5, k=2（上一步循环结束后的结果）。
那么我们需要比较的是str[k+1]和str[q]是否相等，其实就是str[1]和str[5]是否相等！，为啥从k+1比较呢，因为上一次循环中，我们已经保证了str[k]和str[q]（注意这个q是上次循环的q）是相等的（这句话自己想想，很容易理解），所以到本次循环，我们直接比较str[k+1]和str[q]是否相等（这个q是本次循环的q）。
如果相等，那么跳出while()，进入if()，k=k+1，接着next[q]=k。即对于ababab，我们会得出next[5]=3。
如果不等，我们可以用”ababac“描述这种情况。不等，进入while()里面，进行k=next[k]，这句话是说，在str[k + 1] != str[q]的情况下，我们往前找一个k，使str[k + 1]==str[q]。程序给出了一种找法，那就是 k = next[k]。
程序的意思是说，一旦str[k + 1] != str[q]，即在后缀里面找不到时，我是可以直接跳过中间一段，跑到前缀里面找，next[k]就是相同的最长前缀和最长后缀的长度。所以，k=next[k]就变成，k=next[2]，即k=0。
此时再比较str[0+1]和str[5]是否相等，不等，则k=next[0]=-1。跳出循环。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
void cal_next(char *str, int *next, int len)
{
    next[0] = -1;
    int k = -1;
    for (int q = 1; q <= len-1; q++)
    {
        while (k > -1 && str[k + 1] != str[q])
        {
            k = next[k];
        }
        if (str[k + 1] == str[q])
        {
            k = k + 1;
        }
        next[q] = k;
    }
}
int KMP(char *str, int slen, char *ptr, int plen)
{
    int *next = new int[plen];
    cal_next(ptr, next, plen);
    int k = -1;
    for (int i = 0; i < slen; i++)
    {
        while (k >-1&& ptr[k + 1] != str[i])
            k = next[k];
        if (ptr[k + 1] == str[i])
            k = k + 1;
        if (k == plen-1)
        {
            //cout << "在位置" << i-plen+1<< endl;
            //k = -1;//重新初始化，寻找下一个
            //i = i - plen + 1;//i定位到该位置，外层for循环i++可以继续找下一个（这里默认存在两个匹配字符串可以部分重叠）
            return i-plen+1;
        }
    }
    return -1;
}
int main()
{
    char *str = "bacbababadababacambabacaddababacasdsd";
    char *ptr = "ababaca";
    int a = KMP(str, 36, ptr, 7);
    printf("%d",a);
    return 0;
}