中国剩余定理

暑假集训的时候就应该来写这篇博客的，当时听的有些糊涂，不过该来的还是得来。。。

中国剩余定理介绍

在《孙子算经》中有这样一个问题：“今有物不知其数，三三数之剩二（除以3余2），五五数之剩三（除以5余3），七七数之剩二（除以7余2），问物几何？”这个问题称为“孙子问题”，该问题的一般解法国际上称为“中国剩余定理”。

在《孙子歌诀》中给出了解决这个问题的解法：三人同行七十稀，五树梅花廿一支，七子团圆正半月，除百零五便得知。很是朗朗上口，但这是什么意思呢？

具体解法分三步：

找出三个数：

1.从3和5的公倍数中找出被7除余1的最小数15，从3和7的公倍数中找出被5除余1 的最小数21，最后从5和7的公倍数中找出除3余1的最小数70。

2.用15乘以2（2为最终结果除以7的余数），用21乘以3（3为最终结果除以5的余数），同理，用70乘以2（2为最终结果除以3的余数），然后把三个乘积相加（15*2+21*3+70*2）得到和233。

3.用233除以3，5，7三个数的最小公倍数105，得到余数23，即233%105=23。这个余数23就是符合条件的最小数。

就这么简单。我们在感叹神奇的同时不禁想知道古人是如何想到这个方法的，有什么基本的数学依据吗？

中国剩余定理分析

我们将“孙子问题”拆分成几个简单的小问题，从零开始，试图揣测古人是如何推导出这个解法的。

     首先，我们假设n1是满足除以3余2的一个数，比如2，5，8等等，也就是满足3*k+2（k>=0）的一个任意数。同样，我们假设n2是满足除以5余3的一个数，n3是满足除以7余2的一个数。

     有了前面的假设，我们先从n1这个角度出发，已知n1满足除以3余2，能不能使得 n1+n2 的和仍然满足除以3余2？进而使得n1+n2+n3的和仍然满足除以3余2？

     这就牵涉到一个最基本数学定理，如果有a%b=c,则有(a+kb)%b=c(k为非零整数)，换句话说，如果一个除法运算的余数为c，那么被除数与k倍的除数相加（或相减）的和（差）再与除数相除，余数不变。这个是很好证明的。

     以此定理为依据，如果n2是3的倍数，n1+n2就依然满足除以3余2。同理，如果n3也是3的倍数，那么n1+n2+n3的和就满足除以3余2。这是从n1的角度考虑的，再从n2，n3的角度出发，我们可推导出以下三点：

  1. 为使n1+n2+n3的和满足除以3余2，n2和n3必须是3的倍数。
  2. 为使n1+n2+n3的和满足除以5余3，n1和n3必须是5的倍数。
  3. 为使n1+n2+n3的和满足除以7余2，n1和n2必须是7的倍数。

    因此，为使n1+n2+n3的和作为“孙子问题”的一个最终解，需满足：

  1. n1除以3余2，且是5和7的公倍数。
  2. n2除以5余3，且是3和7的公倍数。
  3. n3除以7余2，且是3和5的公倍数。

    所以，孙子问题解法的本质是从5和7的公倍数中找一个除以3余2的数n1，从3和7的公倍数中找一个除以5余3的数n2，从3和5的公倍数中找一个除以7余2的数n3，再将三个数相加得到解。在求n1，n2，n3时又用了一个小技巧，以n1为例，并非从5和7的公倍数中直接找一个除以3余2的数，而是先找一个除以3余1的数，再乘以2。

    这里又有一个数学公式，如果a%b=c，那么（a*k）%b=a%b+a%b+…+a%b=c+c+…+c=kc（k>0）,也就是说，如果一个除法的余数为c，那么被除数的k倍与除数相除的余数为kc。展开式中已证明。

    最后，我们还要清楚一点，n1+n2+n3只是问题的一个解，并不是最小的解。如何得到最小解？我们只需要从中最大限度的减掉3，5，7的公倍数105即可。道理就是前面讲过的定理“如果a%b=c,则有(a-kb)%b=c”。所以（n1+n2+n3）%105就是最终的最小解。

 经过分析发现，中国剩余定理的孙子解法并没有什么高深的技巧，就是以下两个基本数学定理的灵活运用：

  1. 如果 a%b=c , 则有 (a+kb)%b=c (k为非零整数)。
  2. 如果 a%b=c，那么 (a*k)%b=kc (k为大于零的整数)。

数学分析

用现代数学的语言来说明的话，中国剩余定理给出了以下的一元线性同余方程组：


中国剩余定理说明：假设整数m1, m2, ... , mn两两互质，则对任意的整数：a1, a2, ... , an，方程组(S)有解，并且通解可以用如下方式构造得到：

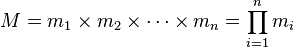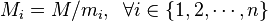  1. 设M = m_1 \times m_2 \times \cdots \times m_n = \prod_{i=1}^n m_i是整数m1, m2, ... , mn的乘积，并设M_i = M/m_i, \; \; \forall i \in \{1, 2, \cdots , n\}是除了mi以外的n - 1个整数的乘积。
  2. 设t_i = M_i^{-1}为M_i模m_i的数论倒数：t_i M_i \equiv 1 \pmod {m_i}, \; \; \forall i \in \{1, 2, \cdots , n\}.
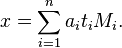
  3. 方程组(S)的通解形式为：x = a_1 t_1 M_1 + a_2 t_2 M_2 + \cdots + a_n t_n M_n + k M= k M + \sum_{i=1}^n a_i t_i M_i, \quad k \in \mathbb{Z}. 在模M的意义下，方程组(S)只有一个解：x = \sum_{i=1}^n a_i t_i M_i.
 1 void exgcd(int a1,int b,int &x,int &y)
 2 {
 3     if(b==0)
 4     {
 5         x=1;
 6         y=0;
 7         return ;
 8     }
 9     exgcd(b,a1%b,x,y);
10     int t=x;
11     x=y;
12     y=t-(a1/b)*y;
13 }
14 int CRT(int a[],int m[],int n)
15 {
16     int M=1,ans=0,t,x,y;
17     for(int i=0; i<n; i++)
18     {
19         M*=m[i];///M为除数乘积
20     }
21     for(int i=0; i<n; i++)
22     {
23         t=M/m[i];///除了mi以外的n-1个整数乘积
24         exgcd(t,m[i],x,y);///求逆元，由扩展欧几里得转换成t*ti+m[i]*y=1来求ti
25         ans=(ans+a[i]*x*t)%M;
26     }
27     return (ans+M)%M;
28 }

 

一个正整数K，给出K Mod 一些质数的结果，求符合条件的最小的K。例如，K % 2 = 1, K % 3 = 2, K % 5 = 3。符合条件的最小的K = 23。

Input

第1行：1个数N表示后面输入的质数及模的数量。（2 <= N <= 10) 
第2 - N + 1行，每行2个数P和M，中间用空格分隔，P是质数，M是K % P的结果。（2 <= P <= 100, 0 <= K < P)Output输出符合条件的最小的K。数据中所有K均小于10^9。Sample Input

3
2 1
3 2
5 3

Sample Output

23
 1 #include<cstdio>
 2 #include<cstring>
 3 #include<algorithm>
 4 #define ll long long int
 5 using namespace std;
 6 void exgcd(ll a1,ll b,ll &x,ll &y)
 7 {
 8     ll t;
 9     if(b==0)
10     {
11         x=1;
12         y=0;
13         return ;
14     }
15     exgcd(b,a1%b,x,y);
16     t=x;
17     x=y;
18     y=t-(a1/b)*y;
19 }
20 ll CRT(ll a[],ll m[],ll n)
21 {
22     ll M=1,ans=0,t,x,y,i;
23     for(i=0; i<n; i++)
24     {
25         M*=m[i];
26     }
27     for(i=0; i<n; i++)
28     {
29         t=M/m[i];
30         exgcd(t,m[i],x,y);
31         ans=(ans+a[i]*x*t)%M;
32     }
33     return (ans+M)%M;
34 }
35 
36 int main()
37 {
38     ll n,i,ans;
39     ll a[10],m[10];
40     scanf("%lld",&n);
41     for(i=0;i<n;i++)
42     {
43         scanf("%lld%lld",&m[i],&a[i]);
44     }
45     ans=CRT(a,m,n);
46     printf("%lld\n",ans);
47     return 0;
48 }

 

posted @ 2018-09-12 10:16  王陸  阅读(10875)  评论(6)  编辑  收藏  举报