LCA最近公共祖先(Tarjan离线算法)
这篇博客对Tarjan算法的原理和过程模拟的很详细。
转载大佬的博客https://www.cnblogs.com/JVxie/p/4854719.html
第二次更新,之前转载的博客虽然胜在详细,但其实还是对递归,集合划分,查找还是有些抽象,刚刚恰好看了千千大佬的一篇博客,他在讲解Tarjan算法的时候,用了不同的颜色来区别不同的集合,我觉得这一点非常的好,现在我自己也对Tarjan算法有了一些理解,使用DFS的目的首先是递归中‘递’过程,不断深搜到底;接着回溯使用并查集划分集合,要找LCA的会被放入一个集合中,其LCA就是这个集合的祖先。
转载千千大佬的个人博客加载在本篇博文之后https://www.dreamwings.cn/lca/4874.html
首先什么是最近公共祖先:
在一棵没有环的树上,每个节点肯定有其父亲节点和祖先节点,而最近公共祖先,就是两个节点在这棵树上深度最大的公共的祖先节点。换
句话说,就是两个点在这棵树上距离最近的公共祖先节点。所以LCA主要是用来处理当两个点仅有唯一一条确定的最短路径时的路径。
有人可能会问:那他本身或者其父亲节点是否可以作为祖先节点呢?
答案是肯定的,很简单,按照人的亲戚观念来说,你的父亲也是你的祖先,而LCA还可以将自己视为祖先节点。
举个例子吧,如下图所示4和5的最近公共祖先是2,5和3的最近公共祖先是1,2和1的最近公共祖先是1。 
这就是最近公共祖先的基本概念了,那么我们该如何去求这个最近公共祖先呢?
通常初学者都会想到最简单粗暴的一个办法:对于每个询问,遍历所有的点,时间复杂度为O(n*q),很明显,n和q一般不会很小。
常用的求LCA的算法有:Tarjan/DFS+ST/倍增
后两个算法都是在线算法,也很相似,时间复杂度在O(logn)~O(nlogn)之间,我个人认为较难理解。
有的题目是可以用线段树来做的,但是其代码量很大,时间复杂度也偏高,在O(n)~O(nlogn)之间,优点在于也是简单粗暴。
这篇博客主要是要介绍一下Tarjan算法(其实是我不会在线...)。
什么是Tarjan(离线)算法呢?顾名思义,就是在一次遍历中把所有询问一次性解决,所以其时间复杂度是O(n+q)。
Tarjan算法的优点在于相对稳定,时间复杂度也比较居中,也很容易理解。
下面详细介绍一下Tarjan算法的基本思路:
1.任选一个点为根节点,从根节点开始。
2.遍历该点u所有子节点v,并标记这些子节点v已被访问过。
3.若是v还有子节点,返回2,否则下一步。
4.合并v到u上。
5.寻找与当前点u有询问关系的点v。
6.若是v已经被访问过了,则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。
遍历的话需要用到dfs来遍历(我相信来看的人都懂吧...),至于合并,最优化的方式就是利用并查集来合并两个节点。
下面上伪代码:
1 Tarjan(u)//marge和find为并查集合并函数和查找函数
2 {
3 for each(u,v) //访问所有u子节点v
4 {
5 Tarjan(v); //继续往下遍历
6 marge(u,v); //合并v到u上
7 标记v被访问过;
8 }
9 for each(u,e) //访问所有和u有询问关系的e
10 {
11 如果e被访问过;
12 u,e的最近公共祖先为find(e);
13 }
14 }
个人感觉这样还是有很多人不太理解,所以我打算模拟一遍给大家看。
建议拿着纸和笔跟着我的描述一起模拟!!
假设我们有一组数据 9个节点 8条边 联通情况如下:
1--2,1--3,2--4,2--5,3--6,5--7,5--8,7--9 即下图所示的树
设我们要查找最近公共祖先的点为9--8,4--6,7--5,5--3;
设f[]数组为并查集的父亲节点数组,初始化f[i]=i,vis[]数组为是否访问过的数组,初始为0; 
下面开始模拟过程:
取1为根节点,往下搜索发现有两个儿子2和3;
先搜2,发现2有两个儿子4和5,先搜索4,发现4没有子节点,则寻找与其有关系的点;
发现6与4有关系,但是vis[6]=0,即6还没被搜过,所以不操作;
发现没有和4有询问关系的点了,返回此前一次搜索,更新vis[4]=1;

表示4已经被搜完,更新f[4]=2,继续搜5,发现5有两个儿子7和8;
先搜7,发现7有一个子节点9,搜索9,发现没有子节点,寻找与其有关系的点;
发现8和9有关系,但是vis[8]=0,即8没被搜到过,所以不操作;
发现没有和9有询问关系的点了,返回此前一次搜索,更新vis[9]=1;
表示9已经被搜完,更新f[9]=7,发现7没有没被搜过的子节点了,寻找与其有关系的点;
发现5和7有关系,但是vis[5]=0,所以不操作;
发现没有和7有关系的点了,返回此前一次搜索,更新vis[7]=1;

表示7已经被搜完,更新f[7]=5,继续搜8,发现8没有子节点,则寻找与其有关系的点;
发现9与8有关系,此时vis[9]=1,则他们的最近公共祖先为find(9)=5;
(find(9)的顺序为f[9]=7-->f[7]=5-->f[5]=5 return 5;)
发现没有与8有关系的点了,返回此前一次搜索,更新vis[8]=1;
表示8已经被搜完,更新f[8]=5,发现5没有没搜过的子节点了,寻找与其有关系的点;

发现7和5有关系,此时vis[7]=1,所以他们的最近公共祖先为find(7)=5;
(find(7)的顺序为f[7]=5-->f[5]=5 return 5;)
又发现5和3有关系,但是vis[3]=0,所以不操作,此时5的子节点全部搜完了;
返回此前一次搜索,更新vis[5]=1,表示5已经被搜完,更新f[5]=2;
发现2没有未被搜完的子节点,寻找与其有关系的点;
又发现没有和2有关系的点,则此前一次搜索,更新vis[2]=1;

表示2已经被搜完,更新f[2]=1,继续搜3,发现3有一个子节点6;
搜索6,发现6没有子节点,则寻找与6有关系的点,发现4和6有关系;
此时vis[4]=1,所以它们的最近公共祖先为find(4)=1;
(find(4)的顺序为f[4]=2-->f[2]=2-->f[1]=1 return 1;)
发现没有与6有关系的点了,返回此前一次搜索,更新vis[6]=1,表示6已经被搜完了;

更新f[6]=3,发现3没有没被搜过的子节点了,则寻找与3有关系的点;
发现5和3有关系,此时vis[5]=1,则它们的最近公共祖先为find(5)=1;
(find(5)的顺序为f[5]=2-->f[2]=1-->f[1]=1 return 1;)
发现没有和3有关系的点了,返回此前一次搜索,更新vis[3]=1;

更新f[3]=1,发现1没有被搜过的子节点也没有有关系的点,此时可以退出整个dfs了。
经过这次dfs我们得出了所有的答案,有没有觉得很神奇呢?是否对Tarjan算法有更深层次的理解了呢?
我们假设在如下树中模拟 Tarjan 过程(节点数量少一点可以画更少的图o( ̄▽ ̄)o)
存在查询: LCA(T,3,4)、LCA(T,4,6)、LCA(T,2,1) 。
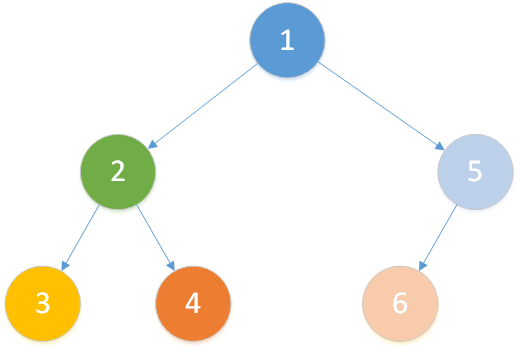
注意:每个节点的颜色代表它当前属于哪一个集合,橙色线条为搜索路径,黑色线条为合并路径。
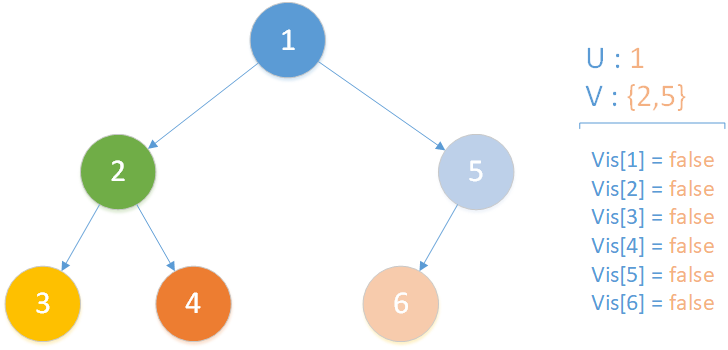
当前所在位置为 u = 1 ,未遍历孩子集合 v = {2,5} ,向下遍历。
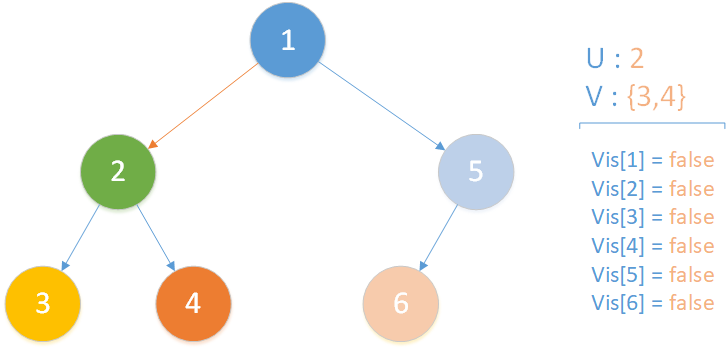
当前所在位置为 u = 2 ,未遍历孩子集合 v = {3,4} ,向下遍历。
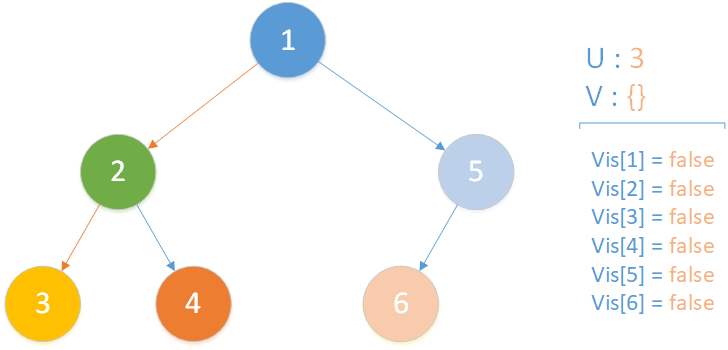
当前所在位置为 u = 3 ,未遍历孩子集合 v = {} ,递归到达最底层,遍历所有相关查询发现存在 LCA(T,3,4) ,但是节点 4 此时标记未访问,因此什么也不做,该层递归结束。
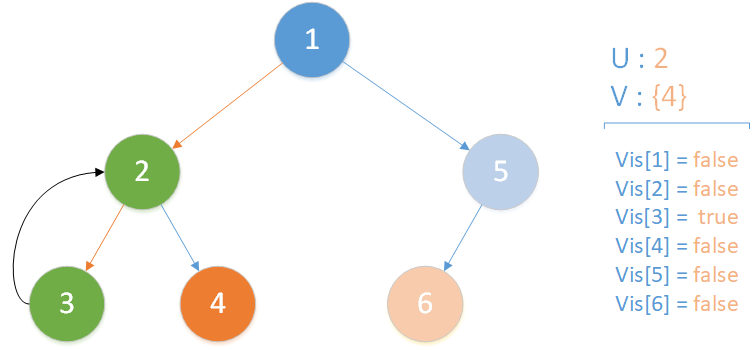
递归返回,当前所在位置 u = 2 ,合并节点 3 到 u 所在集合,标记 vis[3] = true ,此时未遍历孩子集合 v = {4} ,向下遍历。
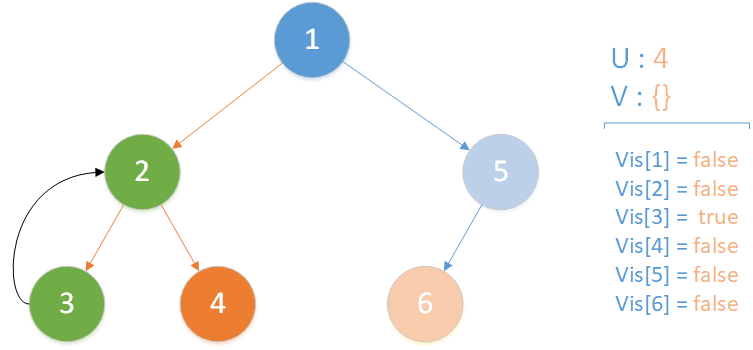
当前所在位置 u = 4 ,未遍历孩子集合 v = {} ,遍历所有相关查询发现存在 LCA(T,3,4) ,且 vis[3] = true ,此时得到该查询的解为节点 3 所在集合的首领,即 LCA(T,3,4) = 2 ;又发现存在相关查询 LCA(T,4,6) ,但是节点 6 此时标记未访问,因此什么也不做。该层递归结束。
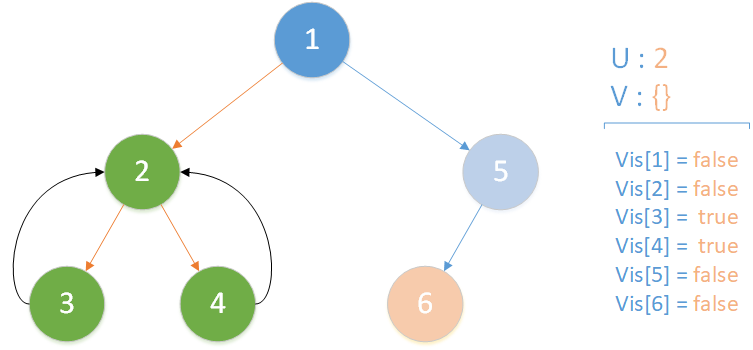
递归返回,当前所在位置 u = 2 ,合并节点 4 到 u 所在集合,标记 vis[4] = true ,未遍历孩子集合 v = {} ,遍历相关查询发现存在 LCA(T,2,1) ,但是节点 1 此时标记未访问,因此什么也不做,该层递归结束。
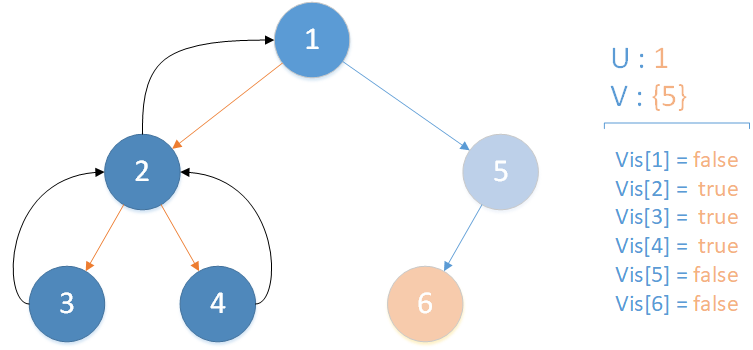
递归返回,当前所在位置 u = 1 ,合并节点 2 到 u 所在集合,标记 vis[2] = true ,未遍历孩子集合 v = {5} ,继续向下遍历。
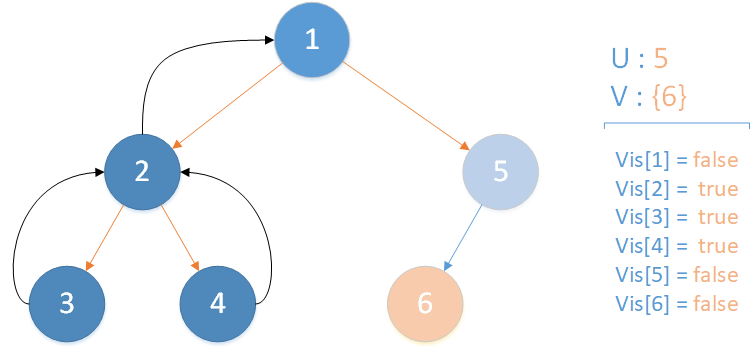
当前所在位置 u = 5 ,未遍历孩子集合 v = {6} ,继续向下遍历。
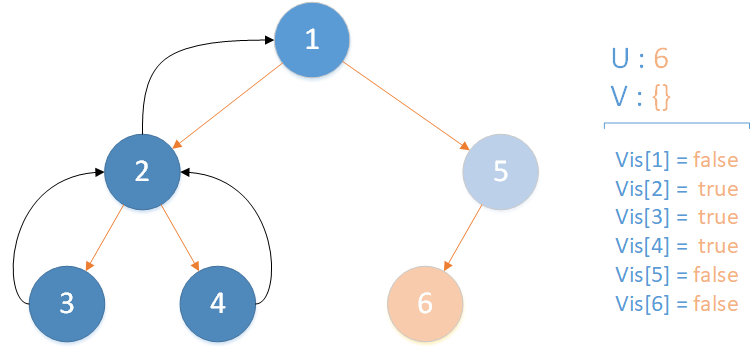
当前所在位置 u = 6 ,未遍历孩子集合 v = {} ,遍历相关查询发现存在 LCA(T,4,6) ,且 vis[4] = true ,因此得到该查询的解为节点 4 所在集合的首领,即 LCA(T,4,6) = 1 ,该层递归结束。
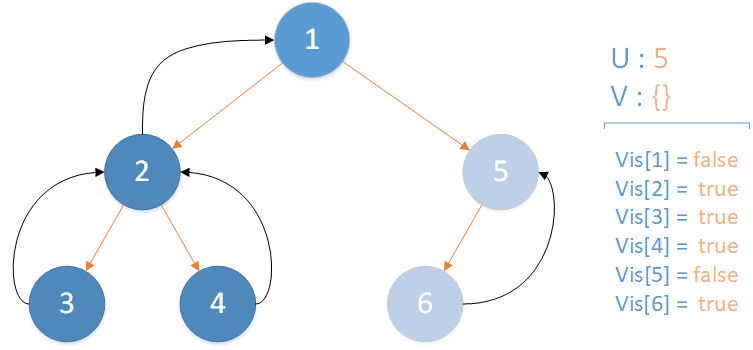
递归返回,当前所在位置 u = 5 ,合并节点 6 到 u 所在集合,并标记 vis[6] = true ,未遍历孩子集合 v = {} ,无相关查询因此该层递归结束。
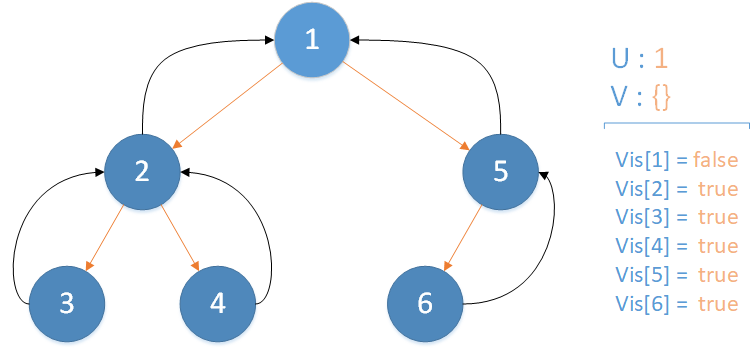
递归返回,当前所在位置 u = 1 ,合并节点 5 到 u 所在集合,并标记 vis[5] = true ,未遍历孩子集合 v = {} ,遍历相关查询发现存在 LCA(T,2,1) ,此时该查询的解便是节点 2 所在集合的首领,即 LCA(T,2,1) = 1 ,递归结束。
至此整个 Tarjan 算法便结束啦~
PS:不要在意最终根节点的颜色和其他节点颜色有一点点小小差距,可能是千千在染色的时候没仔细看,总之就这样咯~
PPS:所谓的首领就是、就是首领啦~




 浙公网安备 33010602011771号
浙公网安备 33010602011771号