最小生成树（Kruskal和Prim算法）
关于图的几个概念定义：
关于图的几个概念定义：
- 连通图：在无向图中，若任意两个顶点vi与vj都有路径相通，则称该无向图为连通图。
- 强连通图：在有向图中，若任意两个顶点vi与vj都有路径相通，则称该有向图为强连通图。
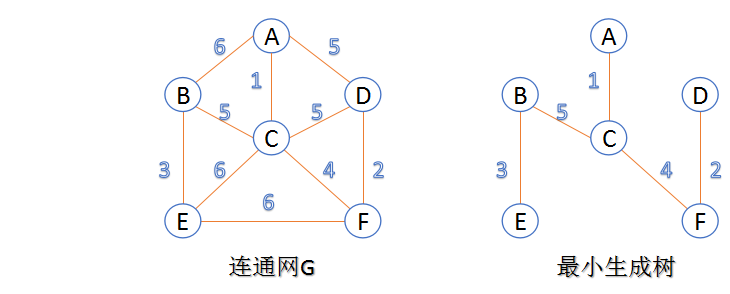
- 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
- 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
- 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。
构造最小生成树的准则有3条：
（1）必须只使用该网络中的边来构造最小生成树。
（2）必须使用且仅使用n-1条边来连接网络中的n个顶点。
（3）不能使用产生回路的边。
下面介绍两种求最小生成树算法
1 Prim（普利姆算法）算法--加点法
此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。
Prim算法从任意一个顶点开始，每次选择一个与当前顶点集最近的一个顶点，并将两顶点之间的边加入到树中。Prim算法在找当前最近顶点时使用到了贪婪算法。
| 图例 | 说明 | 不可选 | 可选 | 已选（Vnew） |
|---|---|---|---|---|
|
|
此为原始的加权连通图。每条边一侧的数字代表其权值。 | - | - | - |
|
|
顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。 | C, G | A, B, E, F | D |
|
|
下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。 | C, G | B, E, F | A, D |
 |
算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。 | C | B, E, G | A, D, F |
|
|
在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。 | 无 | C, E, G | A, D, F, B |
|
|
这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。 | 无 | C, G | A, D, F, B, E |
|
|
顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。 | 无 | G | A, D, F, B, E, C |
|
|
现在，所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。 | 无 | 无 | A, D, F, B, E, C, G |
1 #include<stdio.h> 2 #include<string.h> 3 #define MAX 0x3f3f3f3f 4 using namespace std; 5 int logo[1010];///用0和1来表示是否被选择过 6 int map1[1010][1010]; 7 int dis[1010];///记录任意一点到这一点的最近的距离 8 int n,m; 9 int prim() 10 { 11 int i,j,now; 12 int sum=0; 13 for(i=1;i<=n;i++)///初始化 14 { 15 dis[i]=MAX; 16 logo[i]=0; 17 } 18 for(i=1;i<=n;i++) 19 { 20 dis[i]=map1[1][i]; 21 } 22 dis[1]=0; 23 logo[1]=1; 24 for(i=1;i<n;i++)///循环查找 25 { 26 now=MAX; 27 int min1=MAX; 28 for(j=1;j<=n;j++) 29 { 30 if(logo[j]==0&&dis[j]<min1) 31 { 32 now=j; 33 min1=dis[j]; 34 } 35 } 36 if(now==MAX)///防止不成图 37 { 38 break; 39 } 40 logo[now]=1; 41 sum=sum+min1; 42 for(j=1;j<=n;j++)///填入新点后更新最小距离，到顶点集的距离 43 { 44 if(logo[j]==0&&dis[j]>map1[now][j]) 45 { 46 dis[j]=map1[now][j]; 47 } 48 } 49 } 50 if(i<n) 51 { 52 printf("?\n"); 53 } 54 else 55 { 56 printf("%d\n",sum); 57 } 58 } 59 int main() 60 { 61 while(scanf("%d%d",&m,&n)!=EOF)///n是点数 62 { 63 if(m==0) 64 { 65 break; 66 } 67 memset(map1,0x3f3f3f3f,sizeof(map1));///map是邻接矩阵储存图的信息 68 for(int i=0;i<m;i++) 69 { 70 int a,b,c; 71 scanf("%d%d%d",&a,&b,&c); 72 if(c<map1[a][b])///防止出现重边 73 { 74 map1[a][b]=map1[b][a]=c; 75 } 76 } 77 prim(); 78 } 79 return 0; 80 }
邻接表实现：
1 #include<stdio.h> 2 #include<string.h> 3 #include<vector> 4 #include<algorithm> 5 #define INF 0x3f3f3f3f 6 using namespace std; 7 struct node 8 { 9 int end;///终点 10 int power;///权值 11 } t; 12 int n;///n为点数 13 vector<node>q[500001];///邻接表储存图的信息 14 int dis[500001];///距离 15 int vis[500001];///标记数组 16 void prime() 17 { 18 int i,len,j,pos,sum,start; 19 memset(vis,0,sizeof(vis)); 20 sum=0; 21 start=1;///任意取起点 22 for(i=0; i<=n; i++) 23 { 24 dis[i]=INF; 25 } 26 len=q[start].size(); 27 for(i=0; i<len; i++)///从任意起点开始的dis数组更新 28 { 29 if(q[start][i].power<dis[q[start][i].end]) 30 { 31 dis[q[start][i].end]=q[start][i].power; 32 } 33 } 34 vis[start]=1; 35 for(j=0; j<n-1; j++) 36 { 37 int pos,min=INF; 38 for(i=1; i<=n; i++) 39 { 40 if(vis[i]!=0&&dis[i]<min) 41 { 42 min=dis[i]; 43 pos=i;///找到未访问节点中权值最小的 44 } 45 } 46 if(pos==INF)///防止不成图 47 { 48 break; 49 } 50 vis[pos]=1; 51 sum=sum+min; 52 len=q[pos].size();///再次更新dis数组 53 for(j=0; j<len; j++) 54 { 55 if(vis[q[pos][j].end]==0&&dis[q[pos][j].end]>q[pos][j].power) 56 { 57 dis[q[pos][j].end] = q[pos][j].power; 58 } 59 } 60 } 61 if(j<n) 62 { 63 printf("?\n"); 64 } 65 else 66 { 67 printf("%d\n",sum); 68 } 69 } 70 int main() 71 { 72 int m,i; 73 int begin,end,power; 74 int a,b; 75 while(scanf("%d%d",&n,&m)!=EOF) 76 { 77 for(i=0; i<=n; i++) 78 { 79 q[i].clear();///将victor数组清空 80 } 81 for(i=0; i<m; i++) 82 { 83 scanf("%d%d%d",&begin,&end,&power);///输入 84 t.end=end; 85 t.power=power; 86 q[begin].push_back(t); 87 t.end=begin;///无向图 88 t.power=power; 89 q[end].push_back(t); 90 } 91 prime(); 92 } 93 return 0; 94 }
这里再给出一个没有使用标记数组的代码：
int prim(int s) { int i,j,sum=0; int now; for(i=1;i<=n;i++) { closest[i]=INT_MAX; } for(i=1;i<=n;i++) { closest[i]=map[s][i]; } closest[s]=0; for(i=1;i<n;i++)//这里的i代表的是边数，有n个点就会有n-1条边 { int min=INT_MAX; for(j=1;j<=n;j++) { if(closest[j]&&closest[j]<min) { min=closest[j]; now=j;//找到所需的最小边 } } sum+=min; closest[now]=0;//将找到的边加入到最小生成树之中 for(j=1;j<=n;j++)//找到新的点加入已选点集合之后，更新该点到未选点集合的距离 { if(map[now][j]&&map[now][j]<closest[j]) { closest[j]=map[now][j]; } } } return sum; }
2 Kruskal（克鲁斯卡尔）算法--加边法
1.概览
Kruskal算法是一种用来寻找最小生成树的算法，在剩下的所有未选取的边中，找最小边，如果和已选取的边构成回路，则放弃，选取次小边。
2.实现过程
1).记Graph中有v个顶点，e个边
2).新建图Graphnew，Graphnew中拥有原图中相同的e个顶点，但没有边
3).将原图Graph中所有e个边按权值从小到大排序
4).循环：从权值最小的边开始遍历每条边 直至图Graph中所有的节点都在同一个连通分量中 if 这条边连接的两个节点于图Graphnew中不在同一个连通分量中 添加这条边到图Graphnew中
图例描述：
首先第一步，我们有一张图Graph，有若干点和边
将所有的边的长度排序，用排序的结果作为我们选择边的依据。这里再次体现了贪心算法的思想。资源排序，对局部最优的资源进行选择，排序完成后，我们率先选择了边AD。这样我们的图就变成了下图
在剩下的变中寻找。我们找到了CE。这里边的权重也是5
依次类推我们找到了6,7,7，即DF，AB，BE。
下面继续选择， BC或者EF尽管现在长度为8的边是最小的未选择的边。但是现在他们已经连通了（对于BC可以通过CE,EB来连接，类似的EF可以通过EB,BA,AD,DF来接连）。所以不需要选择他们。类似的BD也已经连通了（这里上图的连通线用红色表示了）。最后就剩下EG和FG了。当然我们选择了EG。
代码：（利用并查集来实现）
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; int n,m,sum; struct node { int start;///起点 int end;///终点 int power;///权值 }edge[5050]; int pre[5050]; int cmp(node a,node b) { return a.power<b.power;///按权值排序 } int Find(int x)///并查集找祖先 { if(x!=pre[x])///递归法 { pre[x]=Find(pre[x]); } return pre[x]; /*int a;///循环法 a=x; while(pre[a]!=a) { a=pre[a]; } return a;*/ } void Union(int x,int y,int n) { int fx =Find(x); int fy =Find(y); if(fx!=fy) { pre[fx]=fy; sum+=edge[n].power; } } int main() { int i; while(scanf("%d",&n)!=EOF) { sum=0; m=n*(n-1)/2; for(i=1;i<=m;i++) { scanf("%d%d%d",&edge[i].start,&edge[i].end,&edge[i].power); } for(i=1;i<=m;i++)///并查集的初始化 { pre[i]=i; } sort(edge+1,edge+m+1,cmp); for(i=1;i<=m;i++) { Union(edge[i].start,edge[i].end,i); } printf("%d\n",sum); } return 0; }
