传教士和野人过河（经典MC问题）

     这个问题本来是《人工智能技术导论》第三章的课后题，今天上午考试正巧考到了这道题，要我们画状态转换图，我之前思考过一点，所以写出的状态表示应该没有问题，但这些状态太多了.......,十来种状态直接给我干懵逼了，两个小时的考试，差不多得有一个小时在推导状态转换关系，最后整个考场就剩下我和谭神两个人了，这里写下博客，整理一下这个问题。

网上搜索发现这个博主的做法和我的做法大致一样的，他最后给出了C++的实现方式。这篇博客状态分析部分就主要参考https://www.cnblogs.com/guanghe/p/5485800.html

后面再附上PROLOG程序的解决方案。

一、问题重述  

在河的左岸有N个传教士、N个野人和一条船，传教士们想用这条船把所有人都运过河去，但有以下条件限制：

（1）修道士和野人都会划船，但船每次最多只能运K个人；
（2）在任何岸边野人数目都不能超过修道士，否则修道士会被野人吃掉。

假定野人会服从任何一种过河安排，请规划出一个确保修道士安全过河的计划。

二、问题分析 

1、约束条件

  ① M≧C 任何时刻两岸、船上都必须满足传教士人数不少于野人数（M=0时除外，既没有传教士） 
  ② M+C≦K 船上人数限制在K以内

2、求解 

 传教士与野人全部安全渡到对岸的解决方案

三、状态表示

    设N=3，K=2（三个M和三个C，每次渡河二人以下）     
     L：左岸，R：右岸， 
     B：是否有船（0：无船，1：有船） 

    定义：用三元组（ML，CL，BL）表示左岸状态，其中：
    0≦ML,CL≦3，BL∈｛0,1｝
    如：（0，3，1）表示左岸有三个野人，船在左岸。
    从（3，3，1）到（0，0，0）的状态转换
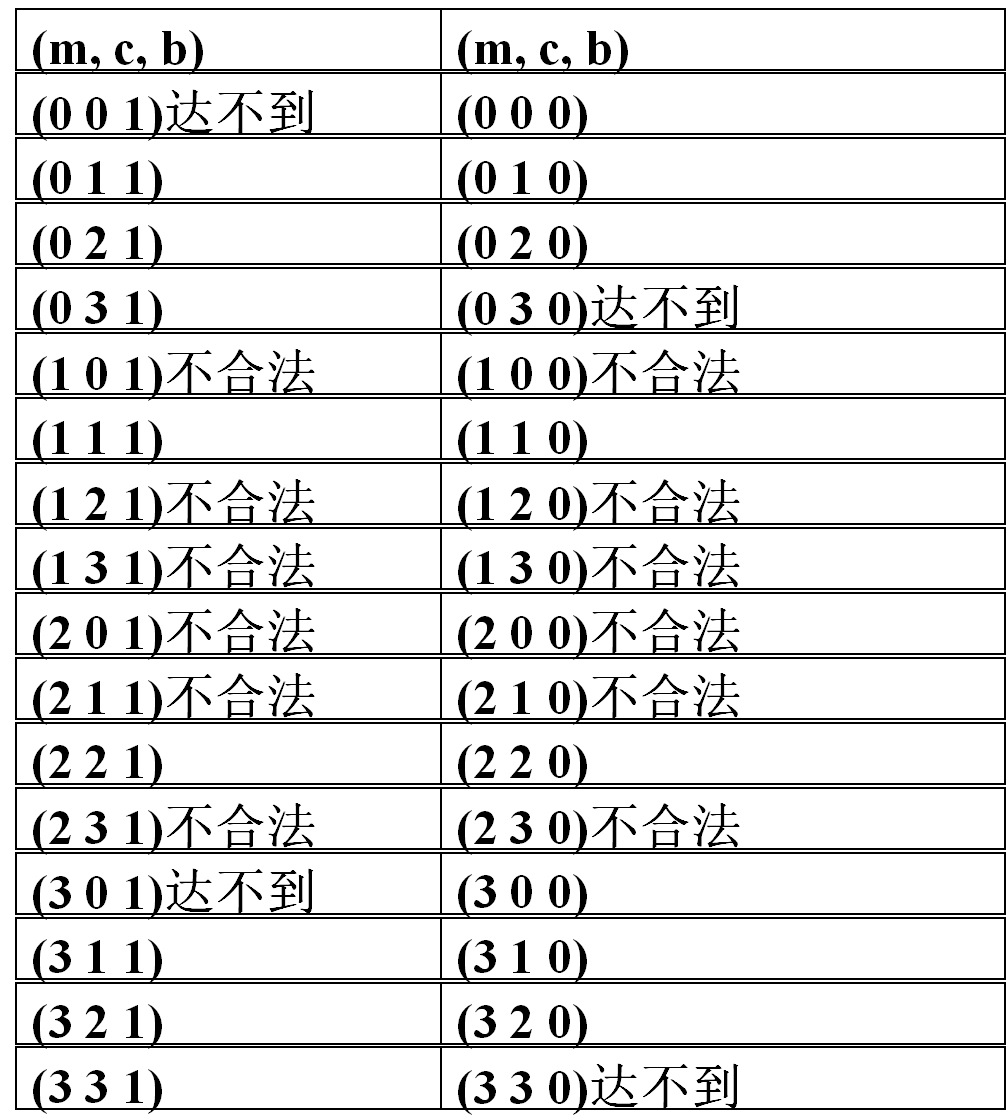
    状态空间：32 种状态，其中：
    12种不合理状态：如（1，0，1）说明右岸有2个M，3个C；
    4种不可能状态：如（3，3，0）说明所有M和C都在左岸，而船在右岸
   

 ∴可用的状态共16种，组成合理的状态空间 
    

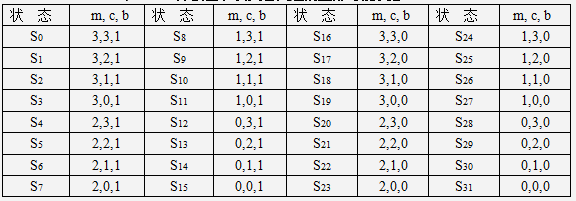
        状态空间具体描述
       

四、操作集

    定义：Pmc操作：从左岸划向右岸

               Qmc操作：从右岸划向左岸

 船上人数组合（m，c）共5种（1，0）,（1，1）,（2，0）,（0，1）,（0，2）

    ∵每一种船上的人数组合同时对应P，Q二种操作

    ∴系统共有5×2＝10种操作（规则）

 如：P10：if （ML，CL，BL=1） then （ML-1，CL，BL-1）

     如果船在左岸，那么一个传教士划船到右岸

     Q01：if （ML，CL，BL=0） then （ML，CL+1，BL+1）

     如果船在右岸，那么一个野人划船回到左岸

 总共有10种操作

  F={P10,P20, P11, P01, P02, Q 10, Q 20, Q 11, Q 01, Q 02} 
  P₁₀   if( ML ,CL , BL=1 )   then ( ML–1 , CL , BL–1 )
  P₀₁   if( ML ,CL , BL=1 )   then ( ML , CL–1 , BL–1 )
  P₁₁   if( ML ,CL , BL=1 )   then ( ML–1 , CL–1 ,BL –1 )
  P₂₀   if( ML ,CL , BL=1 )   then ( ML–2 , CL , BL–1 )
  P₀₂   if( ML ,CL , BL=1 )   then ( ML , CL–2 , BL–1 )
  Q₁₀   if( ML ,CL , BL=0 )   then ( ML+1 , CL ,BL+1 )
  Q₀₁   if( ML ,CL , BL=0 )   then ( ML , CL+1 , BL+1 )
  Q₁₁   if( ML ,CL , BL=0 )   then ( ML+1 , CL +1,BL +1 )
  Q₂₀   if( ML ,CL , BL=0 )   then ( ML+2 , CL +2,BL +1 ) 
  Q₀₂   if( ML ,CL , BL=0 )   then ( ML , CL +2, BL+1 ) 

控制策略
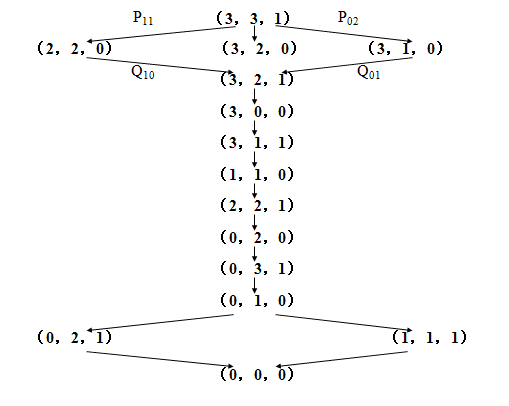
    最短路径有4条，由11次操作构成。

(P11、Q10、P02、Q01、P20、Q11、P20、Q01、P02、Q01、P02)
(P11、Q10、P02、Q01、P20、Q11、P20、Q01、P02、Q10、P11)
(P02、Q01、P02、Q01、P20、Q11、P20、Q01、P02、Q01、P02) 
(P02、Q01、P02、Q01、P20、Q11、P20、Q01、P02、Q10、P11)  

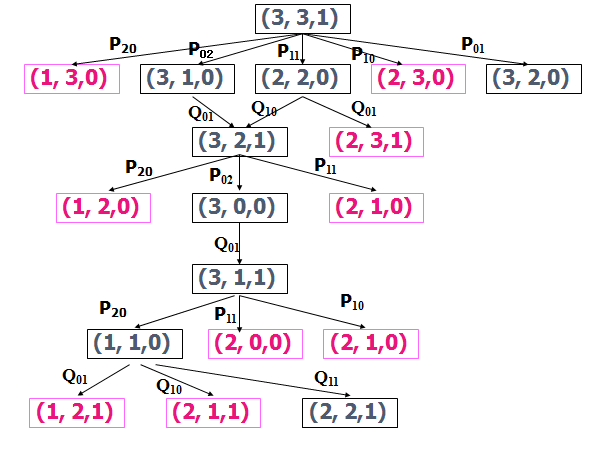
五、状态空间图

     状态空间图是一个有向图，图中的节点代表状态，节点之间的连线代表操作，箭头代表状态的转换方向。
 

六、PROLOG程序设计

这里给出参考的链接https://github.com/kylynf/PrologMC

% start([3,3,near]).
% goal([0,0,far]).

change(near,far).
change(far,near).

% boat must be in valid location
% valid number of missionaries and cannibals on each shore
% no more than three and no fewer than zero
valid([Missionaries,Cannibals,near]) :-
    Missionaries=<3,
    Cannibals=<3,
    Missionaries>=0,
    Cannibals>=0.

valid([Missionaries,Cannibals,far]) :-
    Missionaries=<3,
    Cannibals=<3,
    Missionaries>=0,
    Cannibals>=0.

% oneEq(X,X,_).
% oneEq(X,_,X).

% no missionaries are in danger of being eaten
safe([Missionaries,Cannibals,_]) :-
    % oneEq(3,3,_),oneEq(2,2,_),oneEq(1,1,_),oneEq(0,0,_),oneEq(0,1,_),oneEq(0,2,_),oneEq(0,3,_),oneEq(3,0,_),oneEq(3,1,_),oneEq(3,2,_).
    % (Missionaries=<Cannibals ; Cannibals=0),
    (Missionaries>=Cannibals ; Missionaries=0),
    FarMis is 3 - Missionaries, FarCan is 3 - Cannibals,
    (FarMis >= FarCan; FarMis=0).

% onemissionary
move([M1,C1,B1],onemissionary,[M2,C2,B2]) :-
    change(B1, B2),
    C1 = C2,
    (B1=near -> DM is M1-1 ; DM is M1+1),
    M2 = DM.

%twomissionaries
move([Missionaries1,Cannibals1,Boat1],twomissionaries,[Missionaries2,Cannibals2,Boat2]) :-
    change(Boat1,Boat2),
    Cannibals1 = Cannibals2,
    (Boat1=near -> DummyMissionary is Missionaries1-2 ; DummyMissionary is Missionaries1+2),
    Missionaries2 = DummyMissionary.

%onecannibal
move([Missionaries1,Cannibals1,Boat1],onecannibal,[Missionaries2,Cannibals2,Boat2]) :-
    % boat1==near,boat2==far,Cannibals2 is Cannibals1 - 1;
    % boat1==far,boat2==near,Cannibals2 is Cannibals1 + 1.
    change(Boat1,Boat2),
    Missionaries1 = Missionaries2,
    (Boat1=near -> DummyCannibal is Cannibals1-1 ; DummyCannibal is Cannibals1+1),
    Cannibals2 = DummyCannibal.

%twocannibal
move([Missionaries1,Cannibals1,Boat1],twocannibals,[Missionaries2,Cannibals2,Boat2]) :-
    change(Boat1, Boat2),
    Missionaries1 = Missionaries2,
    (Boat1=near -> DummyCannibal is Cannibals1-2 ; DummyCannibal is Cannibals1+2),
    Cannibals2 = DummyCannibal.

% oneofeach
move([Missionaries1,Cannibals1,Boat1],oneofeach,[Missionaries2,Cannibals2,Boat2]) :-
    change(Boat1,Boat2),
    (Boat1=near -> DummyCannibal is Cannibals1-1, DummyMissionary is Missionaries1-1 ; DummyCannibal is Cannibals1+1, DummyMissionary is Missionaries1+1),
    Cannibals2 = DummyCannibal,
    Missionaries2 = DummyMissionary.

solution([0,0,far],[]).
solution(State,[Move|Rest]) :-
    move(State,Move,NextState),
    valid(NextState),
    safe(NextState),
    solution(NextState,Rest).

solve(X) :-
    length(X,11),
    solution([3,3,near],X).