算法设计与分析——n后问题(回溯法+位运算)
一、问题描述
在n×n格的国际象棋上摆放n个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。

二、算法设计


解n后问题的回溯算法描述如下:
#include <iostream> #include <cstdio> #include <cmath> #include <algorithm> using namespace std; int n; long long int sum; int x[11]; int Check(int row, int col) { for(int i = 1; i < row; i++) { if(col == x[i] || abs(row - i) ==abs(col - x[i])) //在同一列或者在同一斜线。一定不在同一行 return 0; } return 1; } void backtrack(int k) { if(k>n) //求出一种解, sum+1 { sum++; return; } for(int i=1; i<=n; i++)//n叉树 { if(Check(k, i)) //剪枝,检查是否满足条件 { x[k]=i; //记录第k皇后在第i列 backtrack(k+1); //递归查找 } } } int main() { while(scanf("%d",&n)!=EOF) { if(n==0) { break; } for(int i=0; i<n; i++) { x[i]=0; } sum=0; backtrack(1); printf("%lld\n",sum); } return 0; }
三、位运算优化
上面的程序我在求16皇后的时候大概跑了近乎200s,我们可以想象到每次搜索第k行的状态的时候,都是从第1列开始枚举每一列,这样是很低效的,浪费了很多时间,我们需要提高枚举的命中率甚至每一次的尝试都是正确的,都是可行解。
那么该怎么做?
其实n皇后的搜索规模并不是很大,在目前的需求中,最多不过20位,我们可以使用二进制来表示一个集合,而一旦使用二进制时,集合的交并补运算就可以直接使用位运算来实现了,我们知道位运算在计算机中是相当快的(使用指令少)。安利一篇我之前做过的位运算的实验https://www.cnblogs.com/wkfvawl/p/10034576.html
两个数字与运算就是求交集,或运算就是求并集,取反就是求集合的补集。
我们先来看程序代码:
void test(int row, int ld, int rd) { int pos, p; if ( row != upperlim ) { pos = upperlim & (~(row | ld | rd )); while ( pos ) { p = pos & (~pos + 1); pos = pos - p; test(row | p, (ld | p) << 1, (rd | p) >> 1); } } else ++Ans; }
初始化:
upperlim = (1 << n)-1; Ans = 0;
upperlime =(1 << n)-1 就生成了n个1组成的二进制数。
程序从上到下搜索。
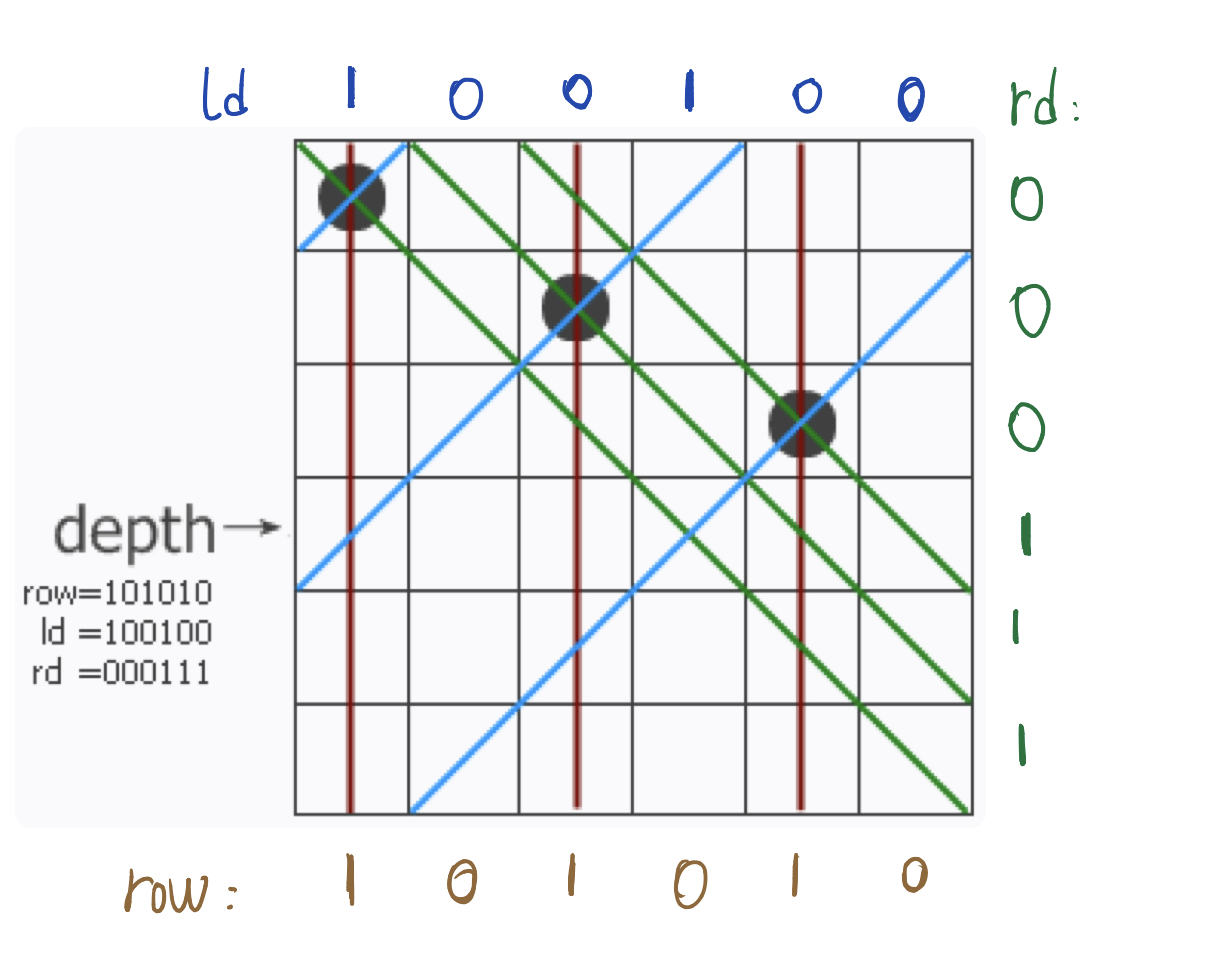
这样我们使用三个参数row、ld和rd,分别表示在纵列和两个对角线方向的限制条件下这一行的哪些地方不能放。位于该行上的不能放置的位置就用row、ld和rd中的1来表示。把它们三个并起来,得到该行所有的禁位,取反后就得到所有可以放的位置(用pos来表示)
这里需要注意一点:
对应row、ld和rd来说1表示的是不能放置皇后的占用位置,但对于pos来说1代表可以放置皇后的位置!
p = pos & (~pos + 1)其结果是取出最右边的那个1。
因为取反以后刚好所有数都是相反,再加 1 ,就是改变最低位,如果低位的几个数都是1,加的这个 1 就会进上去,一直进到 0 ,在做与运算就和原数对应的 1 重合了。举例可以说明:
原数 0 0 0 0 1 0 0 0 原数 0 1 0 1 0 0 1 1
取反 1 1 1 1 0 1 1 1 取反 1 0 1 0 1 1 0 0
加1 1 1 1 1 1 0 0 0 加1 1 0 1 0 1 1 0 1
与运算 0 0 0 0 1 0 0 0 and 0 0 0 0 0 0 0 1
从集合的角度来看p是位置集合pos上的一位置,将皇后置于位置p,位置集合就要减少一个位置,所以需要:
pos = pos - p
那这个while我们也就明白了,需要把位置集合全都用完放置皇后嘛!
最后我们要注意递归调用时三个参数的变化,每个参数都加上了一个占位,但两个对角线方向的占位对下一行的影响需要平移一位。最后,如果递归到某个时候发现row=upperlim了,说明n个皇后全放进去了,找到的解的个数加1。
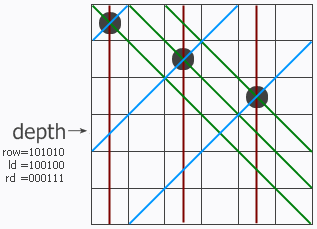
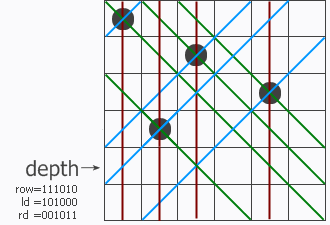
这里拿两个例子来说明,对于第一张图的例子。
在已经安置好3个皇后的情况下,对于第4个皇后
row = 101010 棕色线代表纵列上不能放置皇后的占位
ld = 100100 蓝色线代表左对角线列上不能放置皇后的占位
rd = 000111 绿色线代表右对角线列上不能放置皇后的占位
对角线是45度倾斜的,这样两个对角线方向的占位要影响下一行对应位置的下一位也就很好理解了,这恰恰可以使用位运算的左移和右移来实现。
(ld | p)<< 1 是因为由ld造成的占位在下一行要右移一下;
(rd | p)>> 1 是因为由rd造成的占位在下一行要左移一下。
当然 ld rd row 还要和upperlime 与运算 一下,这样做的结果就是从最低位数起取n个数为有效位置,原因是在上一次的运算中ld发生了右移,如果不and的话,就会误把n以外的位置当做有效位。
#include<cstdio> #include<algorithm> #define ll long long int using namespace std; // sum用来记录皇后放置成功的不同布局数;upperlim用来标记所有列都已经放置好了皇后。 ll sum; ll upperlim = 1; // 试探算法从最右边的列开始。 void test(ll row, ll ld, ll rd) { if (row != upperlim) { // row,ld,rd进行“或”运算,求得所有可以放置皇后的列,对应位为0, // 然后再取反后“与”上全1的数,来求得当前所有可以放置皇后的位置,对应列改为1 // 也就是求取当前哪些列可以放置皇后 ll pos = upperlim & ~(row | ld | rd); while (pos) // 0 -- 皇后没有地方可放,回溯 { // 拷贝pos最右边为1的bit,其余bit置0 // 也就是取得可以放皇后的最右边的列 ll p = pos&-pos; // 将pos最右边为1的bit清零 // 也就是为获取下一次的最右可用列使用做准备, // 程序将来会回溯到这个位置继续试探 pos -= p; // row + p,将当前列置1,表示记录这次皇后放置的列。 // (ld + p) << 1,标记当前皇后左边相邻的列不允许下一个皇后放置。 // (ld + p) >> 1,标记当前皇后右边相邻的列不允许下一个皇后放置。 // 此处的移位操作实际上是记录对角线上的限制,只是因为问题都化归 // 到一行网格上来解决,所以表示为列的限制就可以了。显然,随着移位 // 在每次选择列之前进行,原来N×N网格中某个已放置的皇后针对其对角线 // 上产生的限制都被记录下来了 test(row + p, (ld + p) << 1, (rd + p) >> 1); } } else { // row的所有位都为1,即找到了一个成功的布局,回溯 sum++; } } int main() { int n; while(scanf("%d",&n)!=EOF) { if(n==0) { break; } sum = 0; upperlim = (1 << n) - 1; test(0,0,0); printf("%lld\n",sum); } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号