FFM算法解析及Python实现

1. 什么是FFM？

通过引入field的概念，FFM把相同性质的特征归于同一个field，相当于把FM中已经细分的feature再次进行拆分从而进行特征组合的二分类模型。

2. 为什么需要FFM？

在传统的线性模型中，每个特征都是独立的，如果需要考虑特征与特征之间的相互作用，可能需要人工对特征进行交叉组合。非线性SVM可以对特征进行核变换，但是在特征高度稀疏的情况下，并不能很好的进行学习。由于推荐系统是一个高度系数的数据场景，由此产生了FM系列算法，包括FM，FFM，DeepFM等算法。

3. FFM用在哪？

和FM算法一样，FFM主要应用在推荐算法中的CTR点击率预估（排序）问题，推荐系统一般可以分成两个模块，召回和排序。比如对于电影推荐，召回模块会针对用户生成一个推荐电影列表，而排序模块则负责对这个电影列表根据用户的兴趣做排序。当把FFM算法应用到推荐系统中时，具体地是应用在排序模块。

4. FFM长什么样？

FFM模型结构

线性部分大家都很熟悉，非线性部分是FFM的关键所在，并且与同样有非线性部分的FM算法相比，FFM引入了field的概念。因此交叉项与FM算法的<vi , vj>不同，这里的是<vi,fj , vj,fi>

5. FFM交叉项的计算

以下图网上流传广泛的图为例：

其中，红色部分对应的是Field，来自于原始特征的个数；
蓝色部分对应的是feature，来自于原始特征onehot之后的个数。(连续型特征不用one-hot)
对于特征Feature:User=YuChin，有Movie=3Idiots、Genre=Comedy、Genre=Drama、Price四项要进行交叉组合：

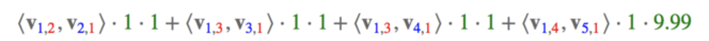
绿色部分为对应特征one-hot之后的值，出现为1，不出现为0。对于连续型变量的处理，这里采用的是使用实际值，当然，也可以对连续型变量离散化处理，再进行one-hot。

6. FFM代码分析

这里我们的FFM算法是基于Tensorflow实现的。

为什么用Tensorflow呢？观察二次项，由于field的引入，Vffm需要计算的参数有 nfk 个，远多于FM模型的 nk个，而且由于每次计算都依赖于乘以的xj的field，所以，无法用fm的计算技巧(ab = 1/2(a+b)^2-a^2-b^2)，所以计算复杂度是 O(n^2)。

因此使用Tensorflow的目的是想通过GPU进行计算。同时这也给我们提供了一个思路：如果模型的计算复杂度较高，当不能使用CPU快速完成模型训练时，可以考虑使用GPU计算。比如Xgboost是已经封装好可以用在GPU上的算法库，而那些没有GPU版本的封装算法库时，例如我们此次采用的FFM算法，我们可以借助Tensorflow的GPU版本框架设计算法，并完成模型训练。

代码主要分三部分：

build_data.py

主要是完成对原始数据的转化。主要包括构造特征值对应field的字典。

FFM.py

主要包括线性部分及非线性部分的代码实现。

tools.py

主要包括训练集的构造。

这里我们主要分析 FFM.py，也就是模型的构建过程：

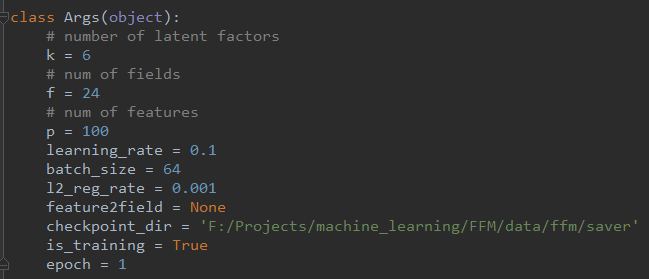
首先初始化一些参数，包括：

  • k：隐向量长度
  • f ：field个数
  • p：特征值个数
  • 学习率大小
  • 批训练大小
  • 正则化
  • 模型保存位置等

代码如下图所示：

 

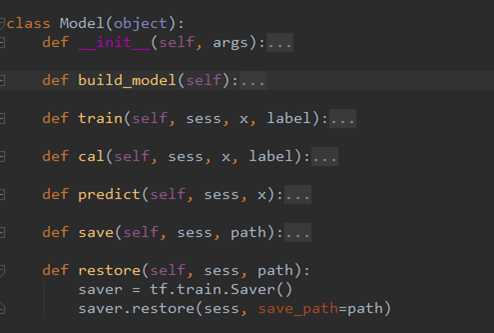
然后，构造了一个model类，主要存放：

  • 初始化的一些参数
  • 模型结构
  • 模型训练op（参数更新）
  • 预测op
  • 模型保存以及载入的op

代码如下图所示：

 

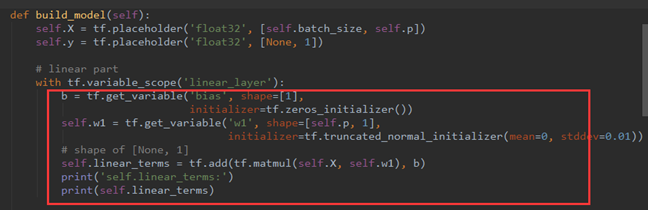
之后，对模型构造部分代码进行分析，可发现模型由两部分组成，第一部分是下图红框内容，其实就是线性表达式 w^Tx+b，其中：

  • b shape(None,1)
  • x shape (batch_size,p)
  • w1 shape(p,1)    注：p为特征值个数

定义变量及初始化后，就可以构造线性模型，代码如下图所示：

 

 

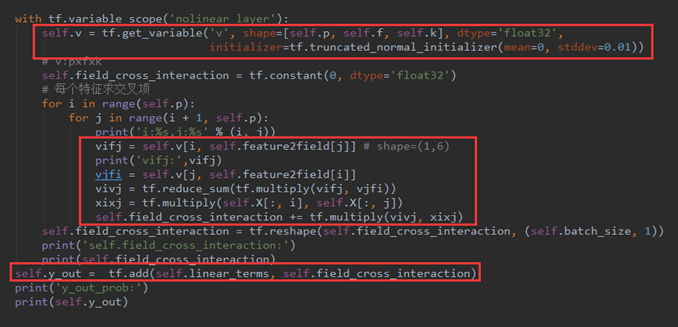
然后，定义一个Vffm变量用来存放交叉项的权重，并初始化。因为我们已经了解到Vffm是一个三维向量，所以，v ：shape(p,f,k) 。

之后是vi,fj、vj,fi的构造。因为v 有p行，代表共有p个特征值，所以vifj = v[i, feature2field[j]]，说人话就是第i个特征值在第j个特征值对应的field上的隐向量。

vjfi 的构造方法类似，所以vivj就可以求出来.然后就是把交叉项累加，然后 reshape 成（batch_size，1）的形状，以便与线性模型进行矩阵加法计算。

代码如下图所示：

  

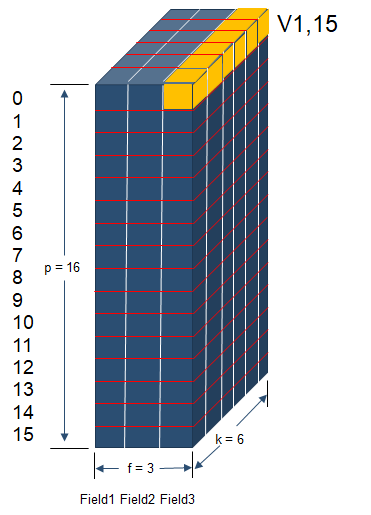
下图描述了所有交叉项的隐向量Vffm所处的位置。假设p=16、f=3、k=6，16个项所属的field为{0: 0, 1: 0, 2: 0, 3: 0, 4: 0, 5: 0, 6: 1, 7: 1, 8: 1, 9: 1, 10: 2, 11: 2, 12: 2, 13: 2, 14: 2, 15: 2}，共有120个交叉项，vifj和vjfi隐向量分别各有120个。其中：

vifj隐向量： {(3, 0), (11, 2), (2, 1), (6, 2), (5, 1), (7, 2), (4, 0), (1, 2), (12, 2), (8, 1), (2, 2), (4, 1), (1, 1), (3, 2), (0, 0), (13, 2), (8, 2), (7, 1), (4, 2), (1, 0), (14, 2), (0, 1), (9, 2), (6, 1), (3, 1), (2, 0), (5, 2), (0, 2), (10, 2)}，共29个不同的隐向量。
vjfi隐向量： {(12, 1), (9, 1), (3, 0), (11, 2), (8, 0), (15, 1), (14, 0), (4, 0), (12, 2), (9, 0), (8, 1), (15, 0), (14, 1), (11, 1), (5, 0), (10, 0), (13, 2), (7, 1), (6, 0), (11, 0), (10, 1), (1, 0), (14, 2), (13, 1), (7, 0), (15, 2), (12, 0), (2, 0), (13, 0)}，共29个不同的隐向量。

而vifj和vjfi相加起来共有48个各不相同的隐向量。也就是说，下图展示的每一个隐向量都有用，即都能在模型中找到，且很多交叉项的隐向量一样。

举个栗子：

v1,15代表着第1个特征值在第15个特征值对应的field（field=2）上的隐向量。即v1,15 = v[1, feature2field[15]] = Vffm[1,2] ，其中v1,15的shape = (1,6)。

 

最后，就是loss的定义。这里要注意我们之前在构造训练集时已经把输出的（0，1）分类转化为（-1，1）分类。

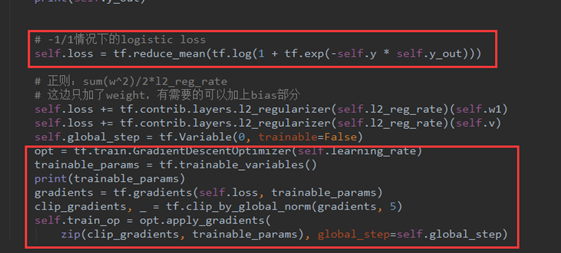
核心加重点是关注loss的计算公式，此时的计算公式是-1/1做二分类的时候常用的loss计算方法。

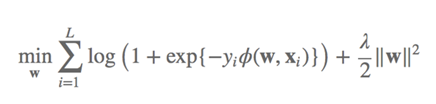
7.  总结

7.1 FFM 算法流程

7.1.1 输入部分

  1. 类别型特征对应的变量的值映射为0到n-1

  2. 连续型变量保持原样，不做处理，只需把变量名映射为n即可。（也可按实际情况进行离散化处理）

  3. 根据每一特征所属的field，构造字典：每一field的取值，例如：field为0，那么{0：0，0：1，0：2} 。key为field，value为变量值或变量名的映射

  4. 构造feature2field字典，本质就是把步骤3中的field字典的k-v交换位置

  5. 最终模型的输入数据为（None，n+1），其中n个离散变量的特征，取值为0/1，1个连续变量的特征，取值为连续值（需要归一化）

7.1.2 输出部分

  1. 输出y 由0/1分类转换为-1/1分类

  2. 构造字典{1：n+2，-1：n+3}作为输出

  3. 构造训练集需要的字典field_dict，包括输入数据和输出数据，例如：{‘c1’:{1008:0,1001:1}，'c2':{0:6,1:7}}

7.2 注意事项

  1. 原始FFM论文中的结论：隐向量的维度 k值的调整提升效果不明显。

  2. 为了使用FFM方法，所有的特征必须转换成“field_id:feat_id:value”格式，field_id代表特征所属field的编号，feat_id是特征编号，value是特征的值。

  3. numerical数值型的特征比较容易处理，只需分配单独的field编号，如用户评论得分、商品的历史CTR/CVR等。优点是快速简单，不需要预处理，但是缺点也很明显，离群点影响，值的波动大等。因此可对numerical数值型特征采用连续值离散化或分箱下的连续值离散化的方法，将其转化为categorical类别型特征。

  4. categorical类别型特征需要经过One-Hot编码成数值型，编码产生的所有特征同属于一个field，而特征的值只能是0或1，如用户的性别、年龄段，商品的品类id等。

  5. 样本归一化。FFM默认是进行样本数据的归一化，若不进行数据样本的归一化，很容易造成数据inf溢出，进而引起梯度计算的nan错误。因此，样本层面的数据是推荐进行归一化的。

  6. 特征归一化。CTR/CVR模型采用了多种类型的源特征，包括数值型和categorical类型等。但是，categorical类编码后的特征取值只有0或1，较大的数值型特征会造成样本归一化后categorical类生成特征的值非常小，没有区分性。例如，一条用户-商品记录，用户为“男”性，商品的销量是5000个（假设其它特征的值为零），那么归一化后特征“sex=male”（性别为男）的值略小于0.0002，而“volume”（销量）的值近似为1。特征“sex=male”在这个样本中的作用几乎可以忽略不计，这是相当不合理的。因此，将源数值型特征的值归一化也是非常必要的。

  7. 省略零值特征。从FFM模型的表达式可以看出，零值特征对模型完全没有贡献。包含零值特征的一次项和组合项均为零，对于训练模型参数或者目标值预估是没有作用的。因此，可以省去零值特征，提高FFM模型训练和预测的速度，这也是稀疏样本采用FFM的显著优势。

8. 参考文献

[1] 深入FFM原理与实践

[2] FM系列算法解读（FM+FFM+DeepFM）

[3] 推荐算法之FFM：原理及实现简介

 

posted @ 2018-10-21 00:28  Bo_hemian  阅读(12362)  评论(5)  编辑  收藏  举报