词嵌入技术解析(一)
1. 词向量介绍
在讨论词嵌入之前,先要理解词向量的表达形式,注意,这里的词向量不是指Word2Vec。关于词向量的表达,现阶段采用的主要有One hot representation和Distributed representation两种表现形式。
1.1 One hot representation
顾名思义,采用独热编码的方式对每个词进行表示。
例如,一段描述“杭州和上海今天有雨”,通过分词工具可以把这段描述分为[‘杭州’,‘和’,‘上海’,今天’,‘有’,‘雨’],因此词表的长度为6,那么‘杭州’、‘上海’、'今天'的One hot representation分别为[1 0 0 0 0 0],[0 0 1 0 0 0],[0 0 0 1 0 0]。
可以看到,One hot representation编码的每个词都是一个维度,元素非0即1,且词与词之间彼此相互独立。
1.2 Distributed representation
Distributed representation在One hot representation的基础上考虑到词与词之间的联系,例如词义、词性等信息。每一个维度元素不再是0或1,而是连续的实数,表示不同的程度。Distributed representation 又包含了以下三种处理方式:
- 基于矩阵的分布表示。,矩阵中的一行,就成为了对应词的表示,这种表示描述了该词的上下文的分布。由于分布假说认为上下文相似的词,其语义也相似,因此在这种表示下,两个词的语义相似度可以直接转化为两个向量的空间距离。
- 基于聚类的分布表示。
- 基于神经网络的分布表示。
而我们现在常说的Distributed representation主要是基于神经网络的分布式表示的。例如‘杭州’、‘上海’的Distributed representation分别为[0.3 1.2 0.8 0.7] 和 [0.5 1.2 0.6 0.8 ] 。
所以对于词嵌入,我们可以理解为是对词的一种分布式表达方式,并且是从高维稀疏向量映射到了相对低维的实数向量上。
2. 为什么使用词嵌入
词嵌入,往往和Distributed representation联系在一起。这里主要从计算效率、词关系和数量这三点说明。
- 计算效率。采用One hot representation的每个词的向量长度是由词汇表的数量决定,如果词汇表数量很大,那么每个词的长度会很长,同时,由于向量元素只有一个元素为1,其余元素为0,所以,每个词的向量表达也会非常稀疏。而对于海量的词语来讲,计算效率是需要考虑的。
- 词关系。和One hot representation相比,Distributed representation能够表达词与词之间的关系。
- 数量。对于把词语作为模型输入的任务,对于相似的词语,可以通过较少样本完成目标任务的训练,而这是One hot representation所无法企及的优势。
3. Language Models
由于词嵌入目的是为了能更好地对NLP的输入做预处理。所以在对词嵌入技术作进一步讨论之前,有必要对语言模型的发展做一些介绍。
3.1 Bag of words model
Bag of words model又称为词袋模型,顾名思义,一段文本可以用一个装着这些词的袋子来表示。词袋模型通常将单词和句子表示为数字向量的形式,其中向量元素为句子中此单词在词袋表出现的次数。然后将数字向量输入分类器(例如Naive Bayes),进而对输出进行预测。这种表示方式不考虑文法以及词的顺序。
例如以下两个句子:
- John likes to watch movies. Mary likes movies too.
- John also likes to watch football games.
基于以上两个句子,可以建构词袋表:[ "John", "likes", "to", "watch", "movies", "also", "football", "games", "Mary", "too" ]
由于词袋表的长度为10,所以每个句子的数字向量表示长度也为10。下面是每个句子的向量表示形式:
- [1, 2, 1, 1, 2, 0, 0, 0, 1, 1]
- [1, 1, 1, 1, 0, 1, 1, 1, 0, 0]
Bag of words model的优缺点很明显:优点是基于频率统计方法,易于理解。缺点是它的假设(单词之间完全独立)过于强大,无法建立准确的模型。
3.2 N-Gram model
N-gram model的提出旨在减少传统Bag of words model的一些强假设。
语言模型试图预测在给定前t个单词的前提下观察t第 + 1个单词w t + 1的概率:
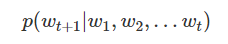
利用概率的链式法则,我们可以计算出观察整个句子的概率:
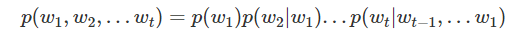
可以发现,估计这些概率可能是困难的。因此可以用最大似然估计对每个概率进行计算:

然而,即使使用最大似然估计方法进行计算,仍然非常困难:我们通常无法从语料库中观察到足够多的数据,并且计算长度仍然很长。因此采用了马尔可夫链的思想。
马尔可夫链规定:系统下一时刻的状态仅由当前状态决定,不依赖于以往的任何状态。即第t + 1个单词的发生概率表示为:
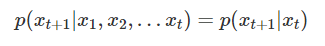
因此,一个句子的概率可以表示为:
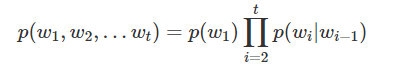
同样地,马尔可夫假设可以推广到:系统下一时刻的状态仅由当前0个、1个、2个...n个状态决定。这就是N-gram model的N的意思:对下一时刻的状态设置当前状态的个数。下面分别给出了unigram(一元模型)和bigram(二元模型)的第t + 1个单词的发生概率:
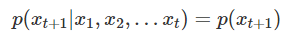

可以发现,N-Gram model 在Bag of words model的基础上,通过采用马尔科夫链的思想,减少了概率计算的复杂度,同时考虑了单词间的相关性。
3.3 Word2Vec Model
Word2Vec模型实际上分为了两个部分,第一部分为训练数据集的构造,第二部分是通过模型获取词嵌入向量,即word embedding。
Word2Vec的整个建模过程实际上与自编码器(auto-encoder)的思想很相似,即先基于训练数据构建一个神经网络,当这个模型训练好以后,并不会用这个训练好的模型处理新任务,而真正需要的是这个模型通过训练数据所更新到的参数。
关于word embedding的发展,由于考虑上下文关系,所以模型的输入和输出分别是词汇表中的词组成,进而产生出了两种词模型方法:Skip-Gram和CBOW。同时,在隐藏层-输出层,也从softmax()方法演化到了分层softmax和negative sample方法。
所以,要拿到每个词的词嵌入向量,首先需要理解Skip-Gram和CBOW。下图展示了CBOW和Skip-Gram的网络结构:
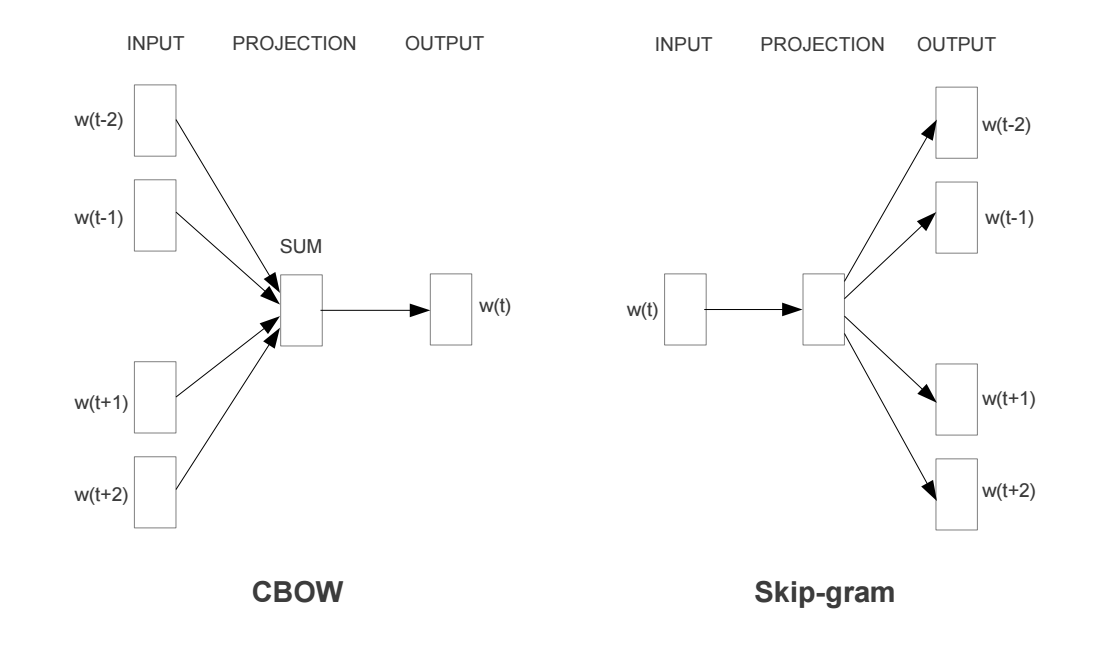
本文以Skip-Gram为例,来理解词嵌入的相关知识。Skip-Gram是给定input word来预测上下文。我们可以用小学英语课上的造句来帮助理解,例如:“The __________”。
关于Skip-Gram的模型结构,主要分为几下几步:
- 从句子中定义一个中心词,即Skip-Gram的模型input word
- 定义skip_window参数,用于表示从当前input word的一侧(左边及右边)选取词的数量。
- 根据中心词和skip_window,构建窗口列表。
- 定义num_skips参数,用于表示从当前窗口列表中选择多少个不同的词作为output word。
假设有一句子"The quick brown fox jumps over the lazy dog" ,设定的窗口大小为2(),也就是说仅选中心词(input word)前后各两个词和中心词(input word)进行组合。如下图所示,以步长为1对中心词进行滑动,其中蓝色代表input word,方框代表位于窗口列表的词。

所以,我们可以使用Skip-Gram构建出神经网络的训练数据。
我们需要明白,不能把一个词作为文本字符串输入到神经网络中,所以我们需要一种方法把词进行编码进而输入到网络。为了做到这一点,首先从需要训练的文档中构建出一个词汇表,假设有10,000个各不相同的词组成的词汇表。那么需要做的就是把每一个词做One hot representation。此外神经网络的输出是一个单一的向量(也有10000个分量),它包含了词汇表中每一个词随机选择附近的一个词的概率。
3.4 Skip-Gram网络结构
下图是需要训练的神经网络结构。左侧的神经元Input Vector是词汇表中进行One hot representation后的一个词,右侧的每一个神经元则代表着词汇表的每一个词。实际上,在对该神经网络feed训练数据进行训练时,不仅输入词input word(中心词)是用One hot representation表示,输出词output word也是用One hot representation进行表示。但当对此网络进行评估预测时,输出向量实际上是通过softmax()函数计算得到的一个词汇表所有词的概率分布(即一堆浮点值,而不是一个One hot representation)。
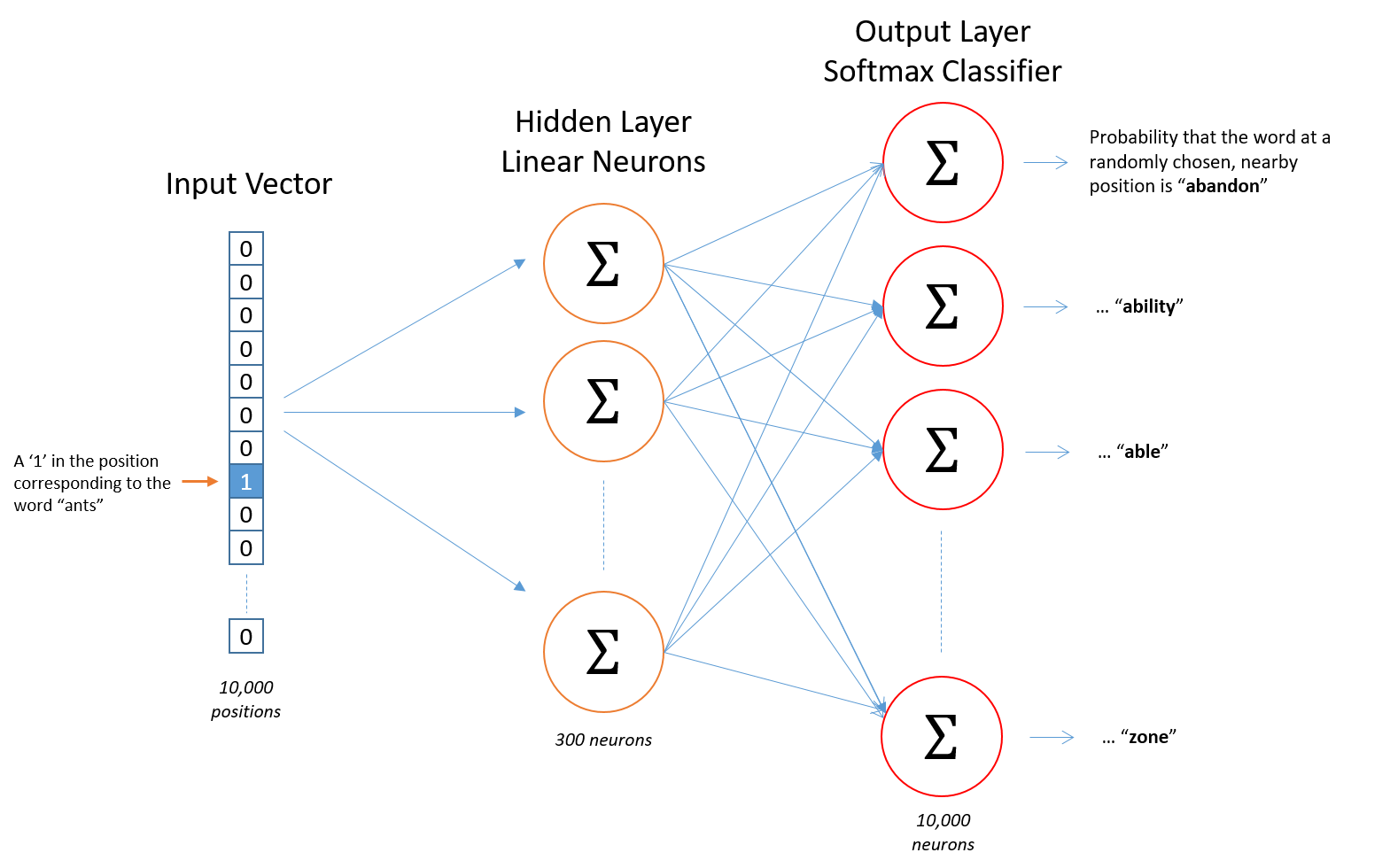
3.5 Word2Vec Model隐藏层
假设我们正在学习具有300个特征的词向量。因此,隐藏层将由一个包含10,000行(每个单词对应一行)和300列(每个隐藏神经元对应一列)的权重矩阵来表示。(注:谷歌在其发布的模型中的隐藏层使用了300个输出(特征),这些特征是在谷歌新闻数据集中训练出来的(您可以从这里下载)。特征的数量300则是模型进行调优选择后的“超参数”)。
下面左右两张图分别从不同角度代表了输入层-隐层的权重矩阵。

从左图看,每一列代表一个One hot representation的词和隐层单个神经元连接的权重向量。从右图看,每一行实际上代表了每个词的词向量,或者词嵌入。
所以我们的目标就是学习输入层-隐藏层的权矩阵,而隐藏层-输出层的部分,则是在模型训练完毕后不需要保存的参数。这一点,与自编码器的设计思想是类似的。
你可能会问自己,难道真的分别要把每一个One hot representation的词(1 x 10000)与一个10000 x 300的权矩阵相乘吗?实际上,并不是这样。由于One hot representation的词具有只有一个元素这为1,其余元素值为0的特性,所以可以通过查找One hot representation中元素为1的位置索引,进而获得对应要乘以的10000 x 300的权矩阵的向量值,从而解决计算速度缓慢的问题。下图的例子,可帮助我们进一步理解。

可以看到,One hot representation中元素为1的位置索引为3,所以只需要乘以10000 x 300的权矩阵中位置索引同样为3的向量值即可得到相应的输出。
3.6 Word2Vec Model输出层
下面是计算“car”这个单词的输出神经元的输出的例子:

4. 基于Tensorflow的Skip-Gram极简实现
网上找了一些Tensorflow版本的skip-gram实现,但都有一个问题,输入单词并没有按照论文的要求做One hot representation,不知道是不是出于计算速度方面的考虑。因此,本小节的代码还是遵循原论文的描述,对输入单词及输出单词首先做了One hot representation。
首先,是训练数据的构造,包括skip_window上下文参数、词的One hot representation以及中心词、输出词对的构造。
import numpy as np corpus_raw = 'He is the king . The king is royal . She is the royal queen ' # 大小写转换 corpus_raw = corpus_raw.lower() words = [] for word in corpus_raw.split(): if word != '.': words.append(word) # 创建一个字典,将单词转换为整数,并将整数转换为单词。 words = set(words) word2int = {} int2word = {} vocab_size = len(words) for i, word in enumerate(words): word2int[word] = i int2word[i] = word raw_sentences = corpus_raw.split('.') sentences = [] for sentence in raw_sentences: sentences.append(sentence.split()) # 构造训练数据 WINDOW_SIZE = 2 data = [] for sentence in sentences: for word_index, word in enumerate(sentence): for nb_word in sentence[max(word_index - WINDOW_SIZE, 0): min(word_index + WINDOW_SIZE, len(sentence)) + 1]: if nb_word != word: data.append([word, nb_word]) # one-hot编码 def to_one_hot(data_point_index, vocab_size): """ 对单词进行one-hot representation :param data_point_index: 单词在词汇表的位置索引 :param vocab_size: 词汇表大小 :return: 1 x vocab_size 的one-hot representatio """ temp = np.zeros(vocab_size) temp[data_point_index] = 1 return temp # 输入单词和输出单词 x_train = [] y_train = [] for data_word in data: x_train.append(to_one_hot(word2int[data_word[0]], vocab_size)) y_train.append(to_one_hot(word2int[data_word[1]], vocab_size))
其次,是Tensorflow计算图的构造,包括输入输出的定义、输入层-隐藏层,隐藏层-输出层的构造以及损失函数、优化器的构造。最后输出每个词的word embedding。具体代码如下所示:
import tensorflow as tf # 定义输入、输出占位符 x = tf.placeholder(tf.float32, shape=(None, vocab_size)) y_label = tf.placeholder(tf.float32, shape=(None, vocab_size)) # 定义word embedding向量长度 EMBEDDING_DIM = 5 # 隐藏层构造 W1 = tf.Variable(tf.random_normal([vocab_size, EMBEDDING_DIM])) b1 = tf.Variable(tf.random_normal([EMBEDDING_DIM])) # bias hidden_representation = tf.add(tf.matmul(x, W1), b1) # 输出层构造 W2 = tf.Variable(tf.random_normal([EMBEDDING_DIM, vocab_size])) b2 = tf.Variable(tf.random_normal([vocab_size])) prediction = tf.nn.softmax(tf.add(tf.matmul(hidden_representation, W2), b2)) # 构建会话并初始化所有参数 sess = tf.Session() init = tf.global_variables_initializer() sess.run(init) # 定义损失,这里只是采用常规DNN+softmax,未使用分层softmax和negative sample cross_entropy_loss = tf.reduce_mean(-tf.reduce_sum(y_label * tf.log(prediction), reduction_indices=[1])) # 优化器 train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cross_entropy_loss) n_iters = 10000 # train for n_iter iterations for _ in range(n_iters): sess.run(train_step, feed_dict={x: x_train, y_label: y_train}) # print('loss is : ', sess.run(cross_entropy_loss, feed_dict={x: x_train, y_label: y_train})) # 词嵌入 word embedding vectors = sess.run(W1 + b1) print('word embedding:') print(vectors)
上述代码的计算图可以简单表示为以下形式:
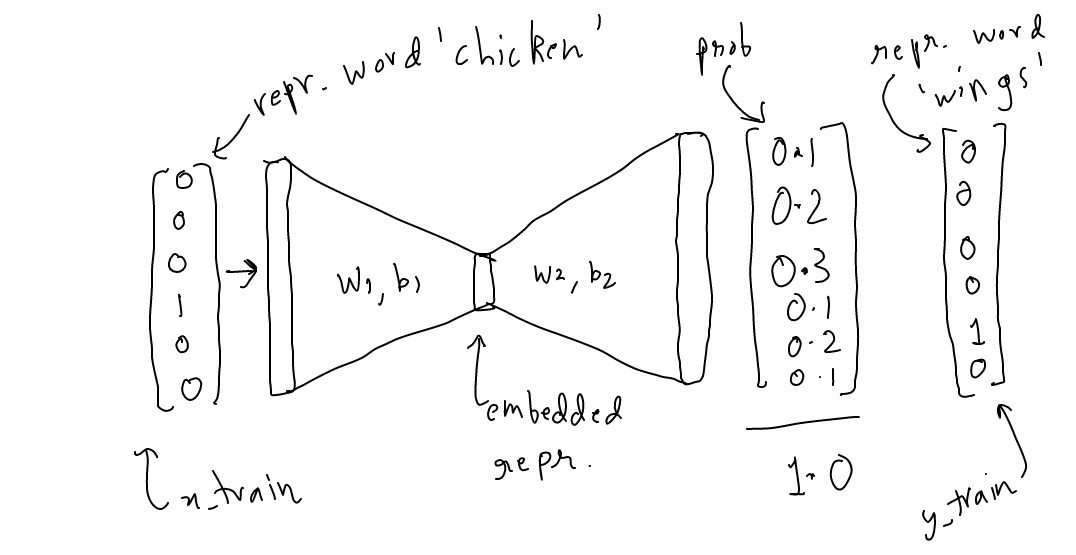
最后,打印出每个单词的词嵌入向量如下所示:
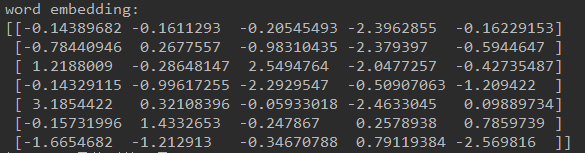
当词嵌入向量训练完成后,我们可以进行一个简单的测试,这里通过计算词嵌入向量间的欧氏距离寻找相近的词:
# 测试 def euclidean_dist(vec1, vec2): """欧氏距离""" return np.sqrt(np.sum((vec1 - vec2) ** 2)) def find_closest(word_index, vectors): min_dist = 10000 # to act like positive infinity min_index = -1 query_vector = vectors[word_index] for index, vector in enumerate(vectors): if euclidean_dist(vector, query_vector) < min_dist and not np.array_equal(vector, query_vector): min_dist = euclidean_dist(vector, query_vector) min_index = index return min_index print('与 king 最接近的词是:', int2word[find_closest(word2int['king'], vectors)]) print('与 queen 最接近的词是:', int2word[find_closest(word2int['queen'], vectors)]) print('与 royal 最接近的词是:', int2word[find_closest(word2int['royal'], vectors)])
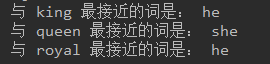
下面是输出的测试结果:
5. 总结
- 词嵌入是一种把词从高维稀疏向量映射到了相对低维的实数向量上的表达方式。
- Skip-Gram和CBOW的作用是构造神经网络的训练数据。
- 目前设计的网络结构实际上是由DNN+softmax()组成。
- 由于每个输入向量有且仅有一个元素为1,其余元素为0,所以计算词嵌入向量实际上就是在计算隐藏层的权矩阵。
- 对于单位矩阵的每一维(行)与实矩阵相乘,可以简化为查找元素1的位置索引从而快速完成计算。
6. 结束了吗?
仔细阅读代码,我们发现prediction时,使用的是softmax()。即输入词在输出层分别对词汇表的每一个词进行概率计算,如果在海量词汇表的前提下,计算效率是否需要考虑在内?有没有更快的计算方式呢?
此外,本文第3节提到的分层softmax是什么?negative samples又是什么?Huffman code又是怎样使用的?关于这些问题的思考,请关注:词嵌入的那些事儿(二)
7. 参考资料
[1] Word2Vec Tutorial - The Skip-Gram Model


 浙公网安备 33010602011771号
浙公网安备 33010602011771号