js数据结构之二叉树

二叉树实现如下

    function Node(data, left, right){
        // 保存当前节点key值
        this.data = data
        // 指向左子节点
        this.left = left
        // 指向右子节点
        this.right = right
    }
    function BST() {
        this.root = null
        this.show = () => {
            return this.root;
        };
        // 插入节点
        this.insert = function(data){
            let node = new Node(data,null,null)
            if(this.root == null){ // 这时没有根节点
                this.root = node
            } else {
                let current = this.root
                let parent;
                while(true){
                    parent = current
                    //当插入的值小于根节点的值时，将值作为左节点插入
                    if(data < current.data){
                        current = current.left;
                        if (current === null) {
                            parent.left = node;
                            break;
                        }
                    } else {
                        current = current.right;
                        if(current === null) {
                            parent.right = node;
                            break;
                        }
                    }
                }
            }
        }
       // 先序遍历
        this.preOrder = function(node){
            let result = []
            let pre = function(node) {
                if (node) {
                    result.push(node.data)
                    pre(node.left)
                    pre(node.right)
                }
                
            }
            pre(node)
            return result
        }
       // 中序遍历
       this.inOrder = function(node){
            let result = []
            let inTraverse = function(node) {
                if (node) {
                    inTraverse(node.left)
                    result.push(node.data)
                    inTraverse(node.right)
                }
                
            }
            inTraverse(node)
            return result
        }
         // 后序遍历
       this.afterOrder  = function(node){
            let result = []
            let afterTraverse = function(node) {
                if (node) {
                    afterTraverse(node.left)
                    afterTraverse(node.right)
                    result.push(node.data)
                }
                
            }
            afterTraverse(node)
            return result
        }
       // 获得最小值的节点
       this.getMin = function() {
            let current = this.root
            while(current.left) {
                current = current.left
            }
            return current.data
       }
       // 获得最大值的节点
       this.getMax = function() {
            let current = this.root
            while(current.right) {
                current = current.right
            }
            return current.data
       }
        // 寻找给定数据的节点
        this.find = function(data){
            let current = this.root
            while(current){
                if(current.data == data) {
                    return current
                } else if(data < current.data) {
                    current = current.left
                } else {
                    current = current.right
                }
            }
            return null;
        }
        // 删除节点
        this.remove = function(data) {
            this.root = this._removeNode(this.root,data)
        }
        // 删除节点时，一共可以分为三种情况
        // 1.待删除的节点是叶子节点。
        // 2.待删除的节点没有左子节点，或者没有右子节点。
        // 3.待删除的节点的左右子节点均存在。
        this._getSmallest = function(node){
            while(node.left){
                node = node.left
            }
            return node
        }
        this._removeNode = function(node,data) {
            if(node == null) {
                return null
            }
            if(data == node.data){
                // 叶子节点
                if(node.left == null && node.right ==null) {
                    return null
                }
                // 没有左节点的节点
                if (node.left == null) {
                    return node.right
                }
                // 没有右节点的节点
                if (node.right == null) {
                    return node.left
                }
                 // 有两个节点的节点
                /*
                    做法：
                        找到待删节点的右子树上的最小值创建一个临时节点
                        将临时节点上的值复制到待删节点，然后再删除临时节点
                */
                // 寻找右节点的最小值
                let tmpNode = this._getSmallest(node.right)
                node.data = tmpNode.data
                node.right = this._removeNode(node.right,tmpNode.data)
                return node
            } else if(data < node.data) { // 待删节点在左子树上
                node.left = this._removeNode(node.left,data)
                return node
            } else {   // 待删除节点在右子树上
                node.right = this._removeNode(node.right, data);
                return node;
            }
        }
    }

 

测试

插入节点 及 遍历

let bst = new BST()
bst.insert(20)
bst.insert(8)
bst.insert(7)
bst.insert(22)
bst.insert(15)
bst.insert(21)
bst.insert(32)
bst.insert(11)
bst.insert(16)
bst.insert(48)

  console.log(bst.preOrder(bst.root)) // 先序遍历： [20, 11, 7, 15, 16, 22, 21, 32, 48]

  console.log(bst.inOrder(bst.root)) // 中序遍历： [7, 11, 15, 16, 20, 21, 22, 32, 48]

  console.log(bst.afterOrder(bst.root)) // 后序遍历： [7, 16, 15, 11, 21, 48, 32, 22, 20]

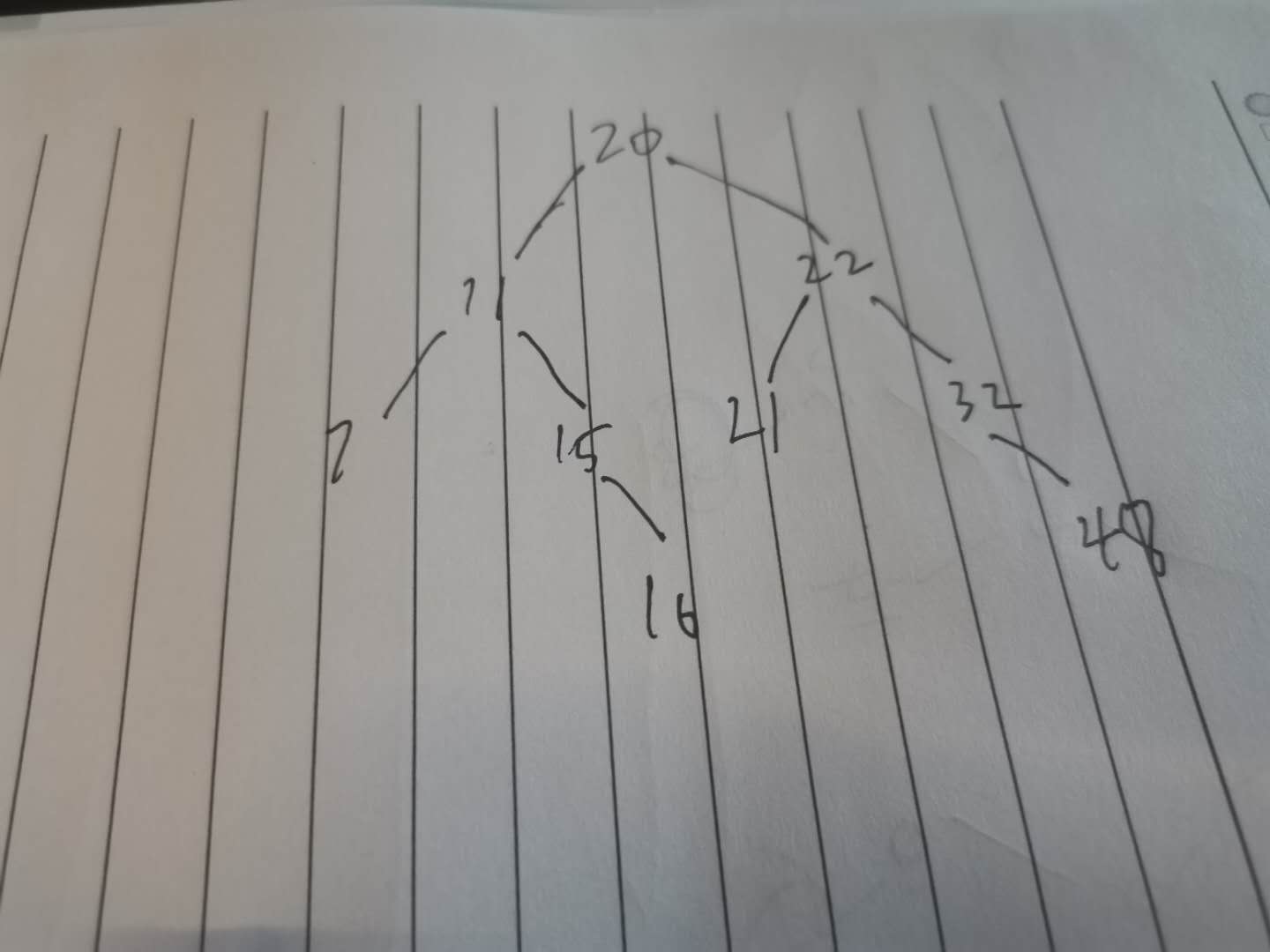
新建后的二叉排序树如下图所示

 

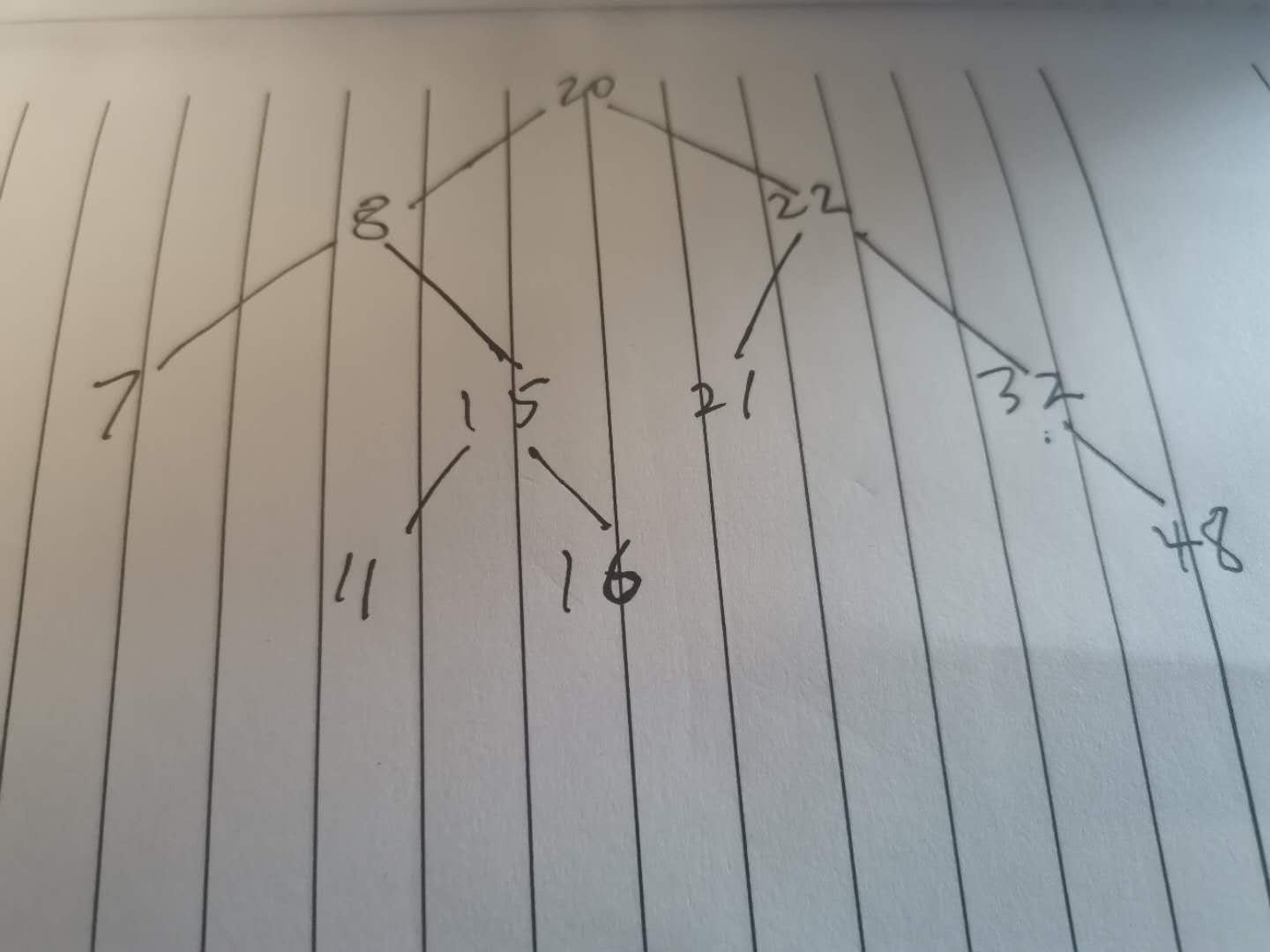
删除节点8

bst.remove(8)

 

删除后的二叉排序树如下图所示