CF102920L Two Buildings【分治】【决策单调性】
优秀的分治题目。是“2020-2021 ACM-ICPC, Asia Seoul Regional Contest”的一道题。
Description
There are \(n\) buildings along a horizontal street. The buildings are next to each other along the street, and the \(i\)-th building from left to right has width \(1\) and height \(h_i\). Among the \(n\) buildings, we are to find two buildings, say the \(i\)-th building and \(j\)-th building with \(i<j\), such that \((h_i+h_j)*(j−i)\) is maximized.
For example, the right figure shows \(5\) buildings, with heights \(1\), \(3\), \(2\), \(5\), \(4\), from left to right. If we choose the first \(2\) buildings, then we get \((1+3)*(2−1)=4\). If we choose the first and fifth buildings, then we \((1+4)*(5−1)=20\). The maximum value is achieved by the second and fifth buildings with heights \(3\) and \(4\), respectively: \((3+4)*(5−2)=21\).
Write a program that, given a sequence of building heights, prints \(\max_{1\le i<j\le n}(h_i+h_j)*(j−i)\).
Input
Your program is to read from standard input. The input starts with a line containing an integer \(n\) (\(2\le n\le 1,000,000\)), where \(n\) is the number of buildings. The buildings are numbered \(1\) to \(n\) from left to right. The second line contains the heights of \(n\) buildings separated by a space such that the \(i\)-th number is the height \(h_i\) of the \(i\)-th building (\(1\le h_i\le 1,000,000\)).
Output
Your program is to write to standard output. Print exactly one line. The line should contain \(\max_{1\le i<j\le n}(h_i+h_j)*(j−i)\).
Examples
input
5 1 3 2 5 4output
21input
5 8 3 6 3 1output
36
题意:
有 \(n(2\le n\le 1000000)\) 栋楼房,第 \(i\) 栋高度为 \(h_i(1\le h_1\le 1000000)\)。问两栋楼房所能构成的 \((h_i+h_j)*(j−i)\) 最大值是多少。
题解:
为了方便,我们把要求的式子转化为 \((h_i-(-h_j))\times(j-i)\),这样构造出数列 \(-h_i\),就是坐标系中 \(x\) 轴上方和 \(x\) 轴下方两个数列中选出两个 \(h\) 进行计算。
如果存在 \(i<j\),同时 \(-h_i<-h_j\),那么 \(j\) 一定比 \(i\) 更优。可以用单调栈来把数列 \(\{h_i\}\) 和 \(\{-h_i\}\) 都变为单调的。得到单增的 \(\{H_i\}\) 和 \(\{-H_i\}\)。
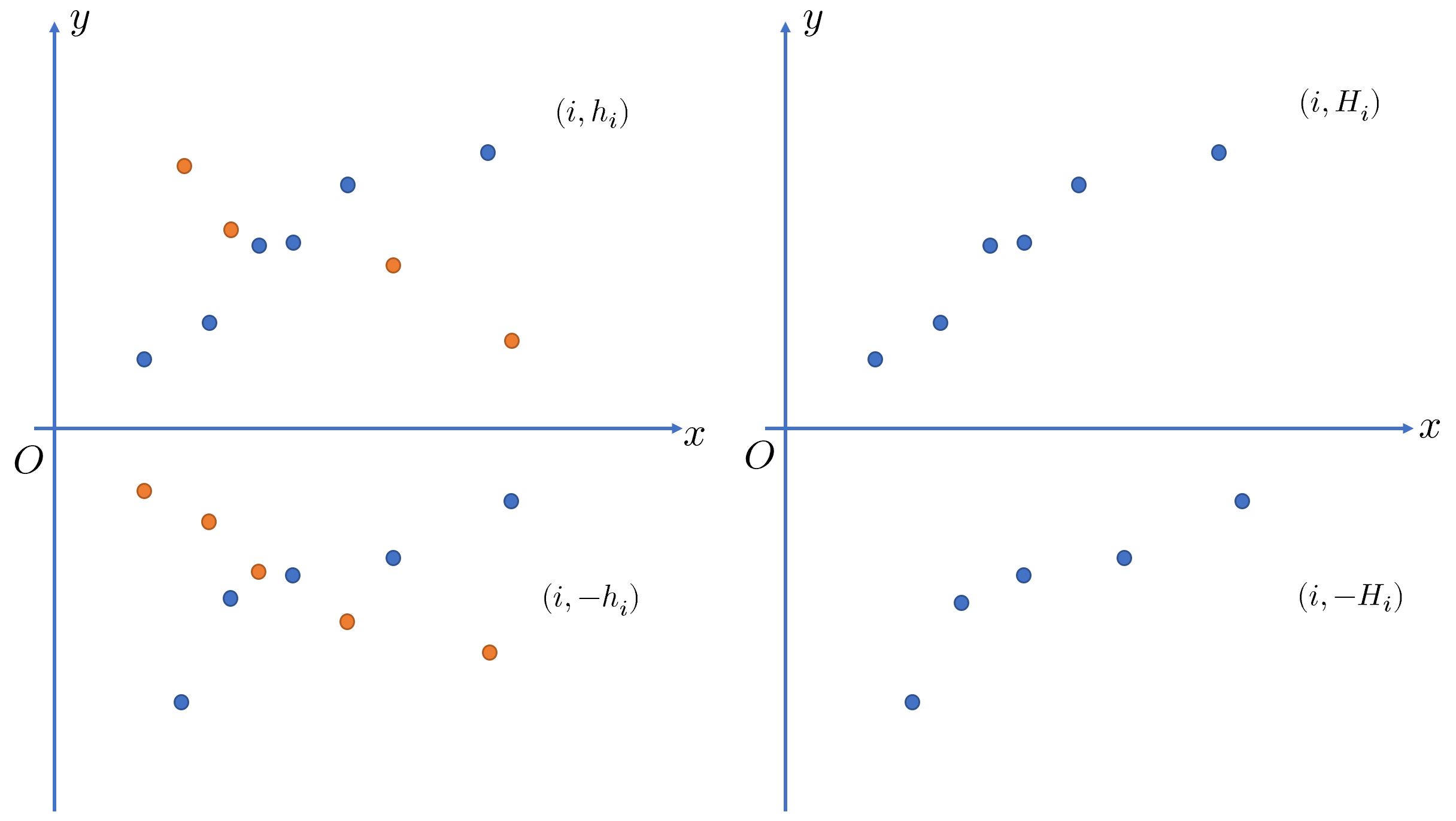
如图,图中橙色的点删除后,对答案产生贡献的点只会在蓝色中产生。
而蓝色的点 \(\{H_i\}\) 和 \(\{-H_i\}\) 对应了两段递增的序列(此时下标 \(i\) 不一定连续)。最终答案为 \([H_i-(-H_j)]\times(j-i)\)。假设对于选定的 \(H_i\),对应 \(-H_j\) 为最优解,即 \(\forall k>j,[H_i-(-H_j)]\times(j-i)\geqslant[H_i-(-H_k)]\times(k-i)\),可知
因此对于 \(l<i\),对上式进行放缩,得
所以当 \(H_i\) 对应的最优解位置为 \(-H_j\) 时,\(l<i\) 的 \(H_l\) 对应的最优解位置 \(-H_k\) 满足 \(k\geqslant j\)。
如果上式推导过于复杂,它对应的图形推导如下。

左图中,如果 \(H_i\) 对应的最优解是 \(H_j\),那么①的面积 \(S_1\) 一定比②的 \(S_2\) 大。右图中,那么对 \(l<i\),已知 \(S_1\geqslant S_2\),有 \(S_1+S_3\geqslant S_2-S_4\),所以 \(l\) 对应的最优解一定不会在 \(j\) 右边。
此时再考虑上边的推导,便能清楚理解了。
分治递归,时间复杂度为 \(O(n\log n)\)。
Code:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
#define ll long long
int a[1001000],b[1001000],c[1001000];
int bp[1001000],cp[1001000];
ll ans=0;
void solve(int l,int r,int L,int R)
{
if(l>r)
return;
int mid=(l+r)>>1,q=0;
ll Ans=0;
for(int i=L;i<=R;++i)
{
if(Ans<1ll*(cp[i]-bp[mid])*(b[mid]+c[i]))
{
q=i;
Ans=1ll*(cp[i]-bp[mid])*(b[mid]+c[i]);
}
}
ans=ans>Ans?ans:Ans;
solve(l,mid-1,L,q);
solve(mid+1,r,q,R);
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i)
scanf("%d",&a[i]);
int ii=0,iii=0;
c[0]=1e8;
for(int i=1;i<=n;++i)
{
if(a[i]>b[ii])
{
b[++ii]=a[i];
bp[ii]=i;
}
while(a[i]>=c[iii])
--iii;
c[++iii]=a[i];
cp[iii]=i;
}
solve(1,ii,1,iii);
printf("%lld\n",ans);
return 0;
}

