第八章学习小结
本章学习的是排序
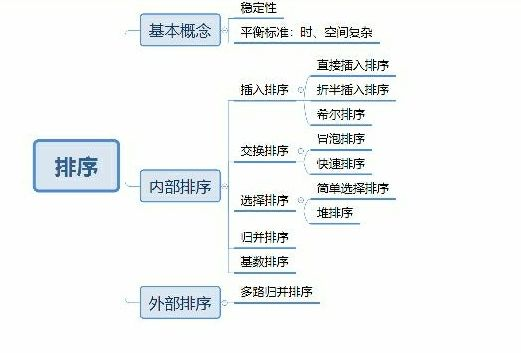
一、
插入排序:是一个稳定的排序方法(时间复杂度:O(n²))
(1)直接插入排序: 从待排序的第二个元素开始,向下扫描列表,比较这个目标值target与arr[i-1]、arr[i-2]的大小,依次类推。如果target的值小于于或等于每一个元素值,那么每个元素都会向右滑动一个位置,一旦确定了正确位置j,目标值target(即原始的arr[i])就会被复制到这个位置。
void InsertSort (ElemType A[], int n)
{
int i,j;
for(i=2;i<=n;i++)
if(A[i].key<A[i-1].key)
{
A[0]=A[i];
for(j=i-1;A[0].key<A[j].key;--j)
A[j+i]=A[j];
A[j+i]=A[0];
}
}
(2)折半插入排序:
与二分法类似,不断对折平分,改变上界和下界,直到找到数据合适的位置,再将数据插入
时间复杂度为O(n^2),空间复杂度为O(1)
(3)希尔排序法:(不太懂)希尔排序是一种不稳定的排序方法(时间复杂度:O(N*logN))

(from:https://blog.csdn.net/Void_leng/article/details/87812430)
选择排序:
(1)简单选择排序:是一种不稳定的排序方法(时间复杂度: O(n²))
将待排序数组分为有序和无序两组(初始情况下有序组为空),从左向右扫描无序组,找出最小的元素,将其放置在无序组的第一个位置。至此有序组++,无序组--,重复操作,直至无序组只剩下一个元素。
//对表A作简单的选择排序,A[]从0开始放元素
for(i=0;i<=n-1;i++){ //一共进行n-1趟
min=i; //记录最小元素位置
for(j=i+1;j<n;j++) //在A[i...n-1]中选择最小的元素
if(A[j]<A[min])
min=j; //更新最小元素位置
if(min!=i) swap(A[i],A[min]); //在第n个元素交换
}
序列可以看做是完全二叉树,先调整堆(变为大根堆或者小根堆),然后不断将顶的记录(最大值)与未排序的最后一个记录(最小值)交换
大根堆:每个根结点都大于它的左右孩子结点
小根堆:每个根结点都小于它的左右孩子结点
交换排序:
(1)冒泡排序:是一种稳定排序算法(时间复杂度为O(n²))
两两比较相邻的记录值,如果反序则交换,直到没有反序的记录为准。对数组中的各数据,依次比较相邻的两元素的大小。如果前面的数据大于后面的数据,就交换这两个数据。经过第一轮的多次比较排序后,变可把最小的数据排好。再用同样的方法把剩下的数据逐个进行比较,最后便可按照从小到大的顺序排好数组各数据的顺序。
void BubbleSort (ElemType A[],int n){
//用冒泡排序将序列A中的元素按从小到大排列
for(i=0;i<n-1;i++){
flag=false; //标示本趟冒泡是否发生交换标志
for(j=n-1;j>i;j--) //一趟冒泡过程
if(A[j-i].key>A[j].key){ //若为逆序
swap(A[j-1],A[j]); //交换
flag=true;
}
if(flag==false)
return; //本趟遍历没有发生交换,说明已经有序
}
}
(2)快速排序:是一个不稳定的排序算法(时间复杂度为O(nlog2n))

from(https://blog.csdn.net/Void_leng/article/details/87812430)
归并排序:
将序列分为两份,然后再分别将左右两份又不断分成两份,直到分成每份只有两个数据,然后将数据排序,再两份两份的合并、排序
时间复杂度O(nlog2n),空间复杂度O(n)
二、
快要考试了,加油,努力复习。




