傅立叶变换系列(三)傅立叶变换
说明:
傅里叶级数、傅里叶变换、离散傅里叶变换、短时傅里叶变换。。。这些理解和应用都非常难,网上的文章有两个极端:“Esay” Or “Boring”!如果单独看一两篇文章就弄懂傅里叶,那说明你真的是大神了。
本博文是经过查阅网上几十篇大神的博客、文章、书籍等进行的一个汇总,希望对初学者和我自己一个入门和总结,所以本博文并非原创,抄袭+汇总+修改+总结!
主要参考:
1.傅里叶变换到小波变换的风趣讲解:https://zhuanlan.zhihu.com/p/22450818
2.一篇外文的翻译者,讲的非常好,本博文大部分基于此大神的翻译进行的部分优化:http://blog.csdn.net/dznlong
3.风趣幽默的讲解傅里叶的由来和一些基础:https://zhuanlan.zhihu.com/p/19763358
4.网上很多人都基于这篇外文进行的翻译和总结:http://www.dspguide.com/ch8/5.htm,外文得FQ,这里下载之后供大家下载:
5.扬州大学的一个PPT讲解傅里叶级数推导,原地址不知道在哪,这里给出好心人上传的百度地址:https://wenku.baidu.com/view/67a0cccdda38376baf1faec4.html
6.百度文库关于傅立叶级数到傅立叶变换的详细描述:https://wenku.baidu.com/view/365c63740b4c2e3f57276383.html
7.参考的博文在这里或者博文结尾给出,文中直接引用将不再进行说明,请见谅!
一.傅立叶变换的由来
看了前面的两个章节,我们是不是感觉傅立叶级数无敌了?为什么还要傅立叶变换啥玩意呢?
阅读前面的博文,我们已经清楚的知道如何使用傅立叶级数去描述任何一个周期函数,其中傅里叶级数将一个周期函数描述成离散频率正弦函数的组合,即在频域上离散。然而,我们要分析的函数中常常会有非周期函数,这就需要傅里叶变换而不是傅里叶级数来描述这类函数。频域不同于时域,是从另一个角度观察客观世界的一种方式。其将无限动态的世界看成是注定的和静止的。从频域理解世界,更像是上帝看世界的方式。
对于任何一个非周期函数,我们都可以认为其可以通过一个周期函数的周期趋于无穷转化而来。周期趋于无穷也就意味着频率趋于零,以及角速度ω趋于零。也就是说,一个非周期函数会通过傅里叶变换被描述成连续的正弦函数的组合,即在频域上连续。基于这个思想,傅里叶级数即将演化成傅里叶变换。
二.傅立叶变换的理论来历
由上面的分析可知,周期T变为无穷大的时候扔可使用傅立叶级数,当然这里有点不严谨,但是数学上无穷小和无穷大就是可以近似逼近,可以说是无差别吧!
那么我们就可以把傅立叶级数应用到非周期函数上面了,非周期函数可以看做周期T是无穷大啊!
以下是理论部分的推导和证明:


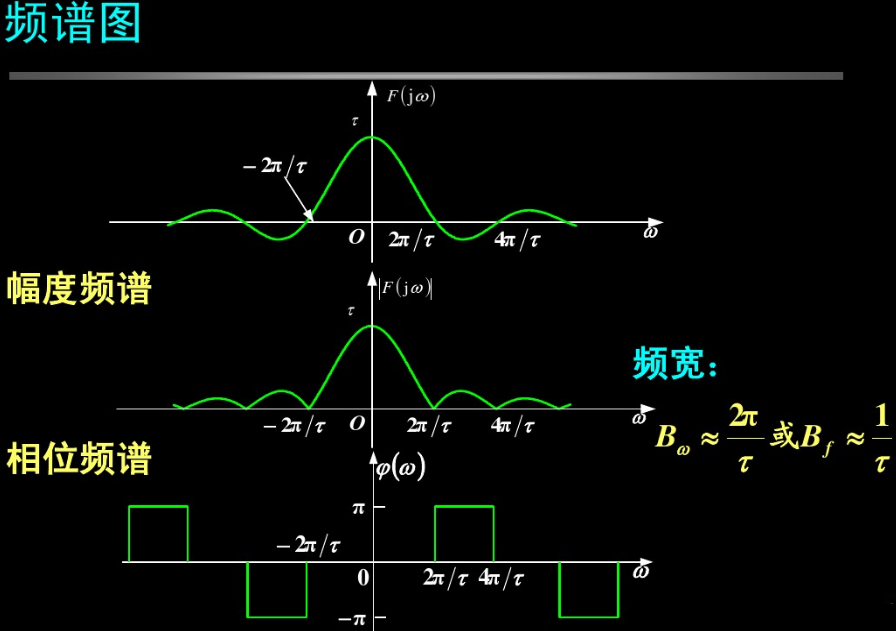
三.傅立叶变换的频谱图
下面给出了一个金典的例子,其实目的就是想告诉大家:
当T为无穷大的时候,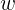 趋向与0,那么画图频谱图的时候就变得连续,和傅里叶级数全然不同!
趋向与0,那么画图频谱图的时候就变得连续,和傅里叶级数全然不同!
其实周期函数是非周期函数的一个特例,可以说傅立叶变换适用于周期和非周期函数,只要满足一些条件(这些条件集体查看上面给的链接)。

四.傅立叶变换的性质
傅立叶变换的性质很多,本博文是启发式和记录的目的,这里想深入的朋友请看:https://wenku.baidu.com/view/911f5d67ddccda38376baf41.html
记住几个常用的就可以了,证明没必要知道,在下直接复制没有进行证明!

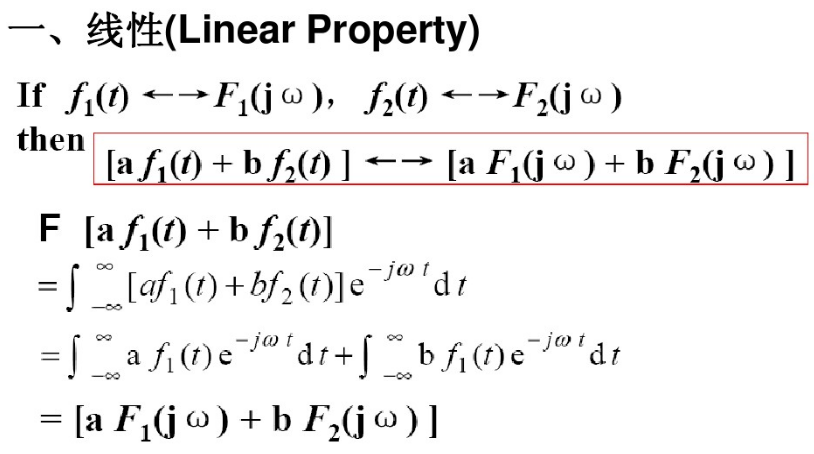









五.参考文章
类似我这种参考别人然后一个总结,说的不是很详细:http://blog.csdn.net/znculee/article/details/48291981
一篇外文,大概看了一点点挺好的:https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
文中的公式编辑器:http://www.codecogs.com/latex/eqneditor.php
部分参考博文开头已经给出,如果有参考没有给出地址的,请告知立马改正!
-------------------------------------------
个性签名:衣带渐宽终不悔,为伊消得人憔悴!
如果觉得这篇文章对你有小小的帮助的话,记得关注再下的公众号,同时在右下角点个“推荐”哦,博主在此感谢!


