傅立叶变换系列（一）傅立叶系列的由来

---

 说明：

　　傅里叶级数、傅里叶变换、离散傅里叶变换、短时傅里叶变换。。。这些理解和应用都非常难，网上的文章有两个极端：“Esay”  Or  “Boring”！如果单独看一两篇文章就弄懂傅里叶，那说明你真的是大神了。

　　本博文是经过查阅网上几十篇大神的博客、文章、书籍等进行的一个汇总，希望对初学者和我自己一个入门和总结，所以本博文并非原创，抄袭+汇总+修改+总结！

主要参考：

　　1.傅里叶变换到小波变换的风趣讲解：https://zhuanlan.zhihu.com/p/22450818

　　2.一篇外文的翻译者，讲的非常好，本博文大部分基于此大神的翻译进行的部分优化：http://blog.csdn.net/dznlong

　　3.风趣幽默的讲解傅里叶的由来和一些基础：https://zhuanlan.zhihu.com/p/19763358

　　4.网上很多人都基于这篇外文进行的翻译和总结：http://www.dspguide.com/ch8/5.htm，外文得FQ，这里下载之后供大家下载：

　　5.扬州大学的一个PPT讲解傅里叶级数推导，原地址不知道在哪，这里给出好心人上传的百度地址：https://wenku.baidu.com/view/67a0cccdda38376baf1faec4.html

　　6.百度文库关于傅立叶级数到傅立叶变换的详细描述：https://wenku.baidu.com/view/365c63740b4c2e3f57276383.html

　　7.参考的博文在这里或者博文结尾给出，文中直接引用将不再进行说明，请见谅！

---

 

一.傅立叶变换的前言

　　大家刚开始看傅里叶变换的时候，应该都会有几个问题：1.为什么会提出来这样的东西？2.这样的东西有什么用？怎么才能学好这个东西？

　　那么第一小节就按照这三个问题展开介绍：

　　1.1为什么会有傅立叶变换？

　　　　例一：举个数学的例子，如何求解：

.

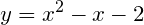　　　　基本每个人都会求解吧？

　　　　A.直接用公式求:

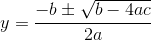
　　　　B.使用技巧:

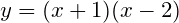
　　　　大家都知道使用B的方法“快准狠”，那么我们在求解问题的时候尽量选择更简单且效率高的方法去做。

　　　　例二：我们都知道“泰勒公式”，又长又难看，为什么使用这个公式呢？

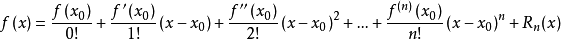
　　　　使用过的人都知道好处，没使用的人望闻生怯~~

　　　　假设给你一个，这个大家都会求解（直接作图看零点）--->>>

　　　　假设给你一个，这个你怎么作图？当然不能使用matlab或者其它工具了。

　　　　上面的式子用泰勒公式展开去求解就很简单了。。。

　　　　解决：现在给你一个傅里叶级数的展开：

　　　　看到一个f(x)化解成无数个sin(x)和cos(x)的求和，是不是知道这个f(x)很复杂，然后化解成正余弦函数去求解很方便。

　　　　你现在不用知道具体参数什么意思，知道这家伙怎么为什么来的就可以了。

　　1.2傅里叶变换有什么用？

　　　　现在有一个信号（如下图），假设最高的波是噪声，现在要去除这个噪声怎么去做？

　　　　当然你可以采集每一个点，然后比较大小的方法。这样的效率和精度我们还不如不去噪声！

 

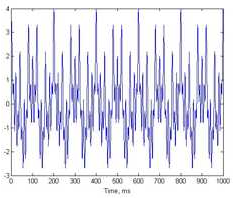
　　　　对这个信号进行傅里叶变换（具体怎么实现别管），我们发现这个信号是由四个频率的波合成的，那么既然最高的是噪声（100HZ），那么我们直接用低通滤波就可以了。

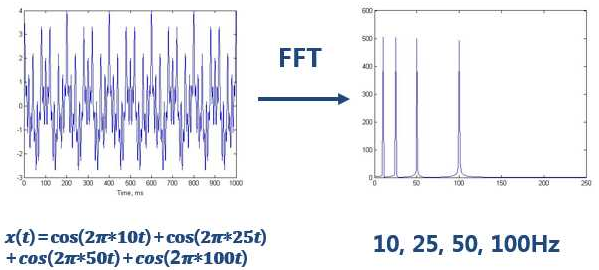
　　　　一些复杂的信号我们没办法直接找到规律，那么通过傅里叶变换之后会发现他们的规律，之后在进行处理就非常容易了。

　　1.3怎么才能学好傅里叶变换？

　　　　A.首先去看一些风趣幽默的讲解傅立叶的文章，对傅立叶有个映像，直接看书就是看天书（当然你有基础可以直接看书）

　　　　B.接着去看一些稍微专业的博文或者书籍，注意这里是“稍微”！对傅立叶的过程有个大概了解。

　　　　C.看看专业的书籍和PPT等，这里要知道哪些公式、哪些理论。

　　　　D.看推导的公式，看不懂就算了，有个了解。

　　　　F.实践，我是做图像的所以用别人写好的库拿图像实践，你可以拿信号~~

二.傅里叶变换的提出

　　傅立叶是一位法国数学家和物理学家的名字，英语原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier对热传递很感兴趣，于1807年在法国科学学会上发表了一篇论文，论文里描述运用正弦曲线来描述温度分布，论文里有个在当时具有争议性的决断：任何连续周期信号都可以由一组适当的正弦曲线组合而成。当时审查这个论文的人，其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827)，当拉普拉斯和其它审查者投票通过并要发表这个论文时，拉格朗日坚决反对，在近50年的时间里，拉格朗日坚持认为傅立叶的方法无法表示带有棱角的信号，如在方波中出现非连续变化斜率。法国科学学会屈服于拉格朗日的威望，否定了傅立叶的工作成果，幸运的是，傅立叶还有其它事情可忙，他参加了政治运动，随拿破仑远征埃及，法国大革命后因怕会被推上断头台而一直在逃避。直到拉格朗日死后15年这个论文才被发表出来。

       谁是对的呢？拉格朗日是对的：正弦曲线无法组合成一个带有棱角的信号。但是，我们可以用正弦曲线来非常逼近地表示它，逼近到两种表示方法不存在能量差别，基于此，傅立叶是对的。

       为什么我们要用正弦曲线来代替原来的曲线呢？如我们也还可以用方波或三角波来代替呀，分解信号的方法是无穷多的，但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单，因为正余弦拥有原信号所不具有的性质：正弦曲线保真度。一个正余弦曲线信号输入后，输出的仍是正余弦曲线，只有幅度和相位可能发生变化，但是频率和波的形状仍是一样的。且只有正余弦曲线才拥有这样的性质，正因如此我们才不用方波或三角波来表示。

　　2.1傅立叶变换的类型和表示方法

　　　　先看类型：

　　　　根据原信号的不同类型，我们可以把傅立叶变换分为四种类别：

　　　　当然其中还包括很多改进的划分，比如：快速傅立叶变换、短时傅立叶变换等。。。

　　　　我们主要的讲解针对：周期性连续信号、周期性非连续信号、非周期性连续信号 进行讲解，其它情况用的很少，我们不做讨论。

　　　　再看方法：　　　　

　　　　1、 序号表示方法，根据时域中信号的样本数取 0 ~ N/2，用这种方法在程序中使用起来可以更直接地取得每种频率的幅度值，因为频率值跟数组的序号是一一对应的:X[k]，取值范围是 0 ~ N/2；

　　　　2、 分数表示方法，根据时域中信号的样本数的比例值取 0 ~ 0.5: X[ƒ]，ƒ = k/N，取值范围是 0 ~ 1/2；　　　　

　　　　3、 用弧度值来表示，把ƒ乘以一个 2π得到一个弧度值，这种表示方法叫做自然频率(natural frequency)：X[ω]，ω = 2πƒ = 2πk/N，取值范围是 0 ~ π；　　　　

　　　　4、 以赫兹(Hz)为单位来表示，这个一般是应用于一些特殊应用，如取样率为 10 kHz表示每秒有 10,000 个样本数：取值范围是 0 到取样率的一半。 

　　　　是不是感觉有点懵逼？别着急，就当了解一下，下一篇将循序渐进的叙述这些方法。

 

三.参考文章

　　　　类似我这种参考别人然后一个总结，说的不是很详细：http://blog.csdn.net/znculee/article/details/48291981

　　　　一篇外文，大概看了一点点挺好的：https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/

　　　　文中的公式编辑器：http://www.codecogs.com/latex/eqneditor.php

　　　　部分参考博文开头已经给出，如果有参考没有给出地址的，请告知立马改正！