协方差和相关系数的概念和含义

 

1.协方差：

　　在概率论中，两个随机变量 X 与 Y 之间相互关系，大致有下列3种情况：

 

当 X, Y 的联合分布像上图那样时，我们可以看出，大致上有： X 越大  Y 也越大， X 越小  Y 也越小，这种情况，我们称为“正相关”。

 

当X, Y 的联合分布像上图那样时，我们可以看出，大致上有：X 越大Y 反而越小，X 越小 Y 反而越大，这种情况，我们称为“负相关”。

　　当X, Y  的联合分布像上图那样时，我们可以看出：既不是X  越大Y 也越大，也不是 X 越大 Y 反而越小，这种情况我们称为“不相关”。

怎样将这3种相关情况，用一个简单的数字表达出来呢？

在图中的区域（1）中，有 X>EX ，Y-EY>0 ，所以(X-EX)(Y-EY)>0；

在图中的区域（2）中，有 X<EX ，Y-EY>0 ，所以(X-EX)(Y-EY)<0；

在图中的区域（3）中，有 X<EX ，Y-EY<0 ，所以(X-EX)(Y-EY)>0；

在图中的区域（4）中，有 X>EX ，Y-EY<0 ，所以(X-EX)(Y-EY)<0。

　　当X 与Y 正相关时，它们的分布大部分在区域（1）和（3）中，小部分在区域（2）和（4）中，所以平均来说，有E(X-EX)(Y-EY)>0 。

　　当 X与 Y负相关时，它们的分布大部分在区域（2）和（4）中，小部分在区域（1）和（3）中，所以平均来说，有(X-EX)(Y-EY)<0 。

　　当 X与 Y不相关时，它们在区域（1）和（3）中的分布，与在区域（2）和（4）中的分布几乎一样多，所以平均来说，有(X-EX)(Y-EY)=0 。

所以，我们可以定义一个表示X, Y 相互关系的数字特征，也就是协方差：

cov(X, Y) = E(X-EX)(Y-EY)。

　　当 cov(X, Y)>0时，表明 X与Y 正相关；

　　当 cov(X, Y)<0时，表明X与Y负相关；

　　当 cov(X, Y)=0时，表明X与Y不相关。

这就是协方差的意义。

 

 2.相关系数

　　就是协方差归一化：

　　　　

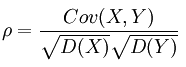
　　  D（X）和D（Y）代表X和Y的方差，方差意义是数值分布距离中心线的离散程度，那么协方差除以方差，不就等于去除了离散程度的影响吗？

 

 

 

知乎上一篇文章说的“协方差和相关系数”真是完美：https://www.zhihu.com/question/20852004 

此博文转载说的也很好：http://blog.csdn.net/wuhzossibility/article/details/8087863